Isosceles Right-angled Triangle
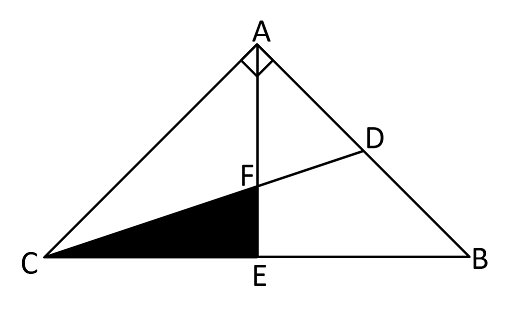
ABC is a right triangle as shown. Given that D is the midpoint of A B , E is the midpoint of B C , and the side lengths of A B and A C are both 12, find the area of the shaded region.
The answer is 12.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Very elegant proof ever! :)
Log in to reply
Agreed! Realizing that F is the centroid and that the triangle is 1/6 the area makes this really quick!
How can we know that F E = 3 A E ?
Oh, i forgot it.. Since F E = 2 A F , then F E = 3 A E . Nice solution!
Let H be a point on B C such that D H ⊥ C B . So we have △ A B C ∼ △ D B H ⇒ C H = 9 2 . And finally: △ H C D ∼ △ E C F ⇒ D F = 2 2 ⇒ A R E A E C D = 1 2
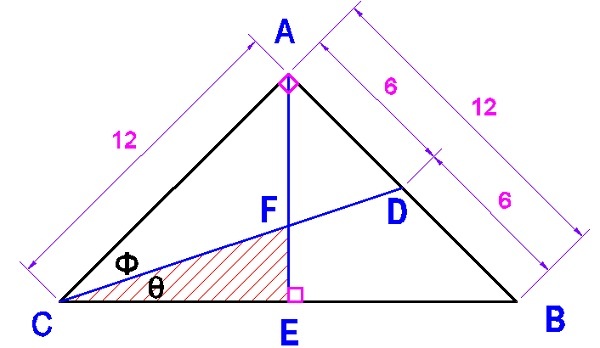 t
a
n
Φ
=
1
2
6
t
a
n
Φ
=
1
2
6
Φ = 2 6 . 5 6 5 0 5 1 1 8 °
θ = 4 5 ° − 2 6 . 5 6 5 0 5 1 1 8 ° = 1 8 . 4 3 4 9 4 8 8 2 °
C E = 2 1 2 2 + 1 2 2 = 2 2 8 8
t a n 1 8 . 4 3 4 9 4 8 8 2 ° = 2 2 8 8 F E
F E = 2 . 8 2 8 4 2 7 1 2 4
A s h a d e d = ½ ( 2 . 8 2 8 4 2 7 1 2 4 ∗ 2 2 8 8 ) = 1 2 c m 2
Draw median line from B that goes through F and intersects AC at G. So we divide triangle ABC into 6 smaller triangles with same area. Let the area of this triangle is x. We have 6x=72, x=12. Then the area of the shaded triangle is 12
Point F is a centroid of △ A B C therefore F E = 3 A E therefore △ C F E = 3 △ A E C . △ A E C = 2 △ A B C = 2 × 2 1 2 × 1 2 = 3 6 △ C F E = 3 △ A E C = 3 3 6 = 1 2
Note: Medians divide any triangle into 6 smaller triangles of equal areas.