Isosceles Triangle and a Peculiar Point D
A B C is an isosceles triangle with A B = A C , ∠ B A C = 9 6 ∘ . D is a point such that ∠ D C A = 4 8 ∘ , A D = B C and angle D A C is obtuse. What is the measure (in degrees) of ∠ D A C ?
The answer is 102.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
21 solutions
We may draw △ A B C and examine where the point D is located. Let E be the reflection of B across the midpoint of A C , and draw the circle centered at A with radius A E . Notice that A B C E is a parallelogram, so B C = A E . Therefore, D must be located on this circle. Also, we notice that if a point satisfies the conditions, the its reflection across A C must also satisfy them. Furthermore, since they are symmetric about A C , ∠ D A C must be the same for both of these points.
Without a loss of generality, let D and A be on the same side of B C . This means that ∠ B C D = 4 2 ∘ + 4 8 ∘ = 9 0 ∘ . Let the intersection of C D and A E be F . We know that C D ⊥ B C ⟹ C D ⊥ A E . Since △ A C E is isosceles, C F bisects A E . But this means that D F is both an altitude and a median, so A D = E D . Also, A D = A E , since they are both radii. Therefore, △ A E D is equilateral. Finally, we may compute:
∠ D A C = ∠ D A E + ∠ E A C A E ∥ B C ⟹ ∠ E A C = ∠ A C B ∠ D A E + ∠ A C B = 6 0 ∘ + 2 1 8 0 ∘ − 9 6 ∘ = 1 0 2 ∘ .
A subtle aspect of this problem, is that there are actually 2 possible points for the location of D ! However, this doesn't affect the value of ∠ D A C , since the points are "symmetric about A C ".
Solutions that assumed that ∠ D C A = 9 0 ∘ or is equal to 6 ∘ were marked partially correct.
Another common mistake made by students who used sine rule, was to not explain why ∠ A D C could not be 1 5 0 ∘ .
Great solution!
In triangle ADC apply sine rule
s i n 4 8 A D = s i n D A C
Apply sine rule for triangle ABC Since it is isosceles the other 2 angles are 42 each
s i n 9 6 B C = s i n 4 8 A C
Divide the above 2 equations and as AD=BC they cancel out
s i n 4 8 s i n 9 6 = s i n D 4 2 . -(1)
Sin 96 =2 sin 48 cos 48
Hence equation 1 becomes
2cos 48=sin 42/sin D
But sin 42 = cos 48
Hence sin D =1/2
Case 1 D=150
This cannot be as sum df angles in a triangle must be 180
Case 2 D=30
Hence A=180-(42+30)=102
(Note A triangle ADC could also have been constructed such that angle D is 6 degrees instead of 48 But after solving that we would get angle DAC to also be obtuse but angle BAC is already obtuse.since the sum of all angles on line DA must equal 180.the sum of just these 2 angles cannot be greater than 180.hence such a triangle cannot be formed and the above solution is the only one)
since AB=AC, angle ABC=ACB=42 consider triangle ADC,by sine rule, AC/ sin(ADC)=AD/sin(48) ->1 now consider triangle ABC,again by sine rule, AC/sin(42)=BC/sin(96) ->2 now divide equation 1 by 2 since AD=BC, we get sin(ADC)= (sin(48)sin(42))/sin(96)=1/2 this give ADC=30, from triangle ADC, DAC=180-30-48=102
Let angle ADC = x. By Sine Rule applied to triangle ADC, sin x / AC = sin 48 / AD ... (i). Triangle ABC is isosceles with angle BAC = 96 degres. So angle ABC = (180 - 96) / 2 = 42 degrees. Again by Sine Rule applied to triangle ABC, AC / sin 42 = BC / sin 96 ... (ii). Given AD = BC ... (iii). Multiply equations (i) and (ii) and use (iii) to obtain sin x / sin 42 = sin 48 / sin 96 RHS simplifies thus: sin 48 / 2 sin 48 cos 48 = 1 / 2 cos 48 = 1 / 2 cos(90 - 42) = 1 / 2 sin 42. Therefore sin x = 1 / 2 , angle ADC = x = 30 degrees. Already angle DCA = 48 degrees. Hence angle DAC = 180 - ( 30 + 48) = 102 degrees.
Since ABC is an isosceles triangle where AB=AC and angle BAC=96, angle ACB=angle ABC =42 [ sum of angles of a triangle is 180 and base angles of isosceles triangle are equal] Now, In triangle ABC, sin96 /BC =sin42/AC BC= sin 96 *AC /sin42...i
In triangle ADC, Let angle ADC be x then, sinx/AC = sin48/AD AD=sin48 * AC/sinx ....ii
BC =AD [given] sin 96 AC /sin42 = sin48 * AC/sinx [from i and ii] sinx = sin48 * sin42/sin96 sinx = sin(48) sin42/sin(2 48) sinx = sin48 * sin42/ (2 sin48 * cos48) sinx =sin42/{2* cos(90-42)} sinx =sin42/{2* sin42} sinx =1/2 x= 30 as angle ADC must be acute because angle DAC is obtuse Now, angle DAC =180 - 30-48 =102
Applying sine rule to △ A D C and △ A B C , and using A D = B C , A B = A C , we get
s i n ( 4 2 ) A B = s i n ( 9 6 ) A D , s i n ( ∠ A D C ) A B = s i n ( 4 8 ) A D .
Simplifying then equating yields s i n ( 9 6 ) s i n ( 4 2 ) = s i n ( 4 8 ) s i n ( ∠ A D C ) .
Using double angle formula and simplifying yields,
2 c o s ( 4 8 ) s i n ( 4 2 ) = s i n ( ∠ A D C ) ⇒ 2 s i n ( 4 2 ) s i n ( 4 2 ) = s i n ( ∠ A D C ) ⇒ ∠ A D C = 3 0 ∘ .
Therefore, since ADC is a triangle, ∠ D A C = 1 8 0 ∘ − 3 0 ∘ − 4 8 ∘ = 1 0 2 ∘ .
Let E be the symmetric point of A to line C D and F be the intersection of A E and C D , M be the midpoint of B C .
It is easy to see that A M is the angle bisector of ∠ B A C . We have ∠ B A C = 9 6 ∘ so ∠ M A C = 2 1 ⋅ 9 6 ∘ = 4 8 ∘ and ∠ M C A = 4 2 ∘ .
Because ∠ F C A = 4 8 ∘ so two triangles Δ M A C and Δ F C A are equivalent. Hence, A F = M C , but A F = 2 1 A E and M C = 2 1 B C so A E = B C . As the given condition, we have A D = B C so A D = A E . The triangle A D E has A D = D E and A D = A E leads to Δ A D E is equilateral triangle. So that ∠ D A F = 6 0 ∘ and because D A C is obtuse so ray A F lies between ray A D and ray A C , hence ∠ D A C = ∠ D A F + ∠ F A C = 6 0 ∘ + 4 2 ∘ = 1 0 2 ∘ .
Therefore, ∠ D A C = 1 0 2 ∘ .
Draw a triangle ABC with AB=AC. Let BC=2x. As given \angle ABC = 96 ^ \circ, therefore by angle sum property since A+B+C=180 degrees, and as angle B= angle C, this implies B+C=84 degrees or 2 \times B = 84 degrees or B=C=42 degrees. Now angle DCA= 48 degrees therefore D must lie outside the triangle because angle BCA=42 degrees is the maximum possible angle in the triangle. Thus angle(DCA + ACB)= \angle DCB = 90 ^ \circ . Now drop a perpendicular from A to BC, say AG. Since angle AGC = angle DCG = 90 degrees, this implies AG is parallel to CD. And since ABC is isosceles, this implies that BG=CG. Also if we drop a perpendicular from A to CD, and name it AQ, it results in the formation of the rectangle AQCG and therefore AQ=CG, however CG=BC/2= x, therefore AQ= x. As given AD=BC=2x, thus if we apply Pythagoras theorem to triangle AQD, AQ^2 + DQ^2 = AD^2, thus, x^2 + DQ^2 = 4x^2, i.e. DQ^2=3x^2 i.e. DQ=\sqrt{3}x. Now tan(ADQ) = AQ/DQ= x/\sqrt{3}x= 1/\sqrt{3} , this implies angle ADQ=30 degrees. But as AG is parallel to CD, thus angle GAC+CAD+ADC=180 degrees, or angle DAC+(48+30)degrees = 180 degrees, or angle DAC= (180-78) degrees = 102 degrees.
Suppose there exists a point E such that D and E are symmetrical about triangle ABC's axis of symmetry. Then, <EBD = 48 and AE = CB.
Note that <DCB = <DCA + <ACB = 48 + (1/2)(180 - <BAC) = 48 + 42 = 90 degrees. Similarly, <EBC = 90 degrees. Therefore, BCDE is a rectangle (by symmetry about ABC's axis), so DE = BC. Since AD = BC and AE = BC, triangle ADE is equilateral, so <DAE = 60. By symmetry:
<DAC = (1/2) * (360 - <BAC - <DAE) = (1/2) * (360 - 96 - 60) = 102 deg.
Let angle ADC=x. Then by Law of Sines on triangle ADC we have that sin 48/AD=sin x/AC. Using Law of Sines on triangle ABC gives sin 96/BC=sin 42/AC. Dividing the two equations and using AD=BC gives sin 48/sin 96=sin x/sin 42 Rearranging the terms and using that sin a= cos (90-a) gives sin x=cos 48 * sin 48/sin 96 which by the double angle formula means that sin x=1/2. So x=30 and angle CAD=102.
let us first try to locate the position of the point D.In isosceles triangle ABC \angle ABC = 42 ^\ circ. since \angle DCA = 48 ^\ circ. i.e angle DCA> angle ABC. clearly the point D will be on outside of the triangle actually on the right side of ABC. now triangle ACD is completed. applying sine rule in ABC we get; BC/sin\ 96^\ circ = AC/sin\ 42^ \ circ .................(1) again applying sine rule in ACD we get; AC/sin\ ADC\ =AD/sin\ 48^\circ .............(2) but given that AD=BC therefore BC/sin\ 48^\ circ =AC/sin\ ADC..................(3) dividing equation (1) by equation (2) we get; sin\ ADC\ /sin\ 42^\ circ = sin\ 48^\ circ/sin\ 96^\ circ = sin\486\ circ /cos\ 6^\ circ . or sin\ angle ADC= \frac {1}{2} [2(sin\ 42)(sin\ 48)]/ cos\ 6\ thus sin\ angle ADC = \frac {1}{2} or \angle ADC = 30^. therefore \angle DAC = (180-(30+48)^\ = 102^.
First, let's understand the point D . The conditions ∠ D C A and A D = B C are the intersection of a line with a circle, which gives 2 points. The condition that ∠ D A C is obtuse then removes the ambiguity, making D the further point of intersection.
Since A B C is an isosceles triangle and ∠ B A C = 9 6 ∘ , we have ∠ A C B = 2 1 8 0 ∘ − 9 6 ∘ = 4 2 ∘ . We have ∠ D C B = ∠ D C A + ∠ A C B = 4 8 ∘ + 4 2 ∘ = 9 0 ∘ . Let E be the point such that B C D E is a rectangle. A is the perpendicular bisector of B C , and hence D E , so A D = A E . With the condition that A D = B C = D E , we see that A D E is an equilateral triangle. Thus, ∠ A D E = 6 0 ∘ , ∠ A D C = 3 0 ∘ .
Hence ∠ D A C = 1 8 0 ∘ − ∠ A D C − ∠ A C D = 1 8 0 ∘ − 3 0 ∘ − 4 8 ∘ = 1 0 2 ∘ .
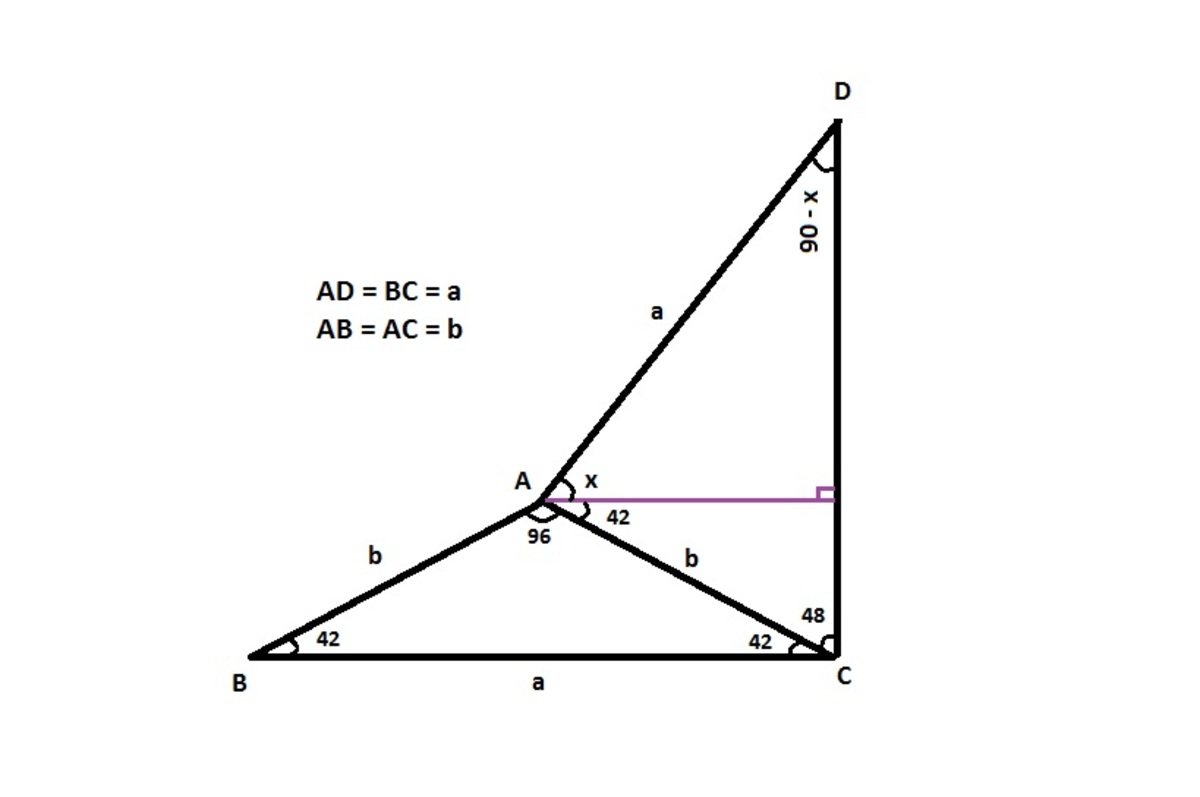
Using the sine rule, we get:
For Δ A B C , a sin 9 6 o = b sin 4 2 o
For Δ A C D , a sin 4 8 o = b sin ( 9 0 − x ) o
a b = sin 9 6 o sin 4 2 o = sin 4 8 sin ( 9 0 − x ) o
→ cos x = sin 9 6 o sin 4 2 o × sin 4 8
→ x = 6 0 o
→ ∠ D A C = 6 0 0 + 4 2 o = 1 0 2 o
 Make M such that AM is perpendicular to BC.
Make I such that AI is perpendicular to CD
Then angle DAI is 60 degress because IA/AD = cos(DAI) = 1/2
Also, angle IAC = ACB = 42 ( Isocles triangle)
So, angle DAC = 60 + 42 = 102//
Make M such that AM is perpendicular to BC.
Make I such that AI is perpendicular to CD
Then angle DAI is 60 degress because IA/AD = cos(DAI) = 1/2
Also, angle IAC = ACB = 42 ( Isocles triangle)
So, angle DAC = 60 + 42 = 102//
Draw the figure first, and then draw a line A E such that A E = A D = B C , ∠ D A C = ∠ E A C , and ∠ E B A = ∠ D C A = 4 8 ∘ . Now, ∠ B C A = ∠ A B C = 4 2 ∘ , so ∠ D C B = ∠ E B C = 9 0 ∘ . By A S A on sides A B , A C , and angles ∠ E A C , ∠ D A C , ∠ E B A , and ∠ D C A , △ E A C is congruent to △ D A C , so E B = D C and B C D E is a rectangle. Thus, B C = D E and △ A D E is equilateral, so ∠ A D C = 3 0 ∘ , and, finally, ∠ D A C = 1 8 0 ∘ − 3 0 ∘ − 4 8 ∘ = 1 0 2 ∘ .
Let AE perpendicular to CD,E is the foot of perpendicular.Since angle BCD is right angle,AE is parallel to BC,indicating that angle CAE=angle ACB=48 degrees.Since triangle ABC is isosceles, obviously AE is half of the length of the base BC. Hence cos DAE=AE/AD=AE/BC=0.5BC/BC=0.5.So angle DAE=60 degrees. This, angle DAC=angle DAE+angle EAC=42+60=102. Thank you for spending time reading my solution.
Here is my solution,
Draw CX such that CX=AC, and angle DCX=48 degrees.
Then triangle ACX is congruent to ABC. So we have AX=BC=AD. Again we have CD as angle bisector of angle XCA, and ACX isosceles, so CD is perpendicular to AX and bisects AX at K (say). Now KDX and KDA are congruent triangles by SAS, ( right angle at K, AK=KX, KD common) so AD=DX, and by construction AD=AX.
So ADX is equilateral. angle DAC=60+angle XAC=60+42=102.
Hence Q.E.D.
We can solve it by issuing the sine rule. Let AB=AC=x and BC=AD=y.
In triangle ABC, x/sin96 = y/sin42.
So x=ysin96/sin42= 2y sin48 cos48/sin42=2ysin48. (As sin42=cos48).
In DAC, x/sin48=y/sin(k). (K=angle ADC)
Replacing x in equation, we get sin(k)=0.5. So k=30 degrees. So angle DAC= 180-30-48=102 degrees.
Let E be the point so, B , C , E colinear and C E = A C . Since ∠ D C B = 9 0 ∘ , we have ∠ D C E = 9 0 ∘ . Hence, ∠ C A E = ∠ A E C = 2 1 ∘ .
Now, trace a line from point A parallel towards B C , and let F be the points, that A F / / B C . Since A F / / B C , B E / / A F , then ∠ E A F = ∠ A E B = 2 1 ∘ .
Look that C D and A F intersects, let it G . Since Δ A B C is isosceles triangle and the height of Δ A B C is definitely parallel to C D , A G = 2 1 B C . Note that G F = A G , which makes F D = F A = B C . Thus, ∠ A F D is an equilateral triangle. Hence, ∠ F A D = 6 0 ∘ . Finally, ∠ D A C = ( 2 1 + 2 1 + 6 0 ) ∘ = 1 0 2 ∘
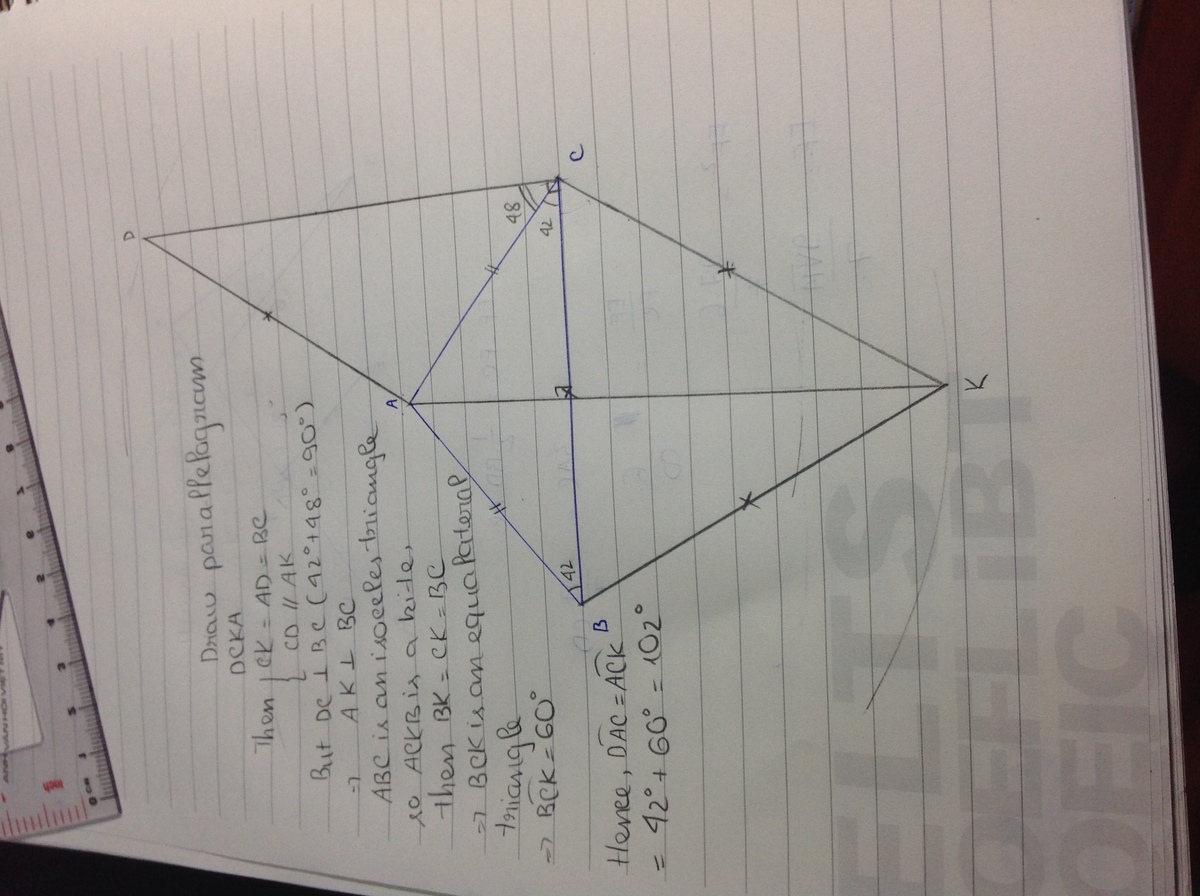
Let a = B C and b = A C = A B . Also, let the altitude from A intersect B C at point H . Because △ A B C is isosceles, this altitude is also a median, so H is the midpoint of B C . Therefore, C H = 2 a . Furthermore, because △ A B C is isosceles, A H is the angle bisector of ∠ B A C , so ∠ C A H = 2 9 6 ∘ = 4 8 ∘ . Thus, sin 4 8 ∘ = A C C H = b 2 a = 2 b a .
In △ A C D , A D = B C = a and A C = b . By Law of Sines, we have a sin 4 8 ∘ = b sin ∠ A D C ⟹ a 2 b a = b sin ∠ A D C ⟹ sin ∠ A D C = 2 1 . The only solutions where ∠ A D C < 1 8 0 ∘ are ∠ A D C = 3 0 ∘ and ∠ A D C = 1 5 0 ∘ . In the first case, we have ∠ D A C = 1 8 0 ∘ − ∠ A C D − ∠ A D C = 1 8 0 ∘ − 4 8 ∘ − 3 0 ∘ = 1 0 2 ∘ . Note that in this case, ∠ D A C is obtuse. The second case is impossible, since ∠ D A C + ∠ A C D + ∠ A D C = ∠ D A C + 4 8 ∘ + 1 5 0 ∘ > 1 8 0 ∘ . Thus the only solution is ∠ D A C = 1 0 2 ∘ .