Isosceles Triangle in a Square
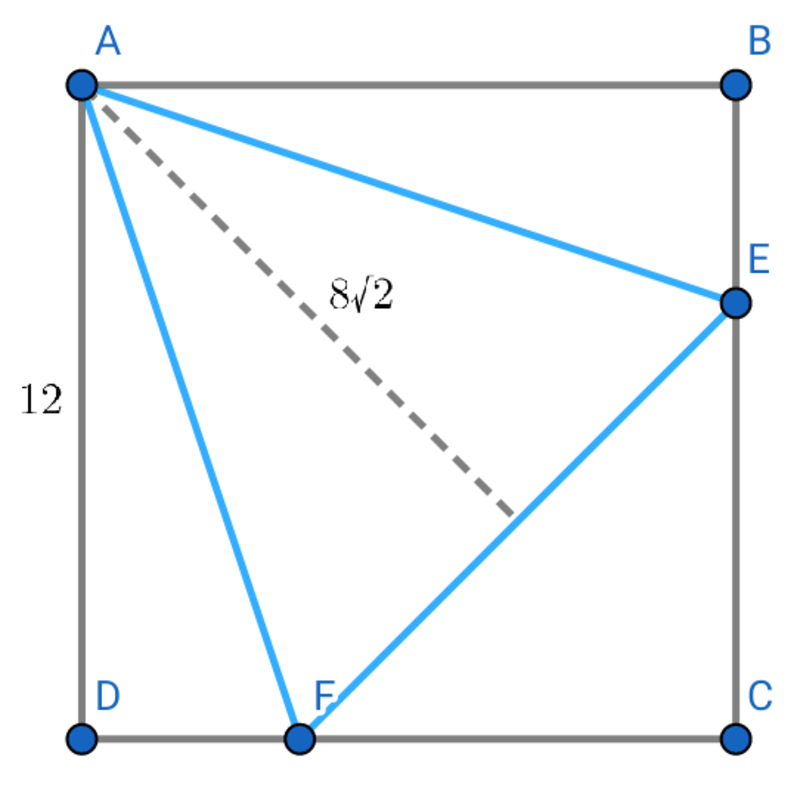
Isosceles △ A E F of height 8 2 and A E = A F is inscribed in square A B C D of side length 1 2 , where it shares a common vertex A .
What is the area of △ A E F ?
The answer is 64.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Interesting approach.. +1
But how can you say that CE = CF.
Log in to reply
△ A B E and △ A D F are similar. Therefore, B E = D F and C E = C F .
Why are going for lengthy to find triangle 🔺️ area. You can go as 1/2(8 root2) ( 8 root 2)= 64
Let the foot of perpendicular from A to F E be G . Then ∣ A G ∣ = 8 2 , ∣ A C ∣ = 1 2 2 , ∠ A C D = 4 5 ° ⟹ ∣ G C ∣ = ∣ G F ∣ = 4 2
Hence the area of △ A E F is 4 2 × 8 2 = 6 4 square units.
IMHO there is a much simpler way of solving this. WARNING: very basic math ahead
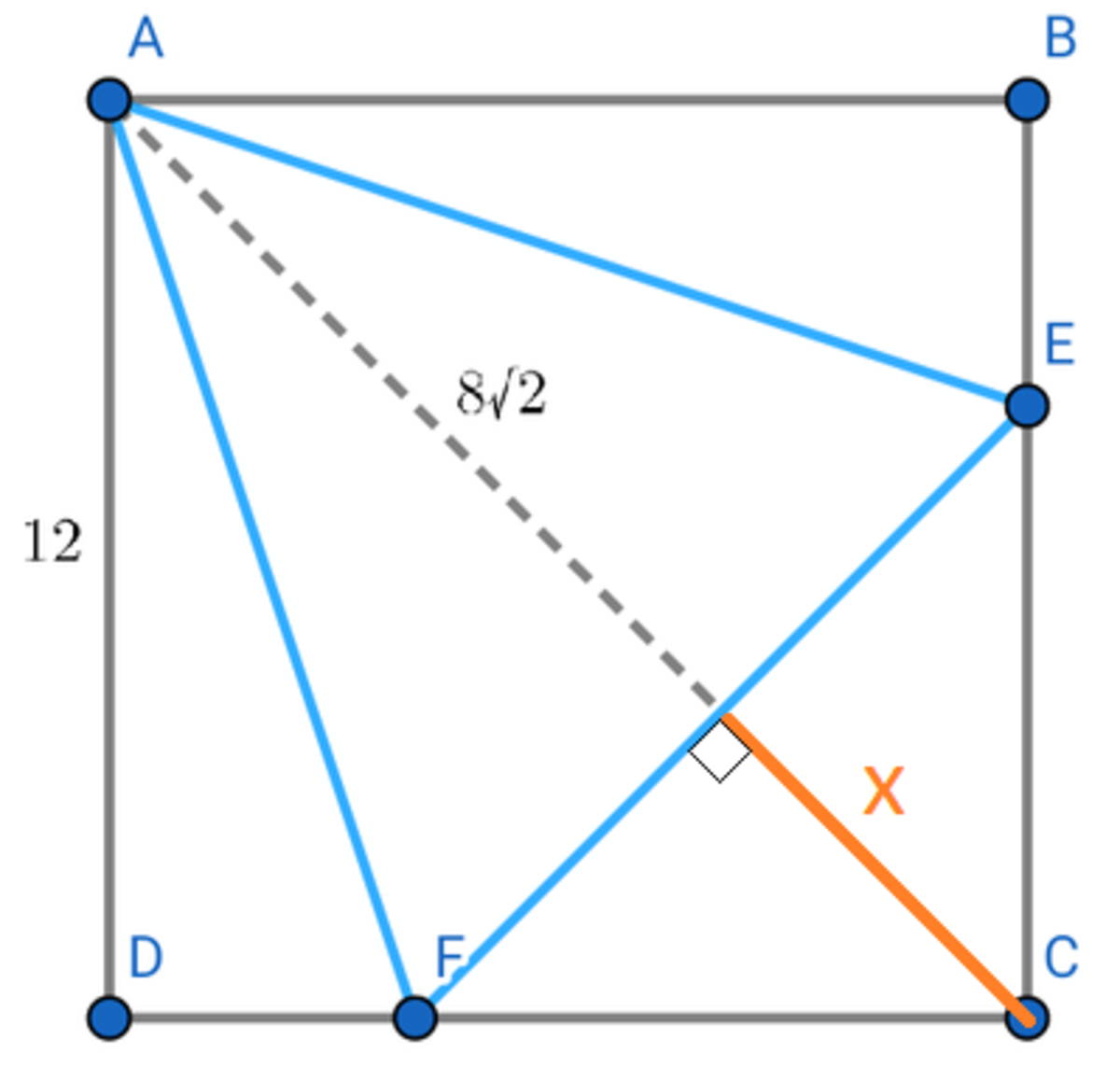
Since E F is normal to A C we can solve for x (= 2 E F ) by via:
x = 2 × 1 2 2 − 8 × 2
and then x × 8 × 2 = A
Let D E = x , then using pythagorean theorem twice, we get:
( 2 2 ( 1 2 − x ) 2 ) 2 + ( 8 2 ) 2 = ( x 2 + 1 2 2 ) 2
Solving and simplifying this, and rejecting the negative solution, we have x = 4 . Then:
E F = 2 ( 1 2 − 4 ) 2 = 8 2
Now, the area of triangle an be found easily
[ △ A E F ] = 2 1 8 2 ⋅ 8 2 = 6 4
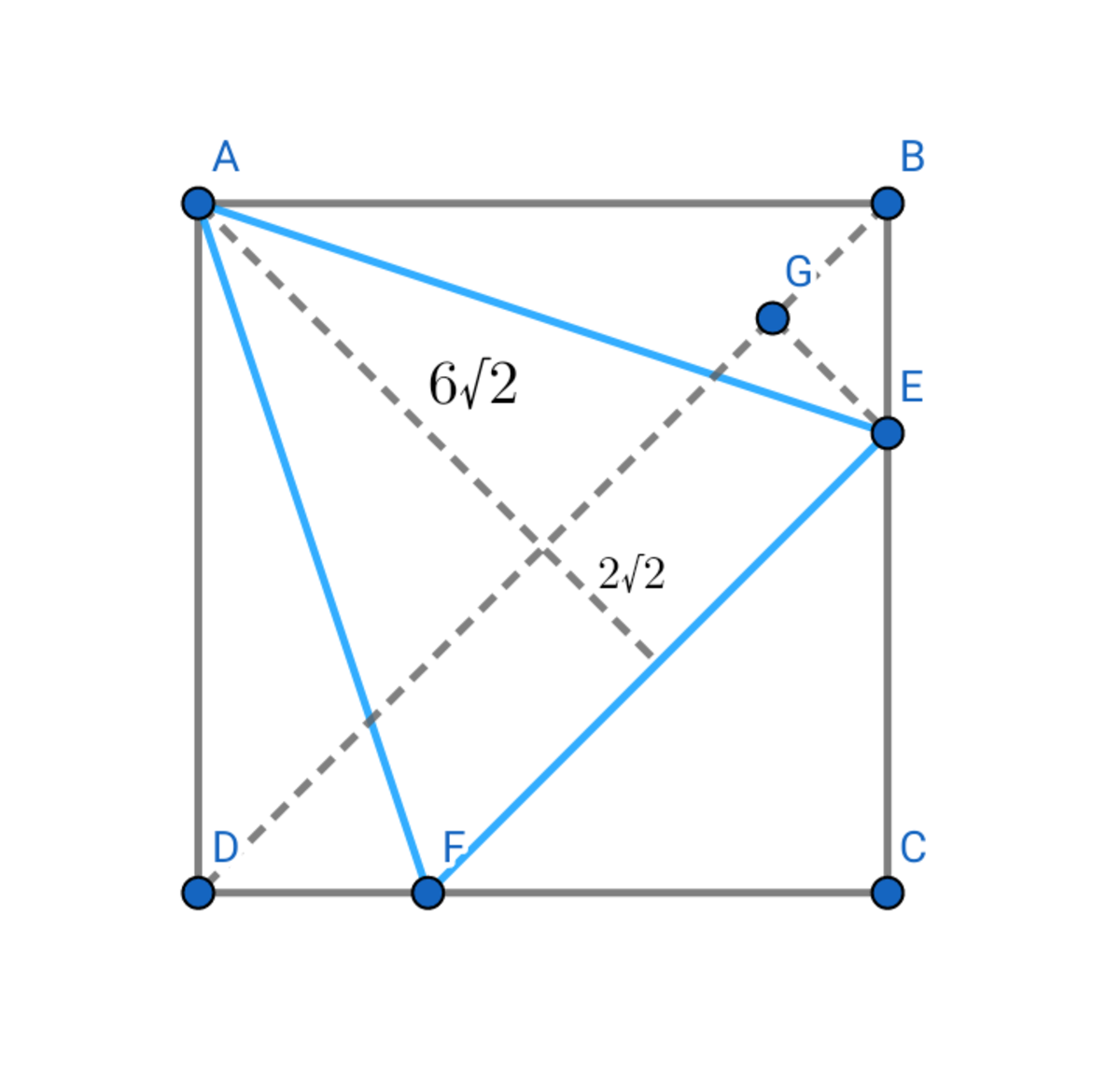
Diagonal B D is parallel to line segment F E and is the base of △ D C B . Triangle D C B and triangle C F E are similar triangles. Meaning, according to a Similar Triangles Theorem , D F D B = D E D C = E F C B . The height of the isosceles triangle is equal to the sum of half of the square's diagonal and the distance between C D and F E .
2 1 2 2 − 8 2 = 2 2 ⟹ The distance between C D and F E = G E
We can now get the leg lengths of △ D F E , figure out the length of F E , and finally compute for the area of the isosceles triangle.
F D = F D = F D = F D = F D = B D − B F 1 2 − sin 4 5 ∘ G E 1 2 − sin 4 5 ∘ 2 2 1 2 − 4 8
Next, with the equation 8 1 2 = F E 1 2 2 , line segment F E is 8 2 . We can now compute for the needed area: 2 ( 8 2 ) 2 = 6 4 .
@Kaizen Cyrus , you have to mention A E = A F in your problem. Isosceles can mean A E = E F or A F = E F .
I stated in the previous edit of the problem that the vertex angle of said triangle is at ∠ A .
Log in to reply
Sorry, I didn't know what a vertex angle is. I edited your problem. It is clearer this way.
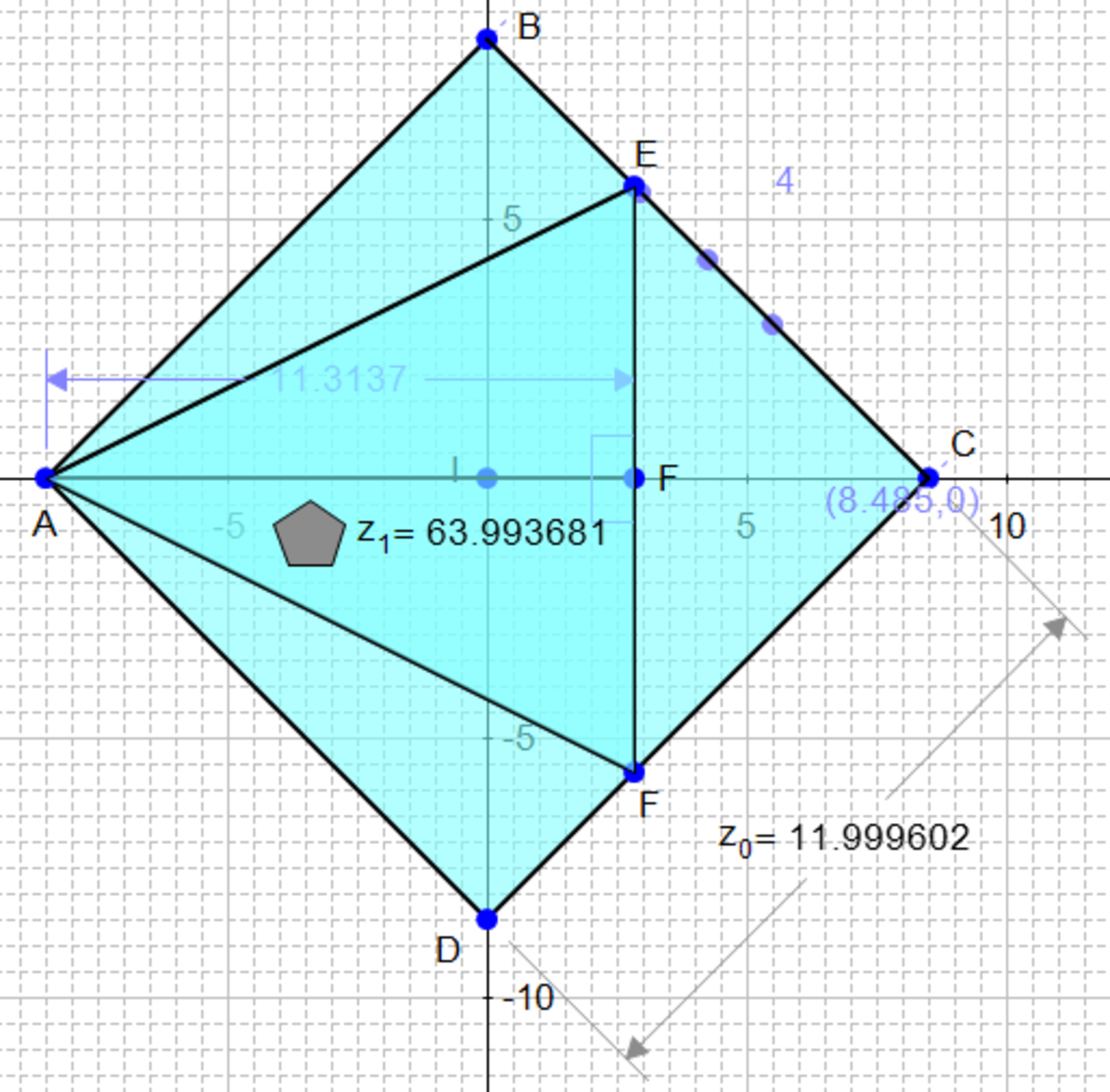
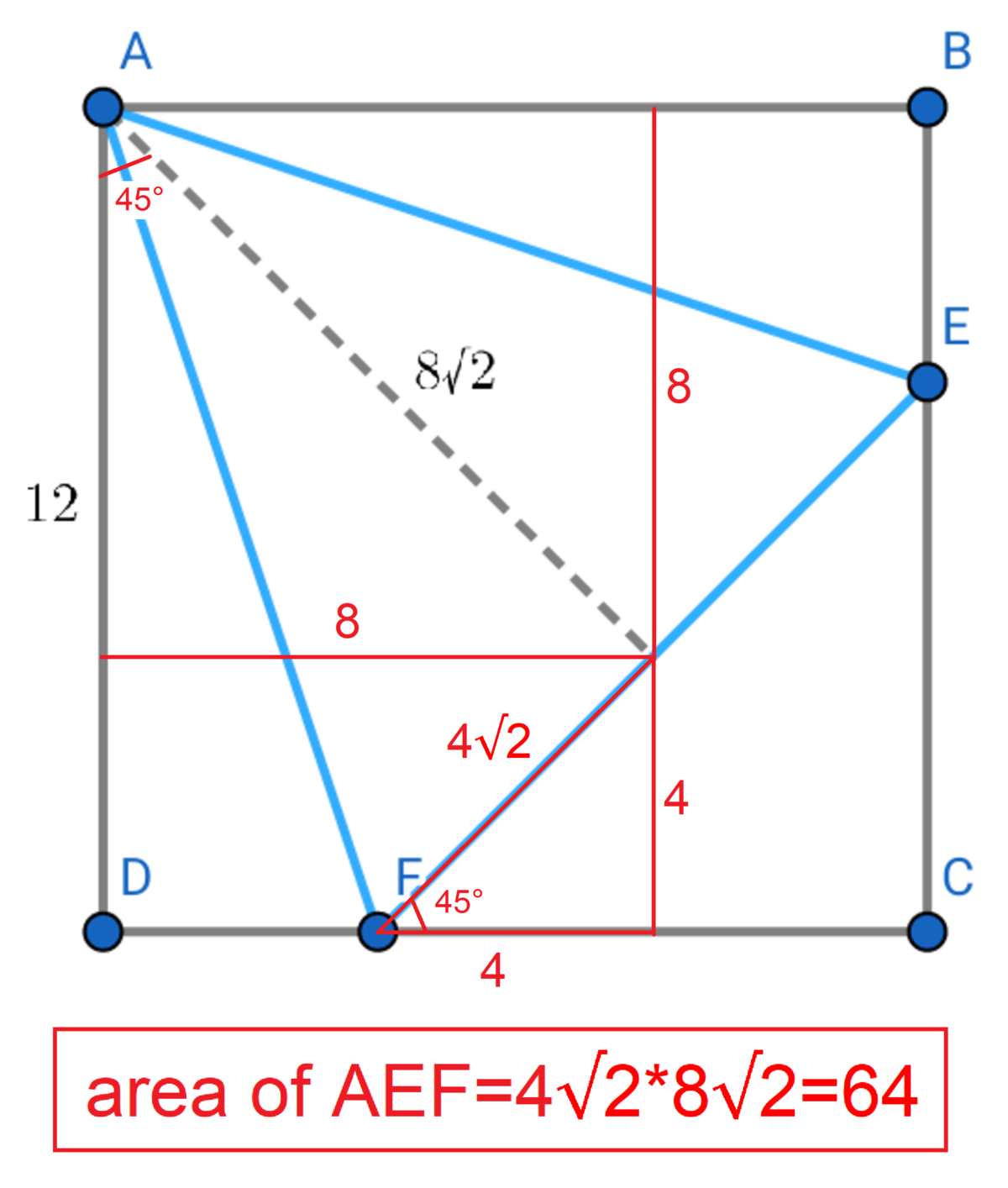
If we extend the altitude of the isosceles △ A E F , we find that it is part of the diagonal A C of length 1 2 2 . If we draw a square with C E and C F as two of the sides, we find that square A ′ E C F has a diagonal A ′ C of length 8 2 . Since A C A ′ C = 1 2 2 8 2 = 3 2 , this means that C E = C F = 3 2 A B = 8 , ⟹ B E = D F = 4 . Then the area of △ A E F , [ A E F ] = [ A B C D ] − [ A B E ] − [ A D F ] − [ C E F ] = 1 4 4 − 2 4 − 2 4 − 3 2 = 6 4 .