Isosceles triangle length

Geometry Level 1

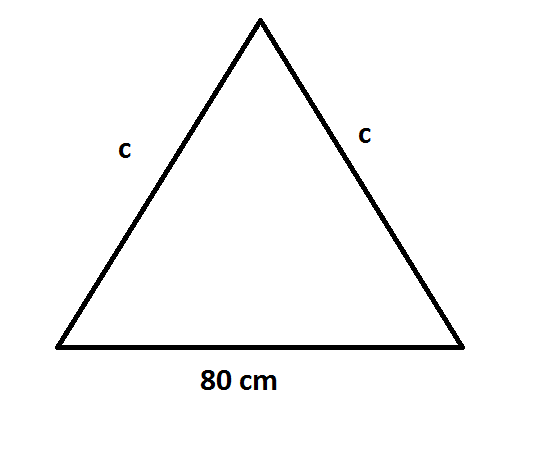
Above is a isosceles triangle. Which have an area of 3000 cm 2 \text{cm}^2 . Find c c


The answer is 85.

Munem Shahriar by Munem Shahriar , 18, Bangladesh

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Munem Shahriar
Feb 3, 2018

The area of the isosceles triangle is b 4 4 c 2 − b 2 \dfrac b4 \sqrt{4c^2 - b^2} , where b = 80 cm b = 80 \text{cm} .

b 4 4 c 2 − b 2 = 3000 80 4 4 c 2 − 8 0 2 = 3000 20 4 c 2 − 8 0 2 = 3000 4 c 2 − 8 0 2 = 150 ( 4 c 2 − 6400 ) 2 = ( 150 ) 2 [ Square on both sides ] 4 c 2 − 6400 = 22500 4 c 2 = 28900 c 2 = 7225 ⟹ c = 85 \begin{aligned} \dfrac b4 \sqrt{4c^2 - b^2} & = 3000 \\ \dfrac{80}{4} \sqrt{4c^2 - 80^2} & = 3000 \\ 20 \sqrt{4c^2 - 80^2} & = 3000 \\ \sqrt{4c^2 - 80^2} & = 150 \\ (\sqrt{4c^2 - 6400})^2 & = (150)^2 ~~~~~~~~~~~~ [\text{Square on both sides}] \\ 4c^2 - 6400 & = 22500 \\ 4c^2 & = 28900 \\ c^2 & = 7225 \\ \implies c&=\boxed{85} \\ \end{aligned}

3 Helpful 1 Interesting 0 Brilliant 0 Confused

You can get the answer in 2 steps. Draw a median from A to BC. Since, it is an isosceles triangle, the median is also the perpendicular bisector. Using half base into height formula, find the height. After that, use pythagoras theorem to find c.

A Former Brilliant Member - 3 years, 4 months ago
Mahdi Raza
May 4, 2020

1 2 b h = 3000 ⟹ h = 75 \frac{1}{2}bh = 3000 \implies h = 75 . By Pythagorean theorem: c 2 = 7 5 2 + 4 0 2 c^2 = 75^2 + 40^2 ⟹ c = 85 \implies \boxed{c = 85}

1 Helpful 1 Interesting 1 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...