Isosceles Triangle?

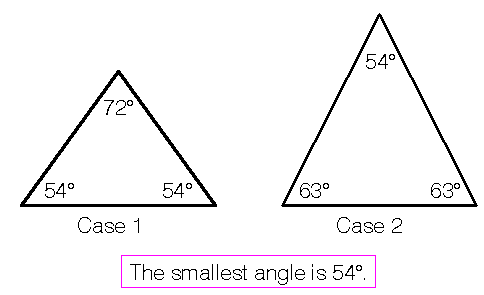
Case 1: When $54^{\circ}$ is the angle which is not equal to any of the two other angles

Then, let the equal angles be $x$ . We have from the angle sum property:

$x + x + 54^{\circ} = 180^{\circ} \implies \boxed{x = 63^{\circ}}$

Therefore, the angles of the triangle are $54^{\circ}$ , $63^{\circ}$ and $63^{\circ}$ .

Case 2: When $54^{\circ}$ is one of the angles equal to another angle of the triangle

Then let the other angle be $x$ . We again have from the angle sum property:

$54^{\circ} + 54^{\circ} + x = 180^{\circ} \implies \boxed{x=72^{\circ}}$

In this case, the angles of the triangle are $54^{\circ}$ , $54^{\circ}$ and $72^{\circ}$ .

In both the cases, $54^{\circ}$ is the smallest angle of the triangle, which has not been included in the options. So, None of these is the most appropriate option here.

It's obviously None of these because it says one of the angles it is 54, and the answers are 63 and 72, so you can infer that the answer is none of these.

One of the angles of an isosceles triangle is $54^{\circ}$ , Since no other options is not less than 54 degrees, the answer is none of these .

This should be in Logic, not Geometry. Both options shown are values higher than 54 degrees, so the answer is "None of these."