All Triangles Are Isosceles

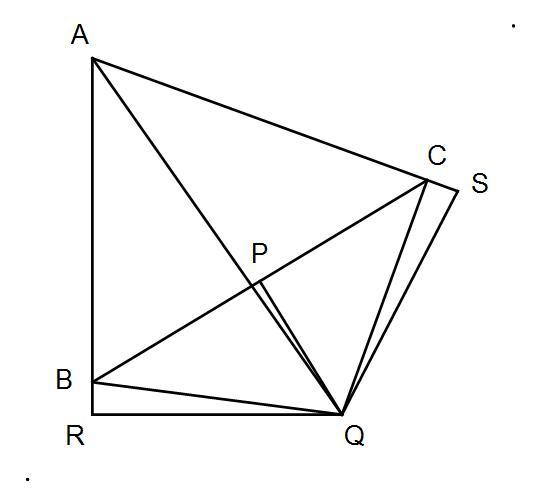
Let $\Delta ABC$ be an arbitrary triangle.

Point $P$ is the midpoint of line $BC$ , and line $PQ$ is perpendicular to line $BC$ .

Line $AQ$ bisects angle $\angle BAC$ .

Lines $AB$ and $AC$ are extended as necessary to include points $R$ and $S$ such that $\Delta AQR$ and $\Delta AQS$ are right triangles.

By reason of symmetry, line segments $BQ$ and $CQ$ are equal.

By reason of symmetry, line segments $RQ$ and $SQ$ are equal.

Therefore, by reason of congruent right triangles, line segments $BR$ and $CS$ are equal.

But, also by reason of congruent right triangles, line segments $AR$ and $AS$ are also equal.

Therefore, line segments $AB$ and $AC$ are equal, and triangle $\Delta ABC$ is isosceles.

Which of the following multiple choice answers is correct?

---

Note : This problem is a refugee from Brilliant April Fools' Day