Isosceles triangles

Geometry Level pending

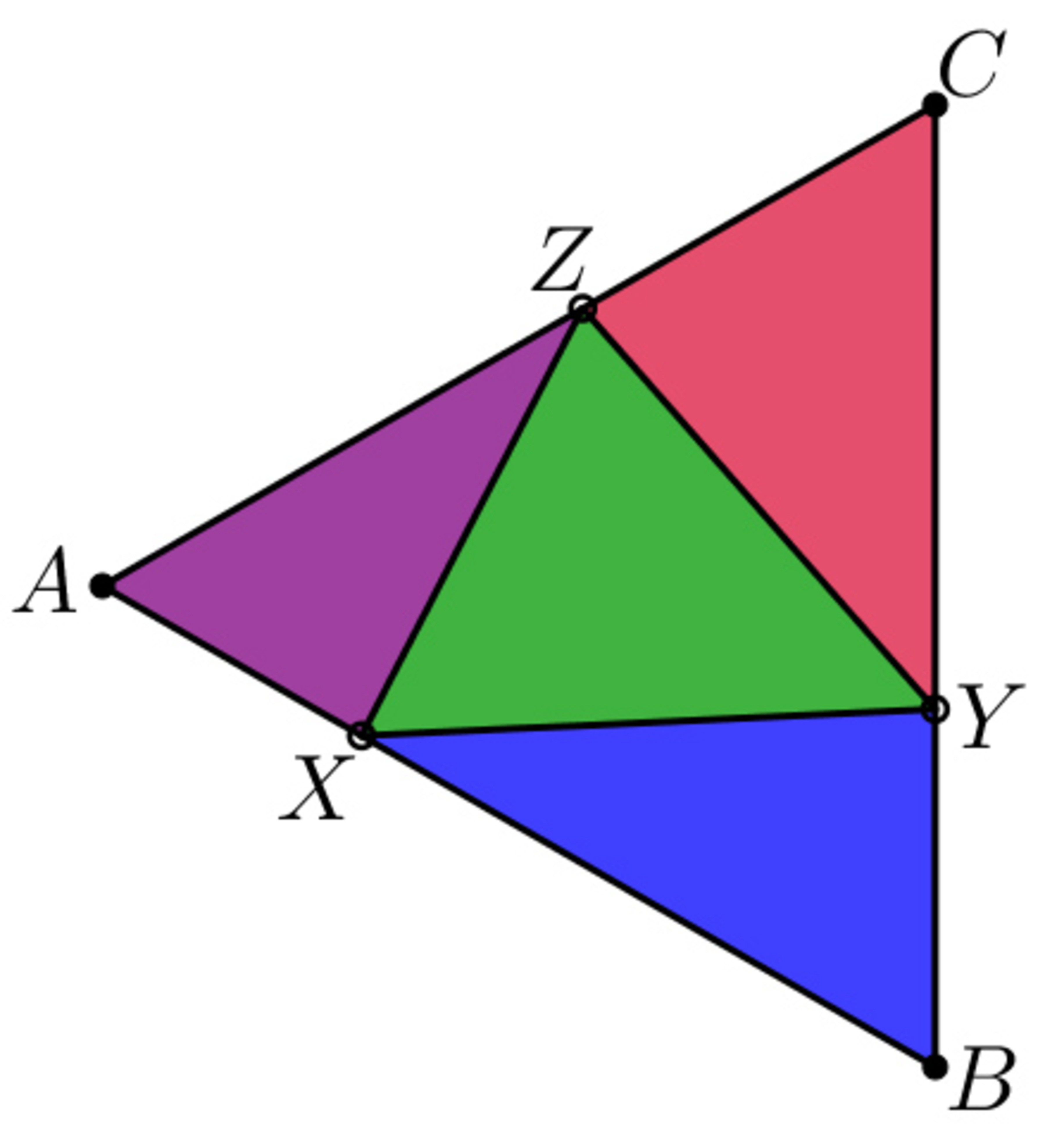
The A B C ABC triangle is equilateral. The X , Y , Z X, Y, Z points are respectively on the A B , B C , C D AB, BC, CD sides. We know that there are exactly n n isosceles triangle from the A X Z , X B Y , C Z Y , X Y Z AXZ, XBY, CZY, XYZ triangles. How many possible values are there for n n ?

This problem is from the "Kalmár László" Hungarian maths competition.
5 1 2 0 4 3

Áron Bán-Szabó by Áron Bán-Szabó , 17, Hungary

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Marta Reece
May 21, 2017

To prove existence of a the divisions with a given number of isosceles triangles, all we have to do is show an example with that number, as is done above for numbers 4, 2, 1, and 0.

What is left is to prove non-existence of a division with exactly 3 isosceles triangles. At least two of these would have to be triangles with one of their vertices being A, B, or C. That means they would have to have at least one 6 0 ∘ 60^\circ angle, but an isosceles triangle with one angle 6 0 ∘ 60^\circ is an equilateral triangle. They could not be the same size, otherwise all the triangles would become the same and there would be 4 triangles, not 3.

This means that the third one could not be also in a corner, as that one has to have two different sides next to a 6 0 ∘ 60^\circ angle, so will not be isosceles. But the triangle XYZ will also have a 6 0 ∘ 60^\circ angle, because one of its vertices will be between the two equilateral triangles, and also would have to have two different size sides making up that angle.

So there are only 4 possibilities - 0, 1, 2, and 4.

1 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...