Issac's points

Geometry Level 3

There exists $2$ points on Cartesian coordinate. Point $B$ has coordinates $(0,1)$ . Point $A$ is on the origin $(0,0)$ .

Point $A$ and $B$ always has a constant distance of $1$ from each other.

Point $B$ moves with a horizontal velocity (parallel to the x-axis) of $v.$

Point $A$ moves with a horizontal velocity of $2v.$

Point $A$ 's vertical velocity (parallel to the y-axis) is $0$ while Point $B$ is allowed to move vertically in order to keep the constant distance of $1$ .

All this movement is happening in the first quadrant.

Let $P$ be the area made by the figure defined by: the $x$ axis, the $y$ axis, and the path traveled by point $B$ up to where it meets the $x$ axis. Find $\left\lfloor 1000P \right\rfloor .$

After you solve this, you might want to try a continuation of this problem.

Try my Other Problems

The answer is 785.

2 solutions

Mayank Singh
Feb 6, 2015

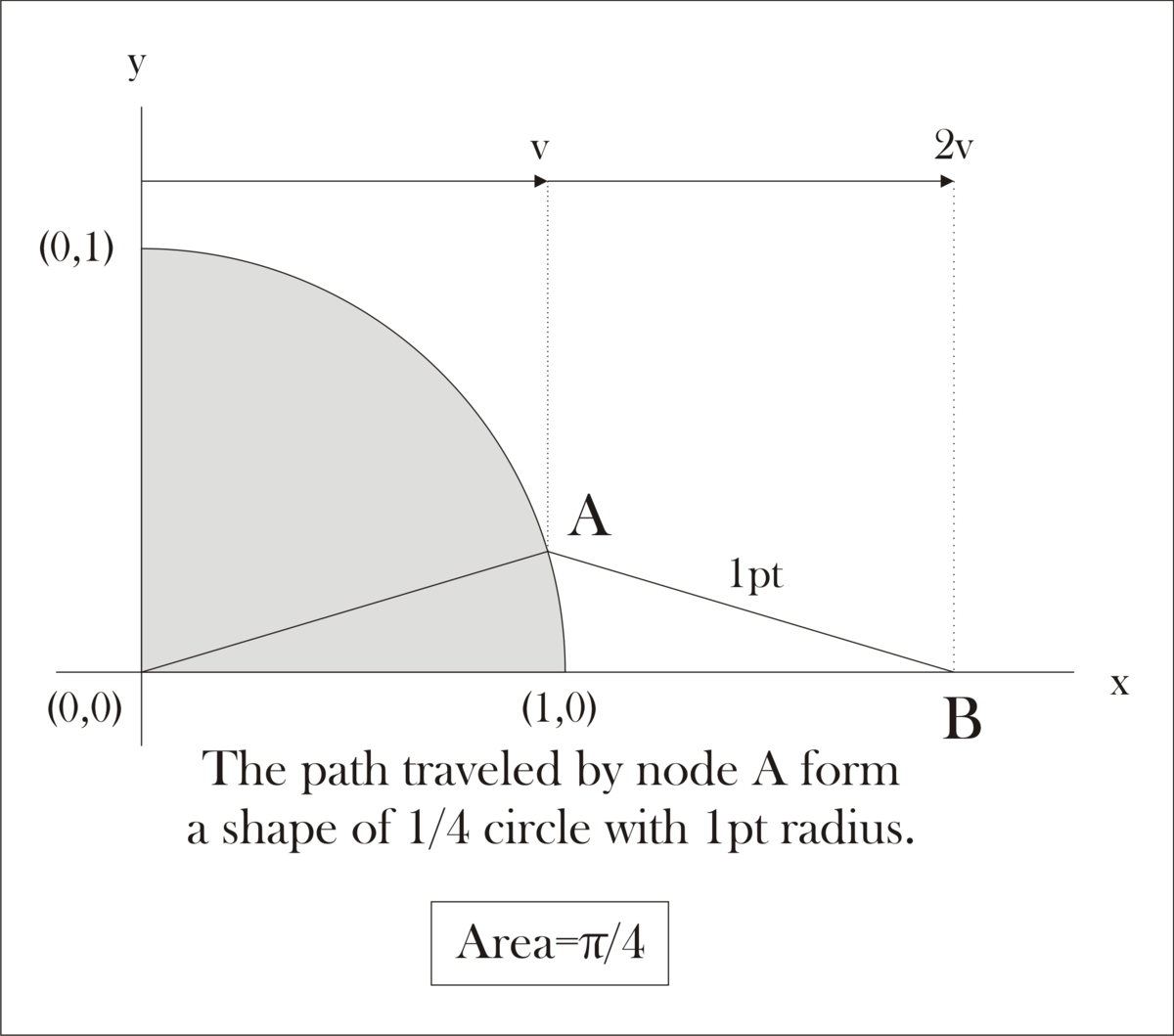
let coordinates of A at time $t$ be $(vt,y)$ and those of B $(2vt,0)$

Use distance formula to get $y$ , $y=\sqrt{1-v^2t^2}$

Hence locus of A is $x^2+y^2=1$

Area is $\frac{\pi}{4}$

Edited $LaTeX$ in your solution, you may use this for future references. You may also use simple Pythagoras theorem for getting y.

Pranjal Jain - 6 years, 4 months ago

@Julian Poon this is a beautiful problem!

Daniel Liu - 6 years, 4 months ago

Thanks! __

Julian Poon - 6 years, 4 months ago

Also, could we do this using Calculus or Vectors?

User 123 - 6 years, 4 months ago

You have interchanged A and B.referring to problem Is velocity of B always in horizontal direction?it must be in the direction of it's path.so coordinate of B cannot be (vt,y)

Navin Murarka - 3 years, 7 months ago

Horisadi Afyama
Feb 8, 2015

Point B is allowed to move vertically , not point A, so I think that this solution is not good.

Dorina Popescu - 1 year, 4 months ago

Issac's points

The answer is 785.

2 solutions

1 pending report

Vote up reports you agree with