It All Came From Pencils 3
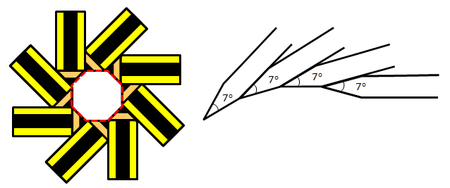 We can make "
pencilogons
" by aligning multiple, identical pencils end-of-tip to start-of-tip together without leaving any gaps, as shown above, so that the enclosed area forms a regular polygon (the example above left is an 8-
pencilogon
).
We can make "
pencilogons
" by aligning multiple, identical pencils end-of-tip to start-of-tip together without leaving any gaps, as shown above, so that the enclosed area forms a regular polygon (the example above left is an 8-
pencilogon
).
Hazri wants to make an n - pencilogon using n identical pencils with pencil tips of angle 7 ∘ . After he aligns n − 1 8 pencils, he finds out the gap between the two ends is too small to fit in another pencil.
So, in order to complete the pencilogon , he has to sharpen all the n pencils so that the angle of all the pencil tips becomes ( 7 − m ) ∘ .
Find the value of m + n .
(Assume the pencils have a rectangular body and have their tips resembling isosceles triangles)
The answer is 121.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
The question should write "after he aligned n-18 pencils, he found out the gap between the two ends is too small to fit in another pencil".
I want turkish language support. Because we don't understand this question.
Pleaseeeeeeeeeeeee turkish language support
I think it's safe to assume that given how a pencil sharpener works, each pencil has an isosceles triangle at the end, and then a rectangle for the rest of it. So the interior angle of the attempted pencilogon = 3 6 0 − 7 − 2 1 8 0 − 7 − 9 0 = 1 7 6 . 5 . Were this x-pencilogon to be completed, the sum of its interior angles would be: 1 7 6 . 5 x = ( x − 2 ) 1 8 0 ⇒ x = 1 0 2 . 8 5 7 To translate for the word problem, Hazri put down 102 pencils and found that there was not enough room to put down pencil 103. n − 1 8 = 1 0 2 ⇒ n = 1 2 0 Now one simply works backwards to find what the angle of the pencil should be to make this 120-pencilogon: Interior angle of the 120-pencilogon = 1 2 0 ( 1 2 0 − 2 ) 1 8 0 = 1 7 7 Let y be the interior angle of the sharpened pencil. Interior angle of the 120-pencilgon = 1 7 7 = 3 6 0 − y − 2 1 8 0 − y − 9 0 ⇒ y = 6 = 7 − m ⇒ m = 1 m + n = 1 2 1 □
The adjoining line of an n-gon takes a 360/n degrees turn. That is the turn centerlines of the pencils take.
Assuming pencil tip as isosceles triangle, its tip will be 2 * 360/n degrees.
So with tip of 7, the pencilogon will need
2
7
3
6
0
=
1
0
2
.
8
5
7
pencil. Therefore the pencils he has are n=102+18=120.
Thus the pencil angle must be 2*{360/120}=6. Implies m=7-6=1. Therefore m+n=121.
This made no sense!!! Maths is cancer!!!
In the triangle formed at the apex / tip, the two base angles sum are equal and sum upto 180-7 = 173. Thus each angle is equal to 173/2 = 86.5 . We need to compute each interior angle of the polygon. Int angle = 360 - (90 (from the cross-section of pencil) + 86.5 + 7) = 360 - 183.5 = 176.5.
Now we can estimate number of sides from the formula : Int angle of n-sided polygon = 180 - (360/n1) Therefore, 360 / n1 = 180 - 176.5 = 3.5 n1 = 360/3.5 = 102.86 which is not obviously not possible which indicates that the process of forming the polygon would have stopped here. Thus the original n = 102 (the floor of the above function) + 18 = 120 (which also seems to be the only feasible candidate .near 102 for getting an integral number of sides)
Now , the new interior angle = 180 - 360/120 = 180 - 3 = 177.
If the apex angle is x,
(180-x)/2 + 90 + x = 360-177 = 183
90 - x/2 + 90 + x = 183
180 + x/2 = 183
x/2 = 3
x = 6
7-m = 6 m = 1 n = 120
Therefore, m + n = 121
Suppose the angle of the pencil tips are x , it's not hard to show that the interior angles of the polygon ( pencilogon ) are 1 8 0 ∘ − 2 x . The exterior angles of the polygon are 1 8 0 ∘ − ( 1 8 0 ∘ − 2 x ) = 2 x .
Let's consider the situation when the pencils are not yet sharpened.
For all polygons, the sum of all exterior angles is always 3 6 0 ∘ , but in this case, since there are gaps, the sum of the exterior angles must be smaller than 3 6 0 ∘ , so 2 x ( n − 1 8 ) < 3 6 0 ∘ ⟹ ( n − 1 8 ) < x 7 2 0 ∘ . Here, x = 7 ∘ , so, ( n − 1 8 ) < 7 7 2 0 ∴ n < 1 2 0 7 6 Thus, we know that Hazri originally wants to make a 120- pencilogon , n = 1 2 0 (If n < 1 2 0 , then the gap would be large enough to fit at least 1 pencil, which is not what we wanted).
A 120- pencilogon has exterior angles of 1 8 0 ∘ − 1 2 0 1 1 8 × 1 8 0 ∘ = 3 ∘ , after he had sharpened all the pencils, the angle of the pencil tips become ( 7 − m ) ∘ , 2 ( 7 − m ) ∘ = 3 ∘ ∴ m = 1 Hence, m + n = 1 2 1 .