It happens!!
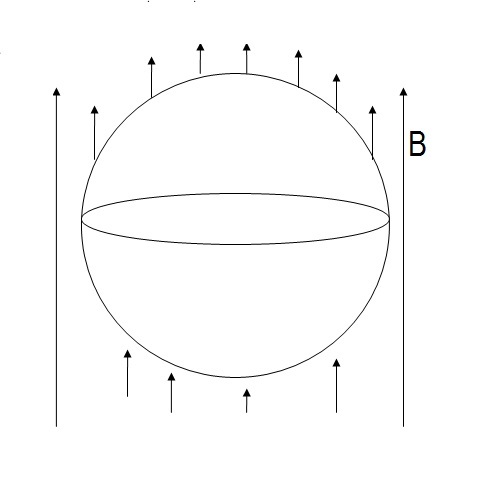
In the arrangement shown, a gas is filled inside a balloon, which is placed in a vertical magnetic field of intensity B . The initial volume of balloon is V o and the gas is filled inside it at the rate of a m 3 / s . If there is no leakage, the emf induced (in mV) at t = 8 π s e c , in a conducting ring which is elastic and placed horizontally along the circumference of balloon is n .
[Take B = 1 . 5 T , V o = ( 2 0 π ) m 3 , a = 2 ]
F i n d n
The answer is 606.7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Note that V = 3 4 π r 3 ⟹ π ( 4 π 3 ) 3 2 V 3 2 = π r 2 = A
Now, Φ = B A
And, ϵ = − ∂ t ∂ Φ = − B ∂ t ∂ ( π ( 4 π 3 ) 3 2 V 3 2 )
Furthermore, we notice that V ( t ) = 2 0 π + a t
Plugging in the above, and doing the appropriate differentiation, we get:
ϵ = − 2 3 a t + 2 0 π 3 2 / 3 3 2 π a
The value of which is equal to − 3 2 / 3 3 2 at t = π / 8 and a = 2
d t d V V 3 4 π r 3 4 π r 2 d t d r d t d r ϵ r ϵ = a = a t + V 0 = a t + V 0 ...1 = a = 4 π r 2 a = B d t d A = 2 π r B d t d r = 2 π r B 4 π r 2 a = 2 r a B = ( 1 6 2 4 3 ) 3 1 (from 1) = 2 × ( 1 6 2 4 3 ) 3 1 2 × 1 . 5 = 0 . 6 0 5 V