It Is All Circles
The problem below is a problem I saw on brillant which I slightly modified.
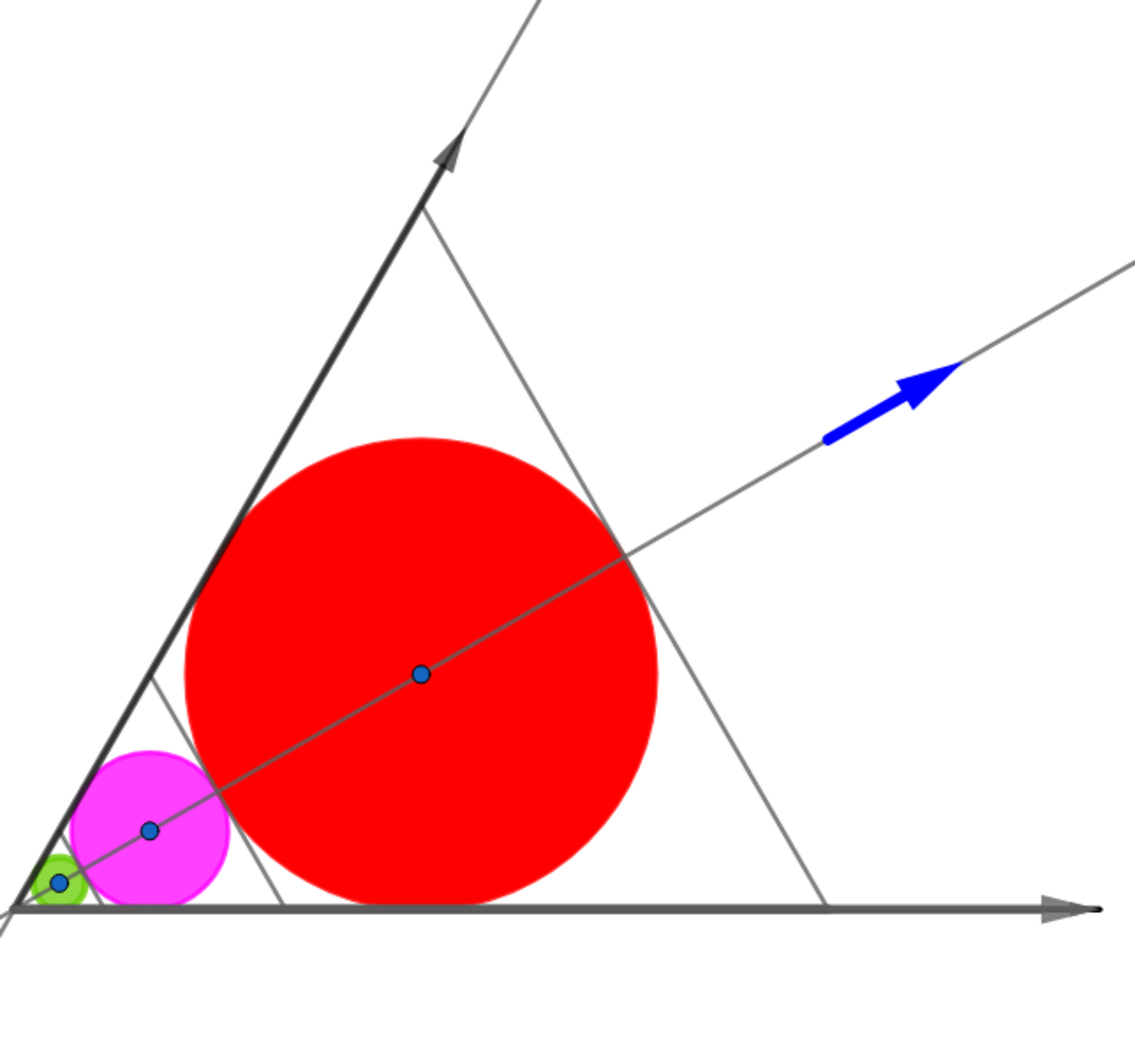
The two rays in the diagram make an angle of The first circle is tangent to both rays and has radius 1. Each successive circle is tangent to the two rays and externally tangent to the previous circle.
If the white region of the area in the diagram above for circles can be expressed as , where and are coprime positive integers, find .
The answer is 3912.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
For the first equilateral triangle with inscribed circle whose radius r 1 = 1 we have 2 3 1 x 1 = 1 ⟹ x 1 = 2 3 .
Using the tangents to the second circle the midpoint of the second equilateral triangle is 3 3 ⟹ the side of the second equilateral triangle is x 2 = 6 3 ⟹ r 2 = 3 . The two triangles are in proportion as is the two circles with common ratio 3 .
Using the tangents to the third circle the midpoint of the second equilateral triangle is 9 3 ⟹ the side of the second equilateral triangle is x 3 = 1 8 3 ⟹ r 3 = 3 .
In general the midpoint of the n th equilateral triangle is 3 n − 1 3 ⟹ the side of the n th equilateral triangle is x n = 2 3 ∗ 3 n − 1 ⟹ r n = 3 n − 1 ⟹
The area of the n th triangle with height h n = 2 3 ( 2 3 ∗ 3 n − 1 ) is A n ∗ = 3 2 n − 1 3 and the sum of the areas of the n circles is A n ∗ ∗ = π ∑ j = 1 n r j 2 = π ∑ j = 1 n 9 j − 1 = 8 ( 3 2 n − 1 ) π
⟹ The desired area A n = 3 2 n − 1 ( 3 − 8 3 π ) + 8 π = 8 3 2 n − 1 ( 8 3 − 3 π ) + 8 π .
For n = 1 9 5 4 ⟹ A = 2 3 3 3 9 0 7 ( 2 3 3 − 3 π ) + 2 3 π = c a a b ( c a a − a ) + c a π ⟹ a + b + c = 3 9 1 2 .