It is not a Beach Ball
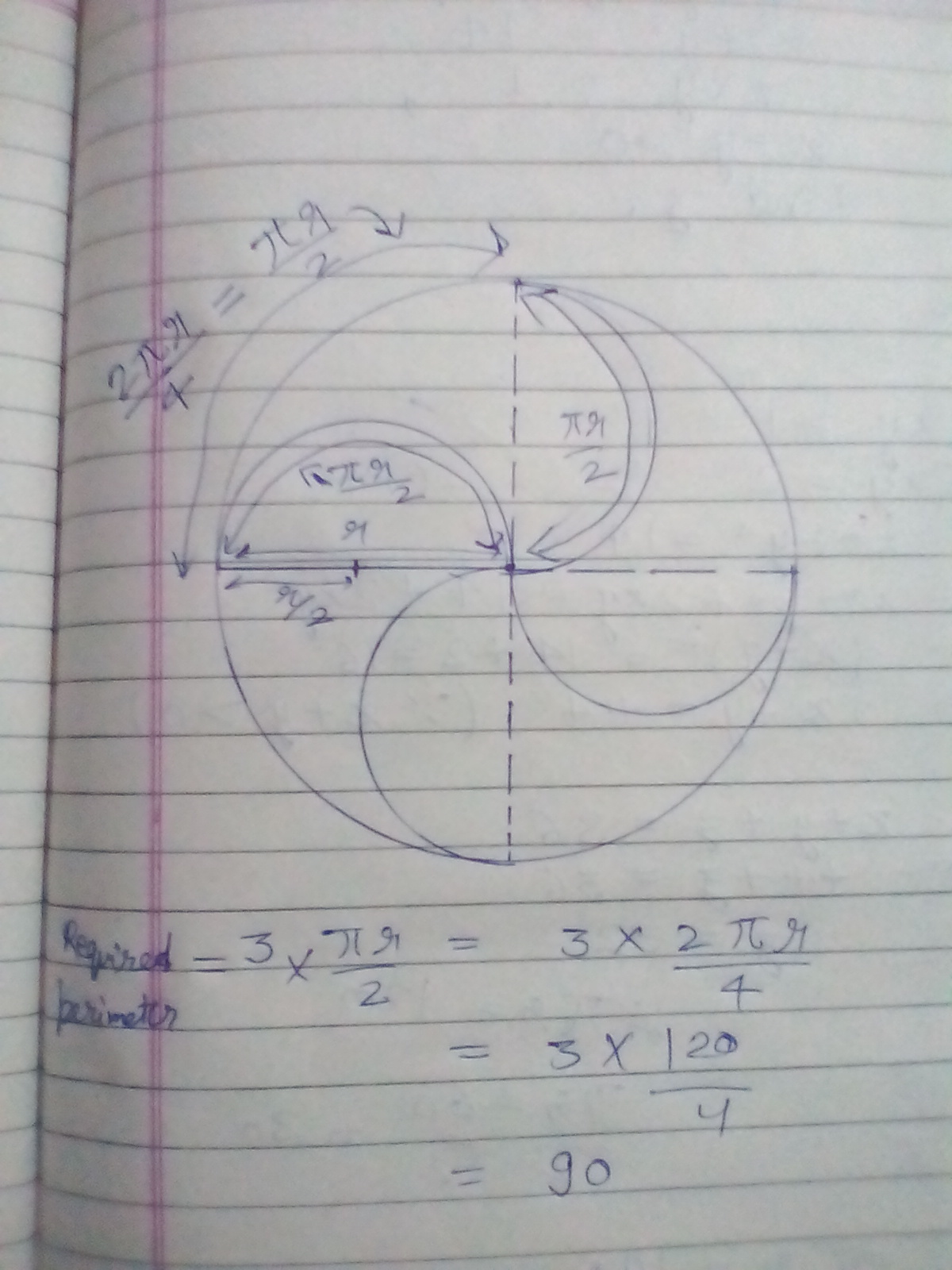
A circle is divided into four identical regions constructed out of overlapping quarter-circles and semicircles.
If the circumference of the circle is 120, then what is the perimeter of each region?
The construction of each region is shown here.
The answer is 90.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
Personally, I found b by quartering the circumference, and didn't bother with finding d, using c=2 pi r as the formula instead :)
Why isn't "60" used twice, as it occurs in the perimeter of the circle twice... (as a)
nice one dude :) @Kim Starlinger he is using it twice notice the "2a" ;)
Since the diameter is the half, the circumference of one small circle is half the circumference of the big circle.
The length of the circumference of the 2 small circles is equal the length of 1 big circle. They are borders to two areas, left and right hand side. So the length of all border lines together are 3 big circumferences (3x120)
Each of the 4 regions has a border length of 3/4 times 120 which is 90.
No pi needed.
Each region is bordered by one quarter of the large circle and two semicircles that have half the radius the large circle. Since the large circle has a circumference of 1 2 0 , the quarter curve has a length of 4 1 1 2 0 = 3 0 and the two semicircle curves have a length of 2 1 1 2 0 = 6 0 , and 3 0 + 6 0 = 9 0 .
Its not so obvious to me that half of circumference of circle with R will be equal to circumference of circle with R/2.😅
Log in to reply
C = 2 π R is the circumference formula.
We can divide both side by 2 and arrange to get:
2 C = 2 π 2 R
The problem was made much simpler.
This made it much simpler to understand
If you reduce the equations from Brilliant member, you can see the circumference parts work as shown by David, and it’s handy to know this shortcut :)
Notice in each region, there are two circumferences of semi circles and one circumference of a quarter of a circle.
The perimeter or circumference of a quarter of the large circle is = 4 1 2 0 = 3 0 .
The radius of the large circle is 2 π 1 2 0 .
The radius of one small semi circle is half the radius of the large circle: 4 π 1 2 0 .
⟹ the circumference of one semi-circle is 2 π 6 0 π = 3 0 ⟹ total perimeter is: 3 0 + 3 0 + 3 0 = 9 0
I thought question a little unclear- I had calculated the perimeter including the hidden portion of each region - 79.
Log in to reply
I think you did a terrible mistake because the perimeter is everything from the outside but l did this mistake so many times before, don’t worry.
the radius is actually 19.0985 2hich would make the total 30 (quarter of circumference) + 2 * Radius (38.19718834) so your answer is wrong, if the radius is 30 the circle would be much bigger (188.5)
120/4 = long part = 30
Each small circle is 1/2 (because the radios is the half) of the big one, so is the perimeter too. 120/2 is the perimeter of the small circle = 60. So, two halves = 2*(60/2) = 60.
30+60=90
The radius of the big circle is 60/pi
The edges of the blue region are made of:
One quarter of the circumference of the big circle = 30
And (in two parts) circumference of a circle with radius 30/pi
This gives a total of 90
Thank you for sharing your solution.
The circumference of the large circle is 120. The circumference of the smaller circle, with half the diameter, would be 1/2 of that, or 60. And the half-circumference of that smaller circle would be 30, which would be the length of each of the "heads" of the swirls. And the outer arc is just 1/4th of the circumference of the big circle, which is another 30 units. So, 30+30+30=90 as the perimeter of the swirl ☺☺☺☺
The small half-circles can be rearranged to form two full circles, each having half the diameter of the large circle. The total of all perimeters is therefore the large circle, plus TWICE the total circumference of the two small circles, as the small circles, being part of the perimeter of TWO neighboring shapes everywhere, need to be counted twice. (The large circle only counts once, as it is not on a shared boundary.)
The small circles have half the circumference of the large circle, as their diameter is half as large. So 120 + 2 x 2 x (120/2) = 360. Divide by four, as there are four identical shapes, and you get the answer: 360/4 = 90. (No Pi() required!!!)
A quarter circle is .25 x 120 = 30 The semi-circle is equivalent to 1/4 of the large circle and therefore also .25 x 120 = 30 You have one quarter circle and two semi-circles in each color region, so .75 x 120 = 90
The circumference of a circle is given by c = π d , where d is the diameter. Substituting, we have
1 2 0 = π d
d = π 1 2 0
It follows that the radius is r = π 6 0
The diameter of each blue semicircular arc a is π 6 0 . So
2 a = 2 ( 2 1 ) ( π ) ( π 6 0 ) = 6 0
It follows that the length of b is
b = 4 1 ( π ) ( π 1 2 0 ) = 3 0
So the required perimeter is
P = 2 a + b = 6 0 + 3 0 = 9 0