It is simple if you think about it

Geometry Level 3

If a line is drawn through a fixed point P ( α , β ) P(\alpha,\beta) to the circle x 2 + y 2 = a 2 x^2 + y^2 = a^2 at A A and B B , then express P A × P B PA \times PB in terms of α , β \alpha,\beta and/or α \alpha .

α 2 + β 2 − a 2 \alpha^2 + \beta^2 - a^2 a 2 a^2 α 2 + β 2 + a 2 \alpha^2 + \beta^2 + a^2 α 2 + β 2 \alpha^2 + \beta^2

View wiki
Vishwak Srinivasan by Vishwak Srinivasan , 24, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

From the image above and using Tangent-Secant theorem, it is known that

P A × P B = P T 2 PA \times PB = PT^2

Using notation as found in S.L.Loney's Coordinate geometry (to avoid ambiguity):

The length of the tangent, i.e., P T = S 1 PT = \sqrt{S_1}

S 1 = α 2 + β 2 − a 2 \sqrt{S_1} = \sqrt{\alpha^2 + \beta^2 - a^2}

P A × P B = P T 2 = S 1 = α 2 + β 2 − a 2 PA \times PB = PT^2 = S_1 = \boxed{\alpha^2 + \beta^2 - a^2}

Note

  • S 1 S_1 is nothing but a point substituted in the circle S = 0 S = 0 , i.e., x 2 + y 2 − a 2 = 0 x^2 + y^2 - a^2 = 0
4 Helpful 0 Interesting 0 Brilliant 0 Confused

If one was pressed for time, maybe one could assume ( α , β ) (\alpha, \beta) to be a point on the circle. Then, α 2 + β 2 = a 2 ⋅ \displaystyle \alpha^{2} + \beta^{2} = a^{2} \cdot

Moreover, P A × P B = 0 \displaystyle PA \times PB = 0 and the result follows from the options.

Nice Solution by the way ! Cheers

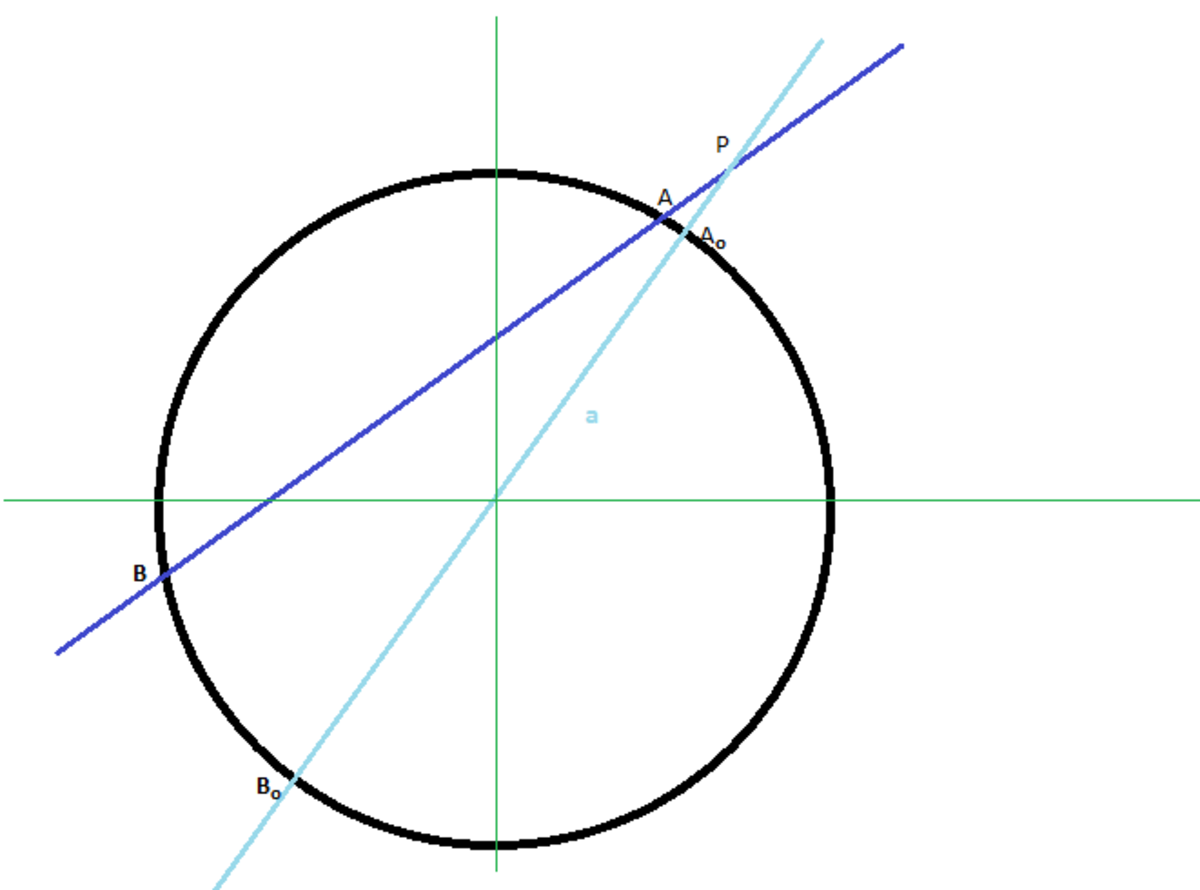
B.S.Bharath Sai Guhan - 5 years, 3 months ago

Draw a diameter A 0 B 0 A_0 B_0 passing through P.

P A ∗ P B = P A 0 ∗ P B 0 PA*PB=PA_0*PB_0

from the diagram we can see that P A 0 = r − a PA_0=r-a & P B 0 = r + a PB_0=r+a where r = α 2 + β 2 r=\sqrt{\alpha^2+\beta^2}

So our equation now becomes

P A ∗ P B = ( r − a ) ( r + a ) = r 2 − a 2 = α 2 + β 2 − a 2 PA*PB=(r-a)(r+a)=r^2-a^2=\alpha^2+\beta^2-a^2

2 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...