It Looks Like A Pause Button

Geometry Level 2

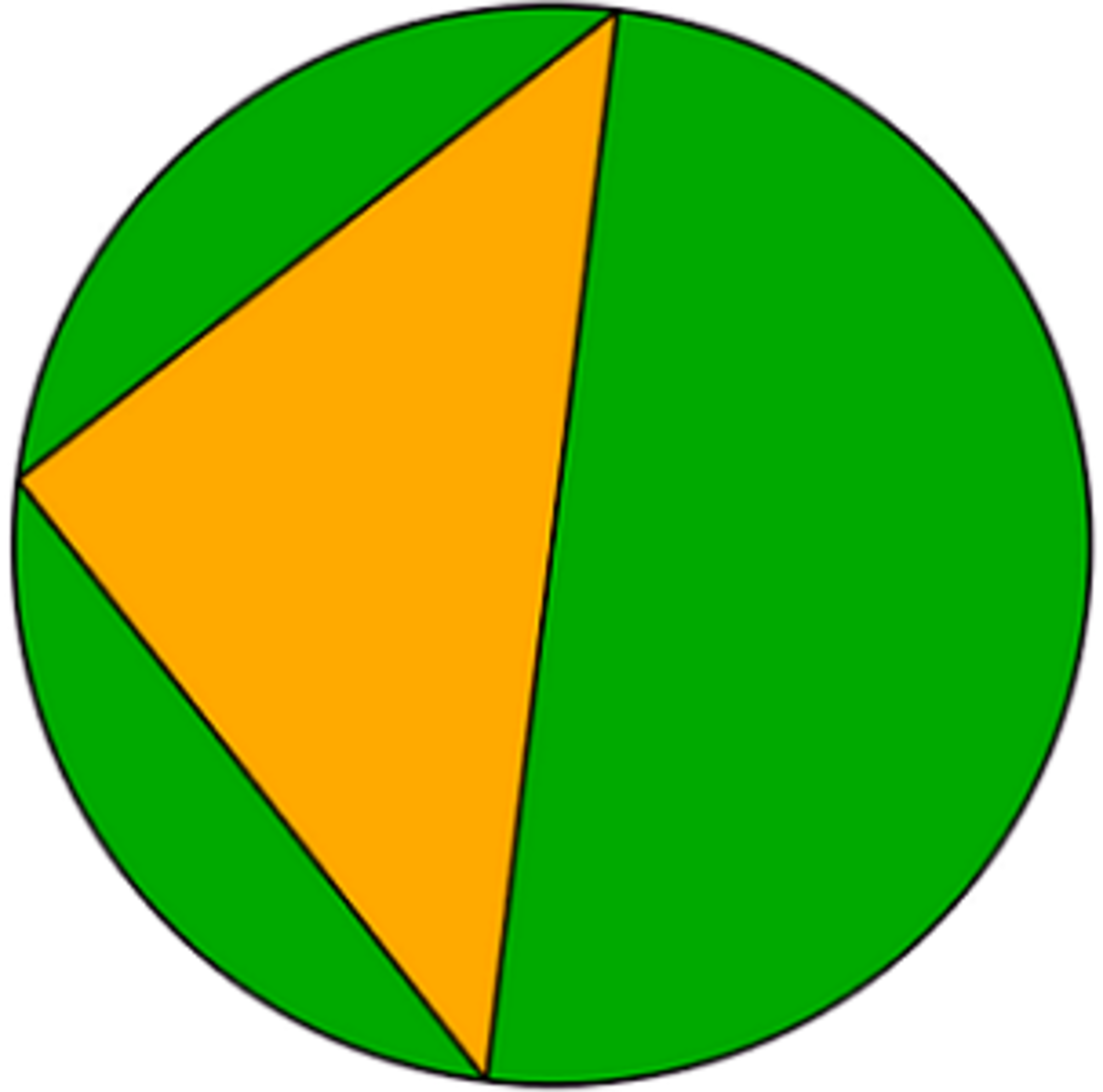
The figure above shows a right triangle inscribed in a circle of diameter 58. If each side lengths of the triangle is an integer, then what is the area of the green region?

841\pi - 920

841\pi - 800

841\pi - 880

841\pi - 840

1 solution

Namit Jain
Apr 29, 2016

Since this is a right angled triangle with all the points touching the circle, by Thales' theorem we know that the diameter is the hypotenuse of the triangle. Since it's mentioned that both the numbers are integers, using Pythagorus theorem we can figure out both the sides

$a^{2}+b^{2}=58^{2}$ which is 3364

now we need 2 integers whose squares sum up to 3364

Dividing 3364 by 2 gives 1682 (since there are 2 sides)

$\sqrt{1682}$ ~ 41, that tells us both the integers are close to 41, they are 40 & 42

The sides of the triangle are 40-42-58 and the area of the triangle is 840

Hence the answer is 841 π - 840

Note to the publisher : It looks like a play button not pause :p

Moderator note:

The claim that "that tells us both the integers are close to 41" is not necessarily true. For example, the 5-12-13 right triangle doesn't have 2 legs that are close to $\sqrt{ 85} \approx 9$ .

Instead, to solve $a^2 + b^2 = n^2$ , we either use trial and error, or consider the Gaussian factorization of $n^2$ .

Great Thanks! Yes, for some unknown reason, my old VCD player has a "pause" button like that.

Chung Kevin - 5 years, 1 month ago

It Looks Like A Pause Button

1 solution

Moderator note:

0 pending reports