It looks symmetric...

Geometry Level 1

If cos ⁡ 4 α cos ⁡ 2 β + sin ⁡ 4 α sin ⁡ 2 β = 1 , \quad \quad \dfrac{\cos^4\alpha}{\cos^2\beta}+\dfrac{\sin^4\alpha}{\sin^2\beta}=1, find the value of sin ⁡ 4 β sin ⁡ 2 α + cos ⁡ 4 β cos ⁡ 2 α . \dfrac{\sin^4\beta}{\sin^2\alpha}+\dfrac{\cos^4\beta}{\cos^2\alpha}.


The answer is 1.

View wiki
Sandeep Bhardwaj by Sandeep Bhardwaj , 28, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

4 solutions

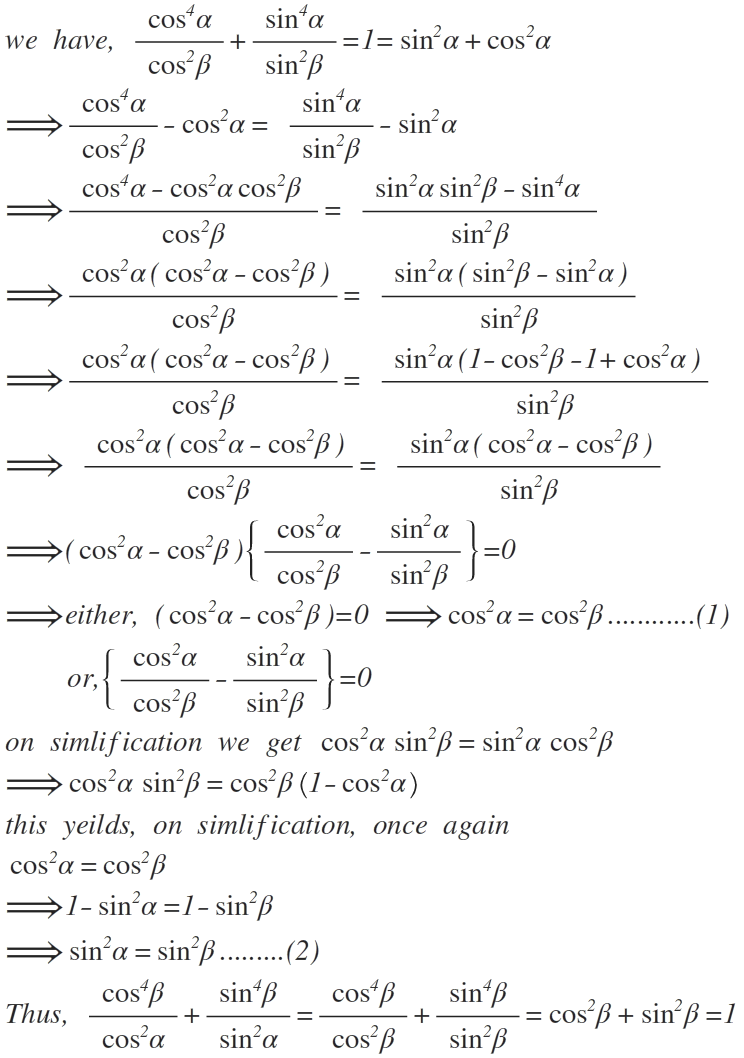
13 Helpful 1 Interesting 1 Brilliant 1 Confused

Nice solution!!!! i think on the RHS of the 2nd line, the 2 terms should be switched right???

Willia Chang - 4 years, 11 months ago
U Z
Nov 10, 2014

let α = a , β = b \alpha =a , \beta = b

c o s 4 a c o s 2 a + s i n 4 a s i n 2 a = 1 \frac{cos^{4}a}{cos^{2}a} + \frac{sin^{4}a}{sin^{2}a} = 1

We observe that for R.H.S to be one , the possibilities are

  • a = 0 , b < π 2 a = 0 , b < \frac{\pi}{2}

  • If no term on L.H.S is 0 , then c o s 2 b > c o s 4 a cos^{2}b > cos^{4}a , s i n 2 b > s i n 4 a sin^{2}b > sin^{4}a

For first , since b is not 0 , then L.H.S would always be greater than 1 .Thus a=0 is not possible.

For 2 we see 2 conditions at the same time , b<a(cos is decreasing function) , a<b(sine is increasing function) , thus it shows that the solution is the vertex of the curve that is a=b

Hence answer is 1.

11 Helpful 0 Interesting 1 Brilliant 0 Confused

While it is true that sin^2 a + cos^2 a = 1 for all a. in the second line a <> 0 because division by 0 (sin^2 0 = 0) is prohibited.

Tom Capizzi - 4 years, 9 months ago
Sanjeet Raria
Nov 9, 2014

Note: My solution is unconventional.

Simply by observing, it turns out that if cos ⁡ 2 α = cos ⁡ 2 β ( ⇒ sin ⁡ 2 α = sin ⁡ 2 β ) , \cos^2 \alpha= \cos^2 \beta (\Rightarrow \sin^2 \alpha= \sin^2 \beta) , the given equation is satisfied.

That means putting cos ⁡ 2 α = cos ⁡ 2 β ( ⇒ sin ⁡ 2 α = sin ⁡ 2 β ) \cos^2 \alpha= \cos^2 \beta (\Rightarrow \sin^2 \alpha= \sin^2 \beta) will give the value of required expression which comes out to be sin ⁡ 2 β + cos ⁡ 2 β = 1 \sin^2 \beta +\cos^2 \beta=\boxed 1

5 Helpful 0 Interesting 1 Brilliant 0 Confused

Good observation, Sanjeet!

You don't always need the most theoretical approach for solving everything (Though, one should know that).

Such observations make complicated questions quite easy and are needed for objective exams prep.

I appreciate the way you did that (Of course, I clearly state that I don't criticize the theoretical approach; please don't misunderstand my appreciation, 'cause when no observation strikes your mind,you need to rely on theoretical method.)

Ninad Akolekar - 6 years, 7 months ago

Or simply observed that α = β = 4 5 ∘ \alpha = \beta = 45^\circ satisfy the equation. Sometimes, solving a problem by simply plugging in a value is way faster, good job!

Christopher Boo - 6 years, 7 months ago

Note that cos ⁡ 2 α = cos ⁡ 2 β \cos^2 \alpha= \cos^2 \beta is the necessary & sufficient condition for the first equation, one can prove it, though the proof is long.

For the general values, you can observe that for a given α \alpha the value of β \beta is given by the equation β = n π ± α \beta =nπ \pm \alpha @Christopher Boo @Ninad Akolekar

Sanjeet Raria - 6 years, 7 months ago

Let us prove that the condition cos ⁡ 4 α cos ⁡ 2 β + sin ⁡ 4 α sin ⁡ 2 β = 1 ( ∗ ) \frac{\cos^4\alpha}{\cos^2 \beta}+\frac{\sin^4\alpha}{\sin^2 \beta}=1\quad\quad (*) is equivalent to cos ⁡ 2 α = cos ⁡ 2 β \cos^2 \alpha =\cos^2\beta and sin ⁡ 2 α = sin ⁡ 2 β \sin^2\alpha=\sin^2\beta .

We can use the fact that for any pair of numbers ( x , y ) (x, y) satisfy that x 2 + y 2 = 1 , x^2+y^2=1, if and only if, there is an angle θ , \theta, such that x = cos ⁡ θ x=\cos\theta and y = sin ⁡ θ . y=\sin\theta. If we apply this property to the pair ( cos ⁡ 2 α cos ⁡ β , sin ⁡ 2 α sin ⁡ β ) , (\frac{\cos^2\alpha}{\cos \beta},\frac{\sin^2\alpha}{\sin \beta}), then the condition ( ∗ ) (*) for the angles α \alpha and β \beta is true if and only if there is an angle θ \theta such that cos ⁡ 2 α cos ⁡ β = cos ⁡ θ ( ∗ ∗ ) \frac{\cos^2\alpha}{\cos \beta}=\cos\theta \quad\quad (**) and sin ⁡ 2 α sin ⁡ β = sin ⁡ θ ( ∗ ∗ ∗ ) . \frac{\sin^2\alpha}{\sin \beta}=\sin\theta\quad\quad(***).

Solving the last two equations for cos ⁡ 2 α \cos^2 \alpha and sin ⁡ 2 α , \sin^2\alpha, respectively, and adding the resulting equations, we get that cos ⁡ β cos ⁡ θ + sin ⁡ β sin ⁡ θ = 1. \cos\beta\cos\theta+\sin\beta\sin\theta=1. That is, cos ⁡ ( β − θ ) = 1 \cos (\beta-\theta)=1 and, therefore, β = θ + 2 n π \beta=\theta+ 2n\pi where n n is any integer. Hence cos ⁡ β = cos ⁡ θ \cos \beta=\cos\theta and sin ⁡ β = sin ⁡ θ . \sin \beta= \sin\theta. Now the equations ( ∗ ∗ ) (**) and ( ∗ ∗ ∗ ) (***) can be rewritten in the form cos ⁡ 2 α cos ⁡ β = cos ⁡ β \frac{\cos^2\alpha}{\cos \beta}=\cos\beta and sin ⁡ 2 α sin ⁡ β = sin ⁡ β . \frac{\sin^2\alpha}{\sin \beta}=\sin\beta. From this, we get that the condition ( ∗ ) (*) is equivalent to cos ⁡ 2 α = cos ⁡ 2 β \cos^2 \alpha =\cos^2\beta and sin ⁡ 2 α = sin ⁡ 2 β . \sin^2\alpha=\sin^2\beta.

Arturo Presa - 4 years, 1 month ago
Arturo Presa
May 14, 2017

The solution that I will present here is similar to the one of @Sanjeet Raria , but including some necessary details. First, let us prove that the condition cos ⁡ 4 α cos ⁡ 2 β + sin ⁡ 4 α sin ⁡ 2 β = 1 ( ∗ ) \frac{\cos^4\alpha}{\cos^2 \beta}+\frac{\sin^4\alpha}{\sin^2 \beta}=1\quad\quad (*) is equivalent to cos ⁡ 2 α = cos ⁡ 2 β \cos^2 \alpha =\cos^2\beta and sin ⁡ 2 α = sin ⁡ 2 β \sin^2\alpha=\sin^2\beta .

We can use the fact that any pair of numbers ( x , y ) (x, y) satisfies that x 2 + y 2 = 1 , x^2+y^2=1, if and only if there is an angle θ , \theta, such that x = cos ⁡ θ x=\cos\theta and y = sin ⁡ θ . y=\sin\theta. If we apply this property to the pair ( cos ⁡ 2 α cos ⁡ β , sin ⁡ 2 α sin ⁡ β ) , (\frac{\cos^2\alpha}{\cos \beta},\frac{\sin^2\alpha}{\sin \beta}), then the condition ( ∗ ) (*) for the angles α \alpha and β \beta is true if and only if there is an angle θ \theta such that cos ⁡ 2 α cos ⁡ β = cos ⁡ θ ( ∗ ∗ ) \frac{\cos^2\alpha}{\cos \beta}=\cos\theta \quad\quad (**) and sin ⁡ 2 α sin ⁡ β = sin ⁡ θ ( ∗ ∗ ∗ ) . \frac{\sin^2\alpha}{\sin \beta}=\sin\theta\quad\quad(***).

Solving the last two equations for cos ⁡ 2 α \cos^2 \alpha and sin ⁡ 2 α , \sin^2\alpha, respectively, and adding the resulting equations, we get that cos ⁡ β cos ⁡ θ + sin ⁡ β sin ⁡ θ = 1. \cos\beta\cos\theta+\sin\beta\sin\theta=1. That is, cos ⁡ ( β − θ ) = 1 \cos (\beta-\theta)=1 and, therefore, β = θ + 2 n π \beta=\theta+ 2n\pi where n n is any integer. Hence cos ⁡ β = cos ⁡ θ \cos \beta=\cos\theta and sin ⁡ β = sin ⁡ θ . \sin \beta= \sin\theta. Now the equations ( ∗ ∗ ) (**) and ( ∗ ∗ ∗ ) (***) can be rewritten in the form cos ⁡ 2 α cos ⁡ β = cos ⁡ β \frac{\cos^2\alpha}{\cos \beta}=\cos\beta and sin ⁡ 2 α sin ⁡ β = sin ⁡ β . \frac{\sin^2\alpha}{\sin \beta}=\sin\beta. From this, we get that the condition ( ∗ ) (*) is equivalent to cos ⁡ 2 α = cos ⁡ 2 β \cos^2 \alpha =\cos^2\beta and sin ⁡ 2 α = sin ⁡ 2 β . \sin^2\alpha=\sin^2\beta.
Once, we have proved this, it easy to see that the expression sin ⁡ 4 β sin ⁡ 2 α + cos ⁡ 4 β cos ⁡ 2 α = sin ⁡ 2 α + cos ⁡ 2 α = 1. \dfrac{\sin^4\beta}{\sin^2\alpha}+\dfrac{\cos^4\beta}{\cos^2\alpha}= \sin^2 \alpha+\cos^2\alpha=1.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...