It should be in Combinatorics section
If the series above is true for constants , find the value of .
This question is part of set Serieses are fun! .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
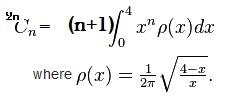
Just showing what Abhishek Sharma meant.
r = 1 ∑ ∞ 2 2 r ( 2 r + 1 ) 2 r C r = 4 ˙ 3 2 + 1 6 ˙ 5 6 + 6 4 ˙ 7 2 0 + 2 5 6 ˙ 9 7 0 + . . . = 6 1 + 4 0 3 + 1 1 2 5 + 1 1 5 2 3 5 + . . . As sin − 1 x = x + 6 1 x 3 + 4 0 3 x 5 + 1 1 2 5 x 7 + 1 1 5 2 3 5 x 9 + . . . = sin − 1 ( 1 ) − 1 = 2 π − 1
⇒ a + b = 2 + 1 = 3