It Shouldn't be this Hard
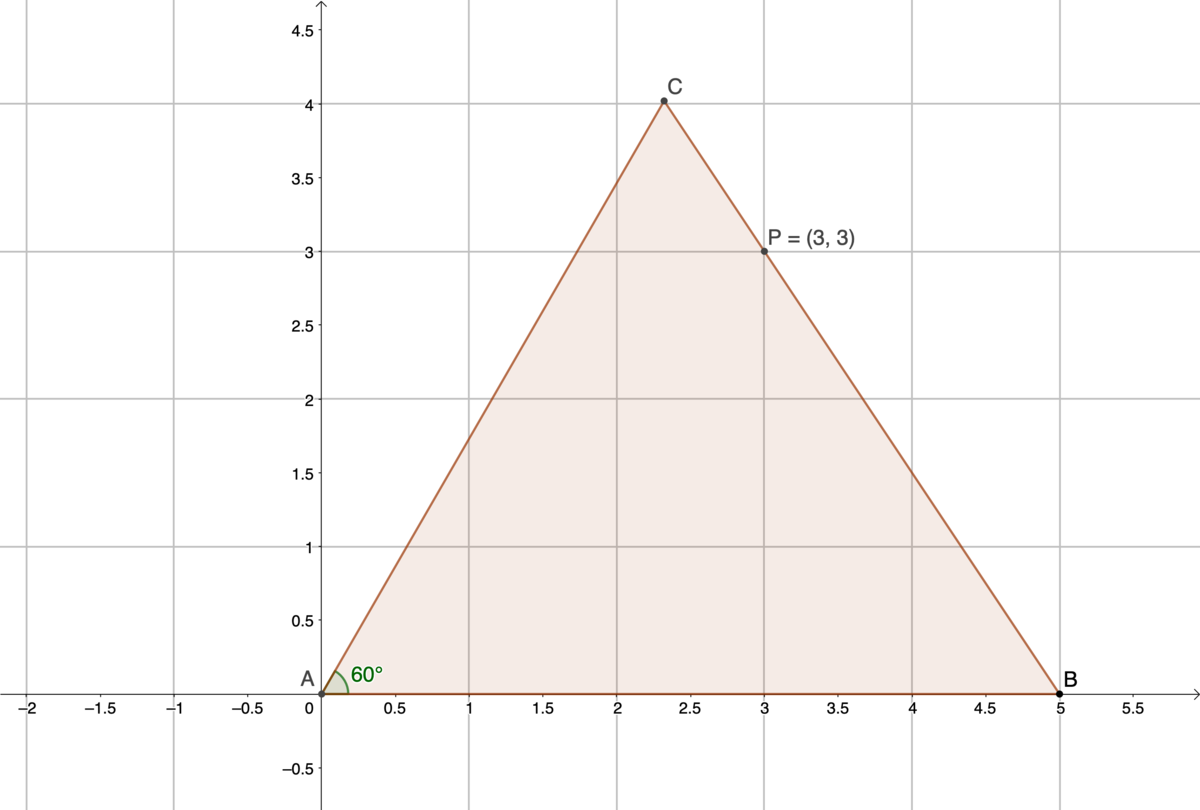
In △ A B C , ∠ C A B = 6 0 ∘ , A = ( 0 , 0 ) . Side B C passes through point P = ( 3 , 3 ) . Given these constraints, what is the shortest length of B C ? Submit ⌊ 1 0 5 ⋅ B C ⌋
The answer is 462585.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Holy smokes, you are fast! It took me several days. Nice work, Pi Han.
Let ∠ B = θ . By sine rule, A P C P = sin ∠ A C P sin ∠ C A P = sin ( 1 2 0 ∘ − θ ) sin 1 5 ∘ = sin ( 6 0 ∘ + θ ) sin 1 5 ∘ . And A D B P = sin ∠ P B A sin ∠ P A B = sin θ sin 4 5 ∘ . ⟹ B P C P = sin 4 5 ∘ sin ( 6 0 ∘ + θ ) sin 1 5 ∘ sin θ .
Let B C = a . Then B P C P = 3 a sin θ − 3 = sin 4 5 ∘ sin ( 6 0 ∘ + θ ) sin 1 5 ∘ sin θ and:
a d θ d a = sin 4 5 ∘ sin θ sin ( 6 0 ∘ + θ ) 3 sin 1 5 ∘ sin θ + 3 sin 4 5 ∘ sin ( 6 0 ∘ + θ ) = sin 4 5 ∘ ( cos 6 0 ∘ − cos ( 2 θ + 6 0 ∘ ) ) 3 ( cos ( θ − 1 5 ∘ ) − cos ( θ + 1 0 5 ∘ ) ) = sin 4 5 ∘ ( cos 6 0 ∘ − cos ( 2 θ + 6 0 ∘ ) ) 3 sin 6 0 ∘ sin ( θ + 4 5 ∘ ) = 1 − 2 cos ( 2 θ + 6 0 ∘ ) 6 6 sin ( θ + 4 5 ∘ ) = ( 1 − 2 cos ( 2 θ + 6 0 ∘ ) ) 2 6 6 ( cos ( θ + 4 5 ∘ ) ( 1 − 2 cos ( 2 θ + 6 0 ∘ ) ) − 4 sin ( θ + 4 5 ∘ ) sin ( 2 θ + 6 0 ∘ ) )
As there is no maximum value of a , to find min ( a ) , we find the θ such that d θ d a = 0 .
cos ( θ + 4 5 ∘ ) ( 1 − 2 cos ( 2 θ + 6 0 ∘ ) ) 4 sin ( 2 θ + 6 0 ∘ ) 1 − 2 cos ( 2 θ + 6 0 ∘ ) 2 3 cos 2 θ + 2 sin 2 θ 1 − cos 2 θ + 3 sin 2 θ 2 3 − 2 3 t 2 + 4 t 1 + t 2 − 1 + t 2 + 2 3 t 3 + 2 t − 3 t 2 3 t + t 2 ( 3 − 1 ) t 3 − t 2 − 2 t − 3 = 4 sin ( θ + 4 5 ∘ ) sin ( 2 θ + 6 0 ∘ ) = tan ( θ + 4 5 ∘ ) = 1 − tan θ 1 + tan θ = 1 − t 1 + t = 1 − t 1 + t = 0 Let t = tan θ
Solving the cubic equation, we have t ≈ 2 . 7 0 1 5 1 9 5 6 5 and min ( a ) = 3 t + t 2 3 2 ( 1 + t ) 1 + t 2 ≈ 4 . 6 2 5 8 5 8 7 2 5 . Therefore ⌊ 1 0 5 min ( a ) ⌋ = 4 6 2 5 8 5 .
Draw A P , which by the distance formula a length of A P = ( 3 − 0 ) 2 + ( 3 − 0 ) 2 = 3 2 .
Since by the slopes formula tan ∠ P A B = 3 − 0 3 − 0 , ∠ A P B = 4 5 ° , this makes ∠ P A C = ∠ C A B − ∠ P A B = 6 0 ° − 4 5 ° = 1 5 ° .
Let θ = ∠ A P B . Then from the straight line ∠ A P C = 1 8 0 ° − θ and by the angle sums of △ A P C and △ A P B , ∠ P B A = 1 3 5 ° − θ and ∠ P C A = θ − 1 5 ° .
By the law of sines on △ A P C , C P = sin ( θ − 1 5 ° ) 3 2 sin 1 5 ° , and by the law of sines on △ A P B , P B = sin ( 1 3 5 ° − θ ) 3 2 sin 4 5 ° , so B C = sin ( θ − 1 5 ° ) 3 2 sin 1 5 ° + sin ( 1 3 5 ° − θ ) 3 2 sin 4 5 ° .
The minimum will occur when d θ d B C = − sin 2 ( θ − 1 5 ° ) 3 2 sin 1 5 ° cos ( θ − 1 5 ° ) + sin 2 ( 1 3 5 ° − θ ) 3 2 sin 4 5 ° cos ( 1 3 5 ° − θ ) = 0 , which solves numerically to θ ≈ 6 5 . 3 1 2 6 3 9 6 5 6 2 ° .
Substituting θ value into the equation for B C gives B C ≈ 4 . 6 2 5 8 5 8 7 2 5 , so ⌊ 1 0 5 ⋅ B C ⌋ = 4 6 2 5 8 5 .
Let the x -coordinate of B be n > 0 , and since the ratio of the y -coordinate and the x -coordinate of the coordinate C is tan ( 6 0 ∘ ) = 3 , we can denote the coordinate of C to be ( m , m 3 ) , where 0 < m ⩽ 3 .
Define D as the square of the distance B C , then using the distance formula , D = ( m 3 ) 2 + ( m − n ) 2 = 3 m 2 + ( m − n ) 2 .
Since P ( 3 , 3 ) passes through the straight line B C , the gradients of the straight line C P , P B , B C are all identical: m − 3 m 3 − 3 = 3 − n 3 = m − n m 3 .
Setting n as the subject gives n = m 3 − 3 3 m ( m 3 − 1 ) .
Thus, upon substitution, we can express D as a single variable function, D = ( m 3 − 3 ) 2 6 m 2 ( 2 m 2 − 3 ( 1 + 3 ) m + 9 ) .
At the critical point, d m d D = 0 ⟹ m ⋅ 3 3 m 3 − 2 7 m 2 + 2 7 3 m − 2 7 ( 2 4 3 ) m 3 + m 2 ( − 1 9 8 − 1 8 3 ) + m ( 1 6 2 + 1 6 2 3 ) − 3 2 4 = 0
Simplifying this gives m 3 ( 4 3 ) + m 2 ( − 3 3 − 3 3 ) + m ( 2 7 + 2 7 3 ) − 5 4 = 0 . Using Cardano's method , we get m = 4 3 1 1 + 3 + 6 2 7 6 4 8 q − 6 6 9 1 2 ⋅ q 7 3 − 8 ≈ 2 . 5 0 4 6 5 3 7 5 7 , where q = 3 3 9 1 − 1 9 5 3 + 2 5 8 8 7 6 − 1 4 7 7 4 4 3 .
Checking the endpoints of the domain 0 < m ⩽ 3 , the critical point of D ( 2 . 5 0 4 6 5 3 7 5 7 ) is smaller than D ( 0 ) and D ( 3 ) . Hence, this critical point must be a minimum value.
We have min ( D ) ≈ 2 1 . 3 9 8 5 6 8 9 4 1 1 7 0 6 4 8 1 9 6 5 8 6 5 2 with coordinates B ≈ ( 4 . 1 1 0 4 8 6 1 2 7 6 , 0 ) , C ≈ ( 2 . 5 0 4 6 5 3 7 5 7 9 4 9 , 4 . 3 3 8 1 8 7 5 6 4 ) .
The answer is ⌊ 1 0 5 ⋅ 2 1 . 3 9 8 5 6 8 9 4 1 1 7 0 6 4 8 1 9 6 5 8 6 5 2 3 … ⌋ = 4 6 2 5 8 5 .
Addendum:
Even if we allow n < 0 , that is, the x -coordinate of B is negative, then the straight line B C can never pass through ( 3 , 3 ) . A simple graphing shows that the straight A C and B C does not intersect at the coordinate C .
The maximum value of the length B C is 3 3 , and it occurs when A B C is a right triangle at ∠ B , with m = n = 3 .