It was delicious

The tip is given by

$\large \sqrt[3] {\large i^2\large e^{i\pi}+\left(\dfrac{4!}{\pi}\displaystyle \sum_{n=0}^{\infty} \dfrac{(-1)^n}{2n+1}\right)+\left(\dfrac{3!}{\pi^2}\displaystyle \sum_{n=1}^{\infty} \dfrac{1}{n^2}\right)}+\dfrac{4!}{3!}$

$\large i^2\large e^{i\pi}=-1\times i^2=1$

Consider,

$\displaystyle \sum_{n=0}^{\infty} \dfrac{(-1)^n}{2n+1}$

We know that , $\tan^{-1}x=x-\dfrac{x^3}{3}+\dfrac{x^5}{5}\dots$ ,assigning $x=1$ ,we get the reqired sum $=\tan^{-1}1=\dfrac{\pi}{4}$

also we have ,

$\displaystyle \sum_{n=1}^{\infty} \dfrac{1}{n^2}=\zeta(2)=\dfrac{\pi^2}{6}$

plugging these values back into the equation we get

$TIP=\large \sqrt[3] {1+\left(\dfrac{4!}{\pi}\dfrac{\pi}{4}\right)+\left(\dfrac{3!}{\pi^2}\dfrac{\pi^2}{6}\right)}+\dfrac{4!}{3!}=\large \sqrt[3] {1+6+1}+4=6$

Thus cost of food= Total cost- Cost of tip = $33.82-6=\boxed{27.82}$

The tip given can be solved by following steps: $\begin{aligned} & Sum &=& \large \sqrt[3] {\large i^2\large e^{i\pi}+\left(\dfrac{4!}{\pi}\displaystyle \sum_{n=0}^{\infty} \dfrac{(-1)^n}{2n+1}\right)+\left(\dfrac{3!}{\pi^2}\displaystyle \sum_{n=1}^{\infty} \dfrac{1}{n^2}\right)}+\dfrac{4!}{3!} \\ & &=& \large \sqrt[3] {\large 1+\left(\dfrac{4!}{\pi}\displaystyle \sum_{n=0}^{\infty} \dfrac{(-1)^n}{2n+1}\right)+\left(\dfrac{3!}{\pi^2}\displaystyle \sum_{n=1}^{\infty} \dfrac{1}{n^2}\right)}+4 & & \small \color{#3D99F6} {\text{Using Euler's identity } e^{i \pi}+1=0 \text{ we get } i^2e^{i \pi}=1 } \\ & &=& \large \sqrt[3] {\large 1+\left(\dfrac{4!}{\pi}\displaystyle \sum_{n=0}^{\infty} \dfrac{(-1)^n}{2n+1}\right)+\left(\dfrac{3!}{\pi^2}\dfrac{\pi^2}{6}\right)}+4 & & \small \color{#3D99F6} {\text{Basel's problem } \displaystyle \sum_{n=1}^{\infty} \dfrac{1}{n^2}=\dfrac{\pi^2}{6} } \\ & &=& \large \sqrt[3] {\large 1+\left(\dfrac{4!}{\pi}\dfrac{\pi}{4}\right)+\left(\dfrac{3!}{\pi^2}\dfrac{\pi^2}{6}\right)}+4 & & \small \color{#3D99F6} {\text{Assigning 1 in } tan^{-1} x=x- \dfrac{x^3}{3}+ \dfrac{x^5}{5}\dots \text{ we get }tan^{-1}1=\dfrac\pi4 } \\ & &=& \large \sqrt[3] {\large 1+6+1}+4 \\ & &=& 2+4 \\ & &=& \$ 6 \\ \end{aligned}$ So as the total bill was of $\$33.82$ including the tip and food charges,

$\begin{aligned} &Food &charges =33.82-6 \\ &Food &charges =\boxed{\$27.82} \\ \end{aligned}$

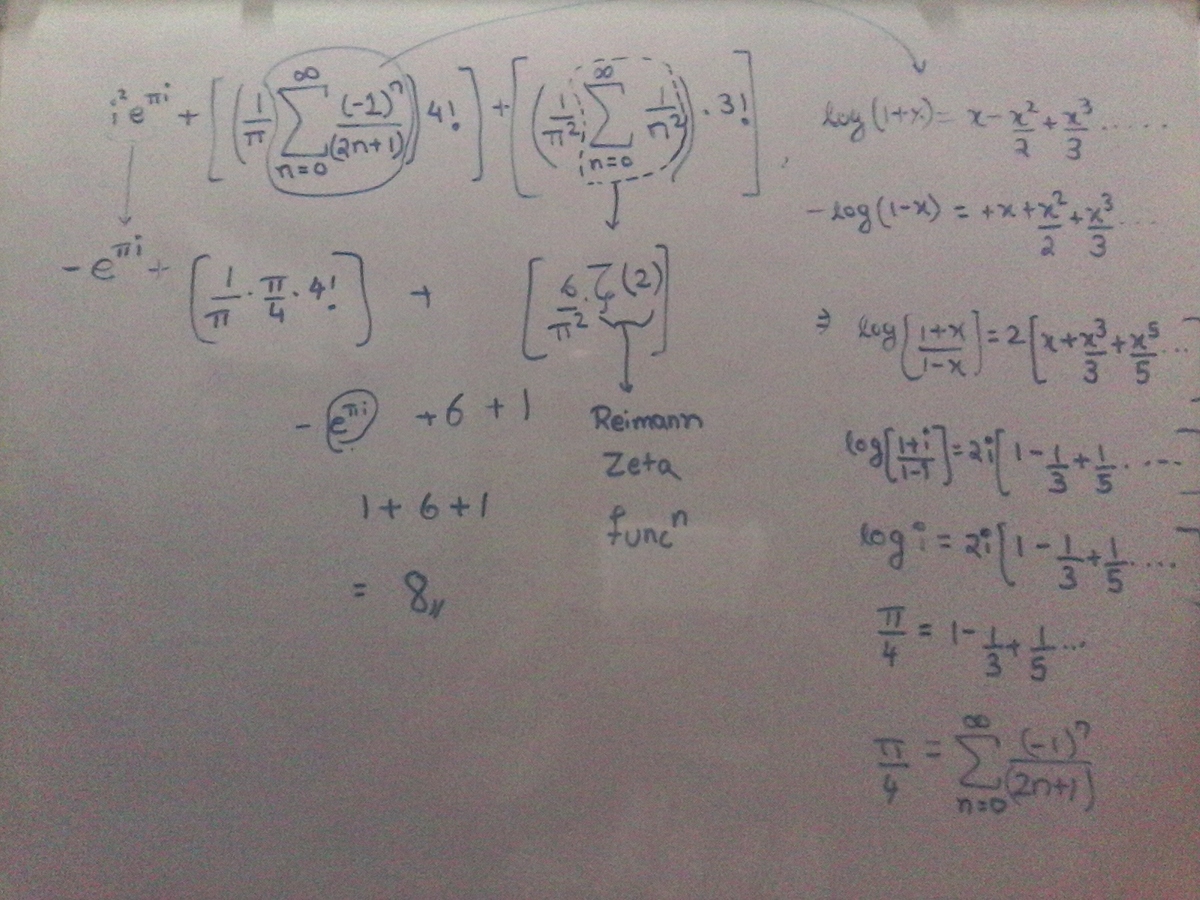I wish I could go to this hotel I did the part which looks difficult hope you all can do the rest and reach answer