It will take the heck out of you!!!
Find the radius of the circle of intersection of the sphere
x 2 + y 2 + z 2 − 2 x + 4 y − 2 0 = 0
by the plane
x + y + 3 z − 1 0 = 0
The answer is 3.74.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Phythagoras is best ! Nice question ! :D
 image
image
Log in to reply
Thanks for adding a pic. It would make my solution better! ⌣ ¨
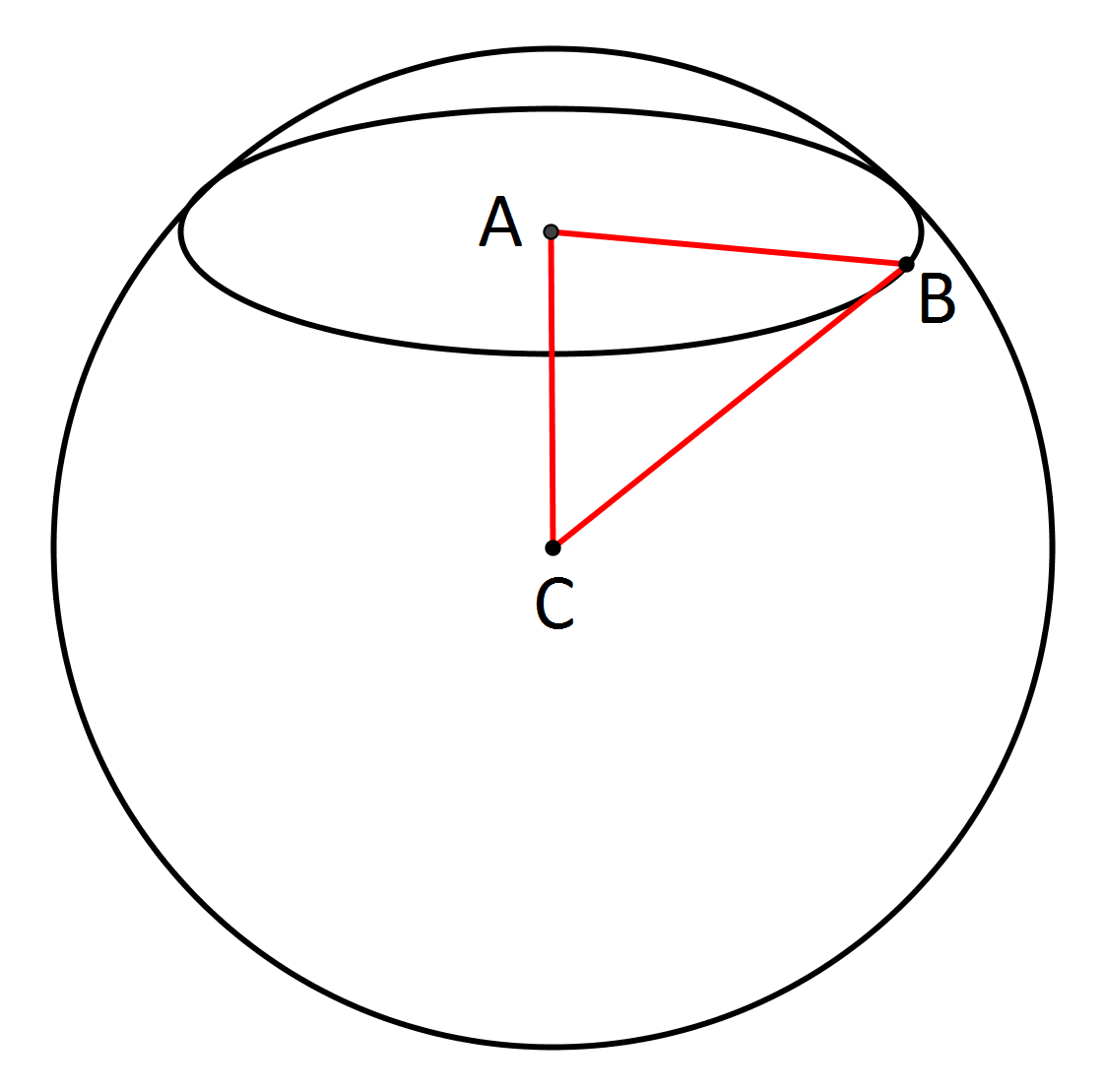
Centre of the sphere is ( 1 , − 2 , 0 ) and its radius is 5 units. And distance of point ( 1 , − 2 , 0 ) from plane x + y + 3 z − 1 0 = 0 is 1 1 units. So by Pythagoras Theorem, radius of circle is 5 2 − 1 1 = 1 4 = 3 . 7 4 1 6 units.
Highly Over-rated Question
Find distance of centre from plane and apply Pythagoras to get radius of cross section.
Please elaborate
The equation of sphere can be re-written as ( x − 1 ) 2 + ( y + 2 ) 2 + z 2 = 5 2
Therefore, centre of sphere is ( 1 , − 2 , 0 ) and radius is 5 .
The distance of point ( x 0 , y 0 , z 0 ) from a plane a x + b y + c z + d = 0 can be calculated by ∣ ∣ ∣ ∣ a 2 + b 2 + c 2 a x 0 + b y 0 + c z 0 + d ∣ ∣ ∣ ∣
Substituting the values, we get distance between centre of sphere and plane is 1 1 .
Applying Pythagoras theorem, 5 2 = r 2 + 1 1 2 . Solving, r = 1 4 ≈ 3 . 7 4 .