It's a bit hazy
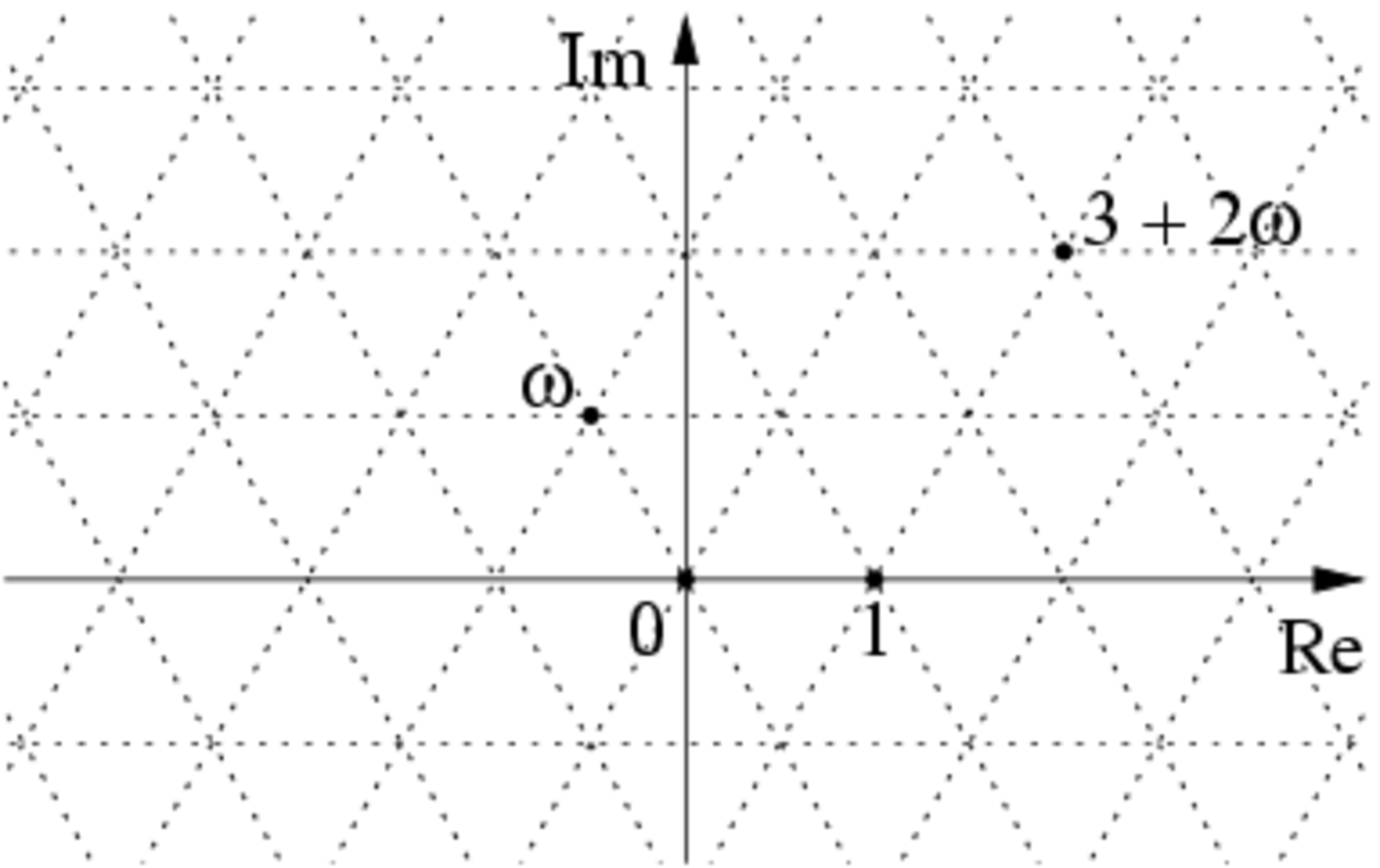
What is the probability an Eisenstein integer is visible from the origin (that is, a line from the origin to the integer does not intersect any other Eisenstein integers)?
Note: An Eisenstein integer is a complex number of the form a + b ω where ω = 2 − 1 + i 3 and a , b ∈ Z . For example, 1 , ω and 3 + 2 ω are all Eisenstein integers.
The answer is 0.607927101854.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Two distinct primes p and q are always relatively prime, (p,q)=1, as are any positive integer powers of distinct primes p and q, (p^m,q^n)=1.
Relative primality is not transitive. For example, (2,3)=1 and (3,4)=1, but (2,4)=2.
The probability that two integers m and n picked at random are relatively prime is
P((m,n)=1)=[zeta(2)]^(-1)=6/(pi^2)=0.60792...
Jake Lai, it's probably a good idea to include a short definition of an Eisenstein integer in your problem statement.
Will do. Thanks for the suggestion!
The probability that two random numbers are pairwise coprime is π 2 6 .This can be shown by using the fact that the partial sums of ϕ ( n ) are π 2 3 x 2 + O ( x l o g x ) .By the way @JakeLai , from what book are you getting these problems from?
And also, don't you mean a `gaussian integer(a+bi) in the complex plane, not an Eisenstein integer (the field a + b ϱ ) .
I just made this one myself. You got the problem kind of right; the Eisenstein case is isomorphic to the Gaussian case. You can just "slide" each n th row a bit to the right proportional to n .
Log in to reply
So where did you learn about this?I learned about the partial sums in a book for number theory.And what us the intended solution and interpretation?
Log in to reply
It's just to notice that you can "slide" each rows to the right. The Gaussian case is well-lnown, but here a quick proof:
The probabilty that two integers share a certain prime factor p is p 1 × p 1 = p − 2 . The probability they are coprime (equivalent to visibilty) is the complement, ie 1 − p − 2 . Take the product over all primes p and you get the Euler product for ζ ( 2 ) 1 .
I learnt about this while researching the Riemann zeta function online.
How do we solve this? It's just to notice that you can just "slide" each n th row a bit to the right (or left, if you like) proportional to n to obtain something resembling the Gaussian integers. The Gaussian case is well-known, but here a quick proof:
The probability that two integers share a certain prime factor p is p 1 × p 1 = p − 2 . The probability they are coprime (equivalent to visibilty) is the complement, ie 1 − p − 2 .
Take the product over all primes p and you get the Euler product
p prime ∏ ( 1 − p − 2 ) = ζ ( 2 ) 1 ≈ 0 . 6 0 8