It's A Factor of 24
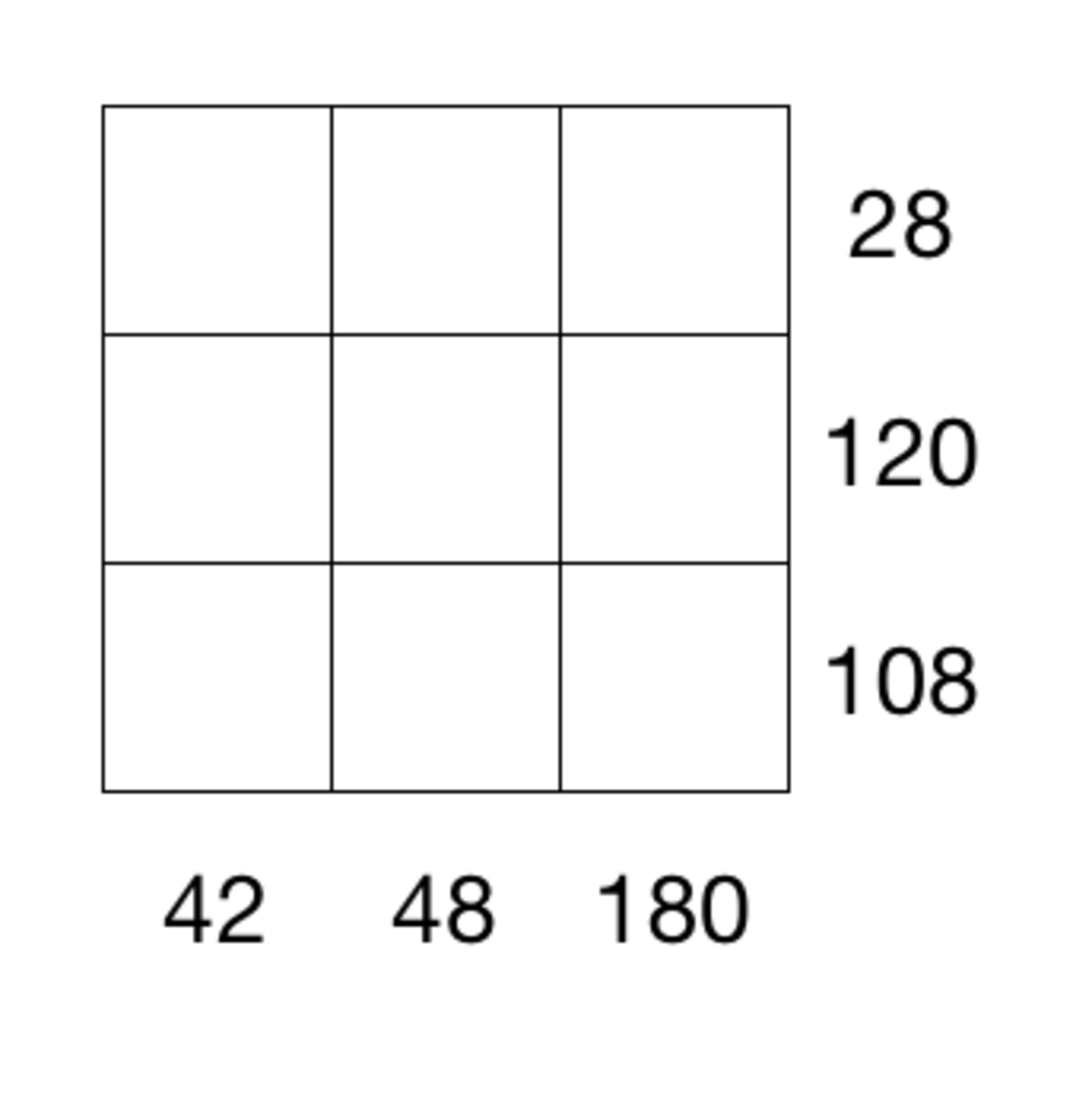
In the 3 by 3 square, we place distinct digits from 1 to 9. The number by each row and column indicates the product of these numbers.
What is the value of the center square?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.

The only way we can factor 2 8 using 3 distinct digits is some order of 1 × 4 × 7 , so these 3 digits lie in the first row. Now 7 is not a factor of either 4 8 or 1 8 0 , but is one of 4 2 , so 7 must go in the upper left box. Now for the first column, since 4 2 = 7 × 6 and since 1 has already been used in the first row, the lower two boxes in the first column must be 2 and 3 in some order.
Now we cannot have 1 in the upper right box since there are no two digits whose product is 1 8 0 , thus 1 must go in the middle of the upper row and thus 4 must be placed in the upper right box. The lower two boxes of the middle column must then be 6 and 8 in some order, as this is the only way to have a product of two digits be 4 8 . Next, since 1 8 0 = 4 × 4 5 and the only way to factor 4 5 using two digits is 5 × 9 , the lower two boxes of the rightmost column must be 5 and 9 in some order.
Next, as 9 is a factor of 1 0 8 but not 1 2 0 , we must place 9 in the lower right box. Then since 1 0 8 = 9 × 1 2 and 4 has already been used, we must have 2 and 6 in the first two boxes of the bottom row, which in turn then forces 3 and 8 , in that order, into the first two boxes of the middle row. Thus the digit 8 must be placed in the center box.
The completed grid looks like
7 1 4 2 8
3 8 5 1 2 0
2 6 9 1 0 8
4 2 4 8 1 8 0