It's a jelly bean!
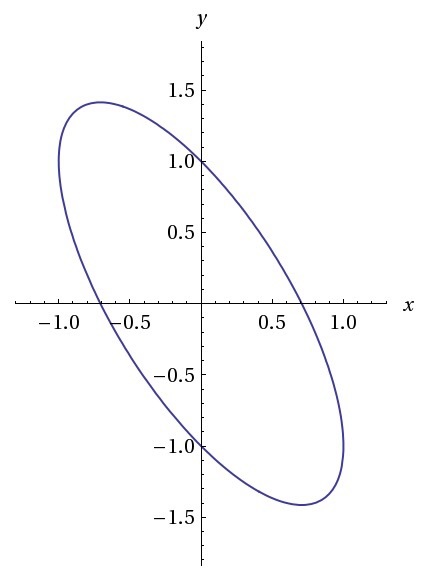
The graph above shows the figure created by the function x 2 + ( y + x ) 2 = 1 .
Find the area of this tilted ellipse correct to 2 decimal places.
The answer is 3.14.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
13 solutions
"Stupid"? I imagine that in earlier times many problems were solved along these lines.
Log in to reply
Sounds like a pun if you think about it
Log in to reply
I like puns but can't see this one. Do ellucidate!
All we need to do is to rotate the co-ordinate axes so that they coincide with the major and minor axes of the ellipse. This will render the ellipse in the standard form. But the beauty is that we don't even need to do all the calculations explicitly if we employ a tiny bit of linear algebra. First, notice that x 2 + ( y + x ) 2 = 2 x 2 + 2 x y + y 2 = z T A z where A = ( 2 1 1 1 ) and z = ( x y ) . Now let us write the eigen decomposition of A as A = U Λ U T where U is an orthonormal (rotation) matrix and Λ is a diagonal matrix consisting of eigenvalues of A . Since rotation does not change the area, we change the co-ordinates as follows ζ = U T z . With this transformation, the equation of the ellipse becomes ζ T Λ ζ = 1 However, since Λ is diagonal, the above is equivalent to λ 1 ζ 1 2 + λ 2 ζ 2 2 = 1 This is an ellipse in standard form and its area S is well-known to be S = λ 1 λ 2 π = det ( A ) π Thus all we need to do is to compute det ( A ) , which is 1 in this case and the answer follows.
What kind of magic is that?
(O.o)
Wat
@Brian Charlesworth this looks like a solution you would write XD lol
Very nice one! (As expected) This is exactly what I did.
Use only the geometry way to solve the problem with no trig and calculus:
Step 1: { x 2 + ( y + x ) 2 = 1 x 2 + y 2 = 1
Subtract the equations we have x ( 2 y + x ) = 0 .
First two solutions are obvious: A = ( 0 , 1 ) and B = ( 0 , − 1 ) . The other two solutions are C = ( 5 2 , − 5 1 ) , and D = ( − 5 2 , 5 1 ) .
Slope of line AD is m = − 2 1 + 5 .
The major axis of the ellipse (a) can be calculated from ⎩ ⎨ ⎧ x 2 + ( y + x ) 2 = 1 y = − 2 1 + 5 x
a = 2 5 + 1 .
The minor axis of the ellipse (b) can be calcuated from ⎩ ⎨ ⎧ x 2 + ( y + x ) 2 = 1 y = 1 + 5 2 x
b = 2 5 − 1 .
Therefore, the area of the ellipse is
A r e a = π a b = π 2 5 + 1 ⋅ 2 5 − 1 = π .
Since the figure is perfectly elliptical (can some one prove this?) if we make a circle of radius r centered at ( 0 , 0 ) such that it has only two solutions with the ellipse, the solutions for 2 r will be the lengths of the major and minor axes of the ellipse.
We have the equations
{ x 2 + ( y + x ) 2 = 1 y 2 + x 2 = r 2
Solving and plugging for y.
x 2 + ( r 2 − x 2 + x ) 2 = 1
Note that here the sign of the root doesn't matter here.
x 2 + r 2 + 2 x r 2 − x 2 = 1
4 x 2 r 2 − 4 x 4 = r 4 + x 4 + 1 + 2 x 2 r 2 − 2 x 2 − 2 r 2
0 = 5 x 4 − 2 x 2 ( r 2 + 1 ) + ( r 4 − 2 r 2 + 1 )
Messy quadratic (note there are no odd powers of x)
x = 5 r 2 + 2 − r 4 + 3 r 2 − 1 + 1
We need to check the extremes of this equation (Max and min r) such that x is still a real number.
Looking at the roots of the radical inside the radical (radicalception)
r 2 = 2 3 ± 5
R = 2 1 + 5 , r = 2 − 1 + 5
Where R is the major axis and r is the minor axis.
This the area is
R r π = 2 1 + 5 ⋅ 2 − 1 + 5 π = π
In the third line, does it suppose the equation y(2x+y)=0 be x(x+2y)=0?
Very nice! This is very similar to the pure geometric solution I had. I'll post the algebraic/geometric solution tonight if no one has posted it by then.
Let x = r cos θ , y = r sin θ Substitute this into the equation to get, r 2 ( 1 + cos 2 θ + 2 sin θ cos θ ) = 1 Now, we can put any value of θ and get r
So, first we minimize ( 1 + cos 2 θ + 2 sin θ cos θ ) to get semi-major axis by differentiating and equating to zero.
Similarly,we find semi-minor axis and the use the formula A = π a b
This will yield an approximation (which is very very close). But The minima and maxima of the function are not the end points of the major axis.
Same ... Best and shortest method ..!
should it be r^2 ( 1 + cos^2 + 2sin cos ) = 1 ???
Log in to reply
Yes ,you are correct.I have made edits to correct my solution.However,the answer remains same as the area of ellipse remains same even if it is rotated.
Let u = x , v = y + x . The Jacobian of the transformation from the x y -plane to the u v -plane is ∣ ∣ ∣ ∣ det ( 1 0 1 1 ) ∣ ∣ ∣ ∣ = 1 , so area is preserved. In the u v -plane, the ellipse is mapped to the unit circle given by u 2 + v 2 = 1 . Therefore, the area of the ellipse is π ≈ 3 . 1 4 .
Out of many interesting solutions, this is the best one.
The ellipse implicitly defined by the equation x 2 + ( x + y ) 2 = 1 can be described by the following parametric funtion γ ( t ) = ( c o s ( t ) , s i n ( t ) − c o s ( t ) ) with t ∈ [ 0 , 2 π ] . On other hand let F ( x , y ) = ( 0 , x ) be a vector field such as ∂ x ∂ F y − ∂ y ∂ F x = 1 so we can use the Green's Theorem:
∫ 0 2 π F ( γ ( t ) ) ⋅ γ ′ ( t ) d t = ∫ γ ∂ x ∂ F y − ∂ y ∂ F x d A
Replacing what we know in the above equation :
∫ 0 2 π ( 0 , c o s ( t ) ) ⋅ ( − s i n ( t ) , c o s ( t ) − s i n ( t ) ) d t = ∫ γ d A
∫ 0 2 π c o s 2 ( t ) − c o s ( t ) s i n ( t ) d t = A
We know that ∫ 0 2 π c o s 2 ( t ) d t = π and ∫ 0 2 π − c o s ( t ) s i n ( t ) d t = 0 then:
A = π
I resorted to Lagrange multipliers—something I can do symbolically for the most part.

I have absolutely no idea what the heck this is. But it looks smart :3 nice job none the less.
Log in to reply
Thank you. Nice problem. When I saw Lagrange multipliers 50 years ago I can't remember that the professor suggested anything that we could do with them.
I'm guessing this is some sort of minimization via Lagrange multipliers. The script just does the algebra .
Log in to reply
You're right. I'm quite sure that, even without knowing any Python, if you look at the detail you can see what's happening. It's probably of no interest to anyone who doesn't write code.
I didn't have a name for that but it was the most intuitive and simple for me!
Let x=sinA
x+y=cosA or y=cosA-sinA
Integrate ydx from 0 to 2(pi) to get solution as pi
Would you mind elaborating a bit?
There are many ways to solve the problem. I can think of at least 4. 2 of which require calculus, one of which uses algebra+geometry (I wouldn't go as far as to call it analytical geom), and one which uses purely coordinate geometry.
Trevor since you actually tagged it under #geometry can you pleade post the non-calculus ways.
P.s. Many like me still used calculus any way
Log in to reply
Refer to Alex Zhong's solution. I'll post the half Alg half geom solution tonight if no one has posted it by then.
I just posted the Alg-geom solution as a comment on Alex Zhong's solution
Another Solution,
x 2 + ( x + y ) 2 = 1 Let X and Y be the axis after rotation,
X Y x cos θ − sin θ y sin θ cos θ
x y x + y = X cos θ − Y sin θ = X sin θ + Y cos θ = X ( cos θ + sin θ ) + Y ( cos θ − sin θ )
To get X Y term = 0 ,
x 2 + ( x + y ) 2 = ⋯ − 2 X Y sin θ cos θ + ⋯ + 2 X Y ( cos 2 θ − sin 2 θ ) + ⋯ tan 2 θ = 2
Getting Ellipse Equation,
x 2 ( cos 2 θ + sin θ cos θ + 1 ) + y 2 ( sin 2 θ + 1 − sin θ cos θ ) = 1 ≡ a 2 x 2 + b 2 y 2
Putting values of θ ,
a 2 1 ⋅ b 2 1 = 1 ⇒ a b = 1
∴ A r e a = π a b = π
y = − x ± − x 2 + 1 Area = 2 ∫ − 1 1 1 − x 2 d x = π ( 1 ) 2
i just found the inersection by the line y=-x nd the r s we ll know is pi l b , l is mjor xis nd b is minor xis , you get pi .
I believe this solution is simpler...
Note that the graph is a circle, except each vertical slice is just translated up/down by some amount, determined by x. However, simply moving the slices shouldn't change the area. Thus, the area should still be that of a unit circle, or π .
Here is my stupid non-rigorous calculus approach. Consider a red vertical strip of area d A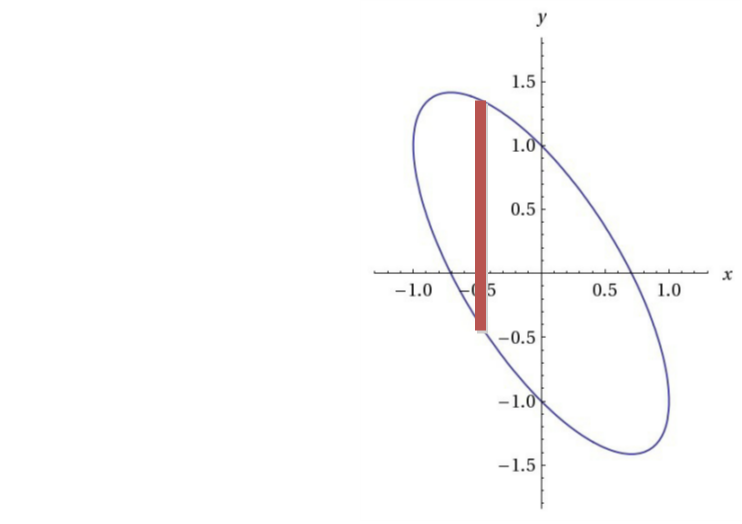 The length of this strip
D
can be found by solving for
y
. This is just the euclidean distance between points obtained by intersecting a vertical line at
x
(
x
,
1
−
x
2
−
x
)
,
(
x
,
−
1
−
x
2
−
x
)
thus the distance
D
=
2
1
−
x
2
. We know that the small area is just the the length times width of the strip
d
A
=
D
d
x
d
A
=
2
1
−
x
2
d
x
A
=
2
∫
−
1
1
1
−
x
2
d
x
=
π
The length of this strip
D
can be found by solving for
y
. This is just the euclidean distance between points obtained by intersecting a vertical line at
x
(
x
,
1
−
x
2
−
x
)
,
(
x
,
−
1
−
x
2
−
x
)
thus the distance
D
=
2
1
−
x
2
. We know that the small area is just the the length times width of the strip
d
A
=
D
d
x
d
A
=
2
1
−
x
2
d
x
A
=
2
∫
−
1
1
1
−
x
2
d
x
=
π