It's all about Areas!
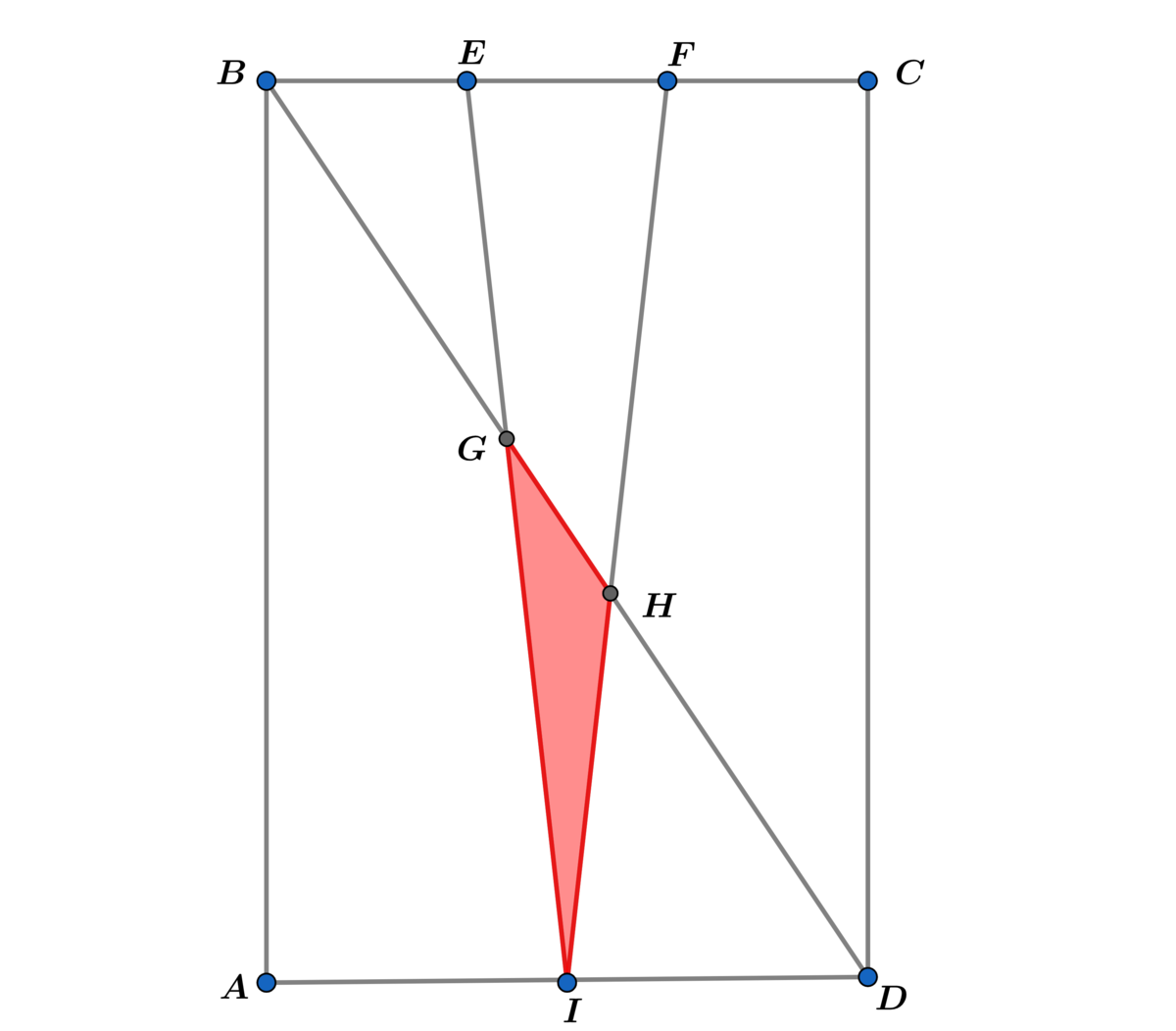
In rectangle A B C D with diagonal B D , let I be a midpoint of A D and let E I and F I trisect B C .
Let A R be the area of the red shaded region.
If A A B C D A R = β α , where α and β are coprime positive integers, find α + β .
The answer is 73.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
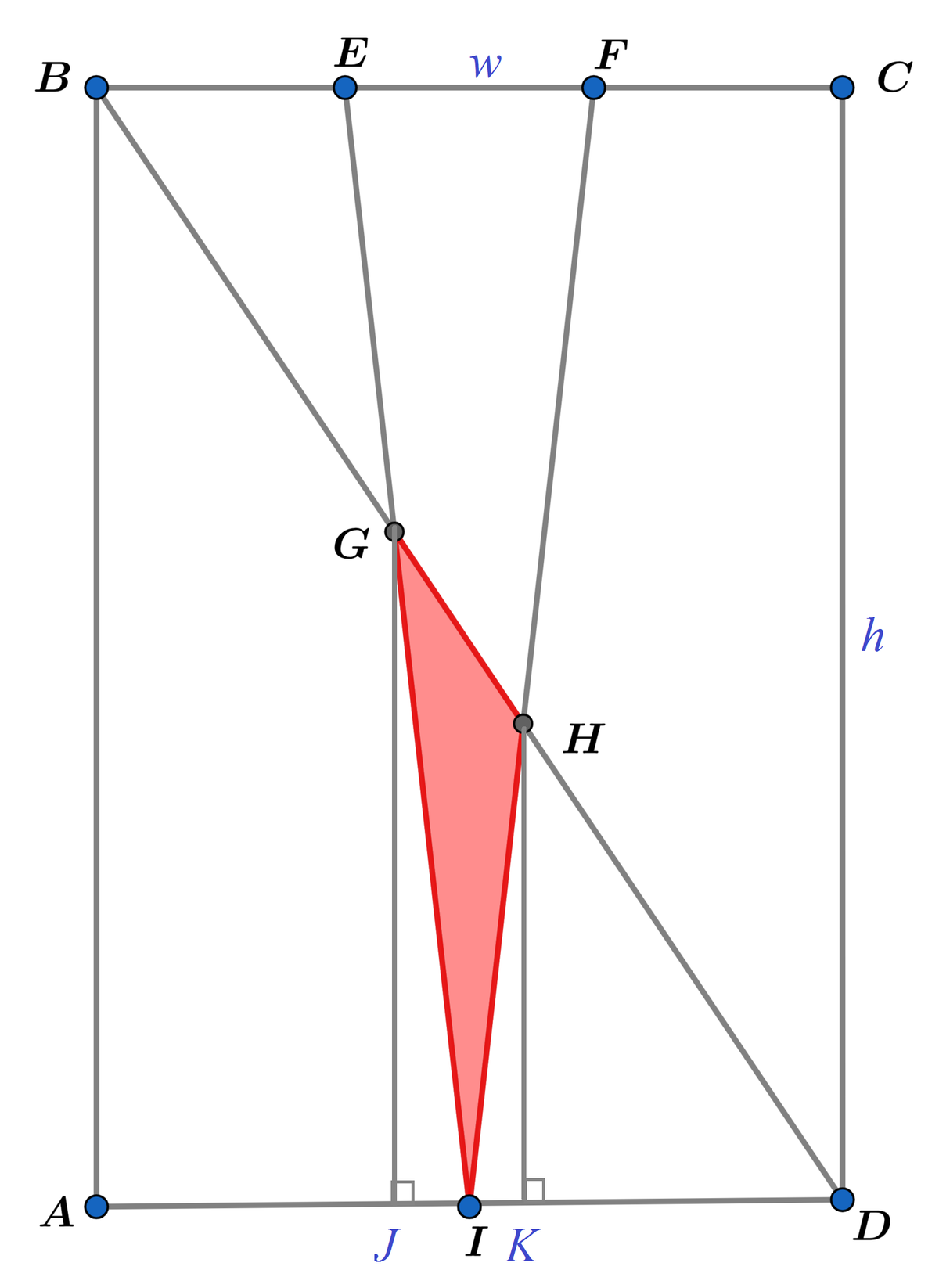
Let the width and height of rectangle A B C D be w and h respectively, and G J = h 1 and H K = h 2 are perpendicular to A D . We note that ∠ G I A = ∠ F I D = tan − 1 2 w − 3 w h = tan − 1 w 6 h and ∠ B D A = tan − 1 w h . Then we have:
J D G J ⋅ cot ∠ B D A h 1 ⋅ h w 6 h 5 h 1 ⟹ h 1 = J I + I D = G J ⋅ cot ∠ G I A + 2 w = h 1 ⋅ 6 h w + 2 w = 2 1 = 5 3 h
Similarly,
I D 2 w 2 w 2 1 ⟹ h 2 = I K + K D = H K ⋅ cot ∠ F I D + H K ⋅ cot ∠ B D A = h 2 ⋅ 6 h w + h 2 ⋅ h w = 6 h 7 h 2 = 7 3 h
Let the area of the rectangle [ A B C D ] = w h = 1 . Then [ H I D ] = 2 1 ⋅ 2 w ⋅ 7 3 h = 2 8 3 , [ B E G ] = 2 1 ⋅ 3 w ( h − 5 3 h ) = 1 5 1 , and
[ G H I ] ⟹ [ A B C D ] [ G H I ] = [ A B D ] − [ A B G I ] − [ H I D ] = 2 1 w h − ( [ A B E I ] − [ B E G ] ) − 2 8 3 = 2 1 − ( 2 3 w + 2 w ⋅ h − 1 5 1 ) − 2 8 3 = 2 1 − 1 2 5 + 1 5 1 − 2 8 3 = 7 0 3 = 7 0 3
Therefore α + β = 3 + 7 0 = 7 3 .
I wanted to see if sympy could do the algebra for the general case, and almost got there, but ran into a python error I could not resolve, so I settled for a specific 3x2 rectangle. Here is an interactive demo of how the area ratio remains constant for the general rectangle. Just move the sliders.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
|
1 2 |
|
why is this ignored?
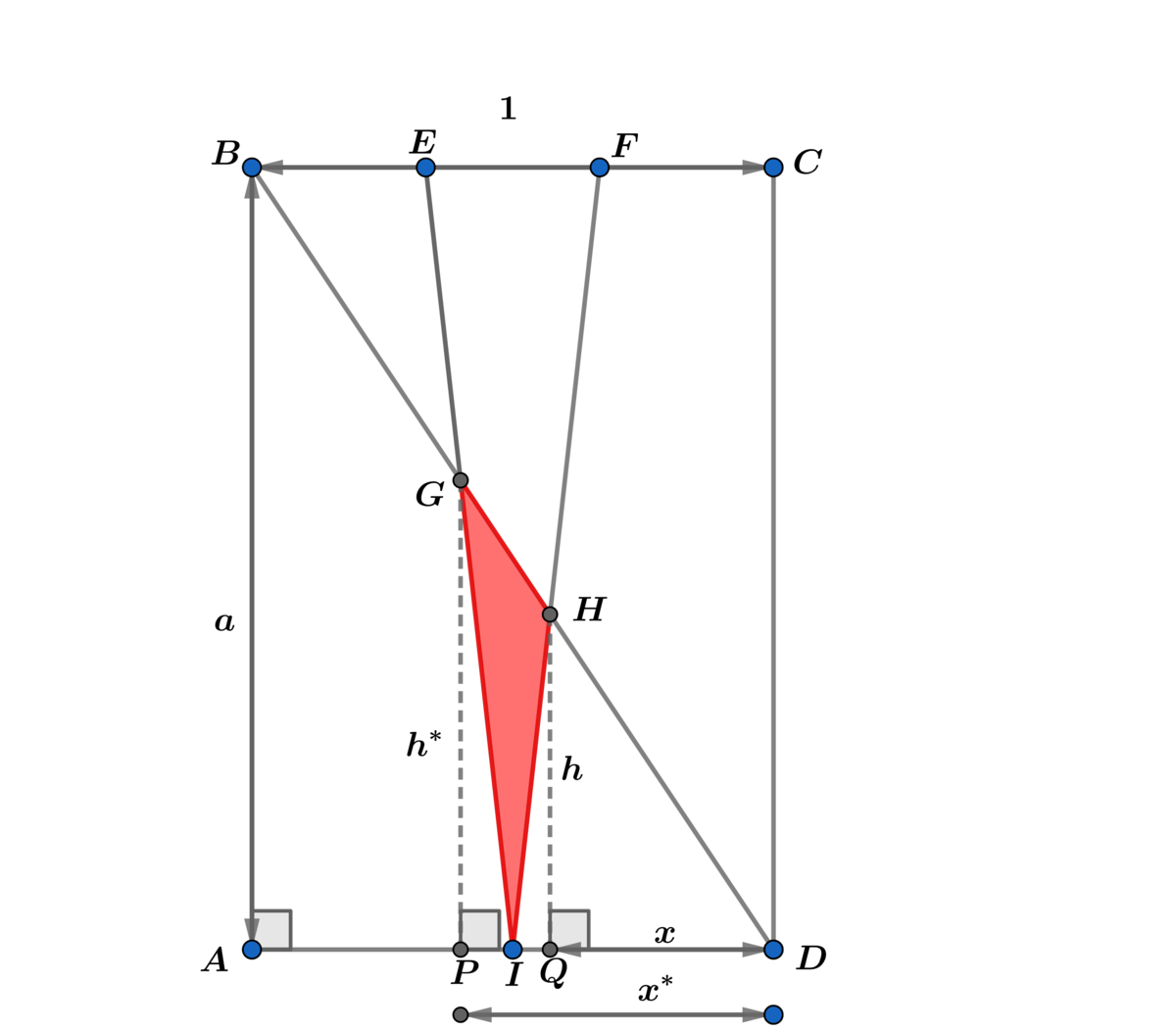
Let A A B C D = a with B C = 1 and A B = a
First we will obtain h ∗ and h using △ B E G ∼ △ I G D and △ B F H ∼ △ H I D , then using the diagram above with △ G P D ∼ △ A B D and △ H Q D ∼ △ A B D we obtain x ∗ and x .
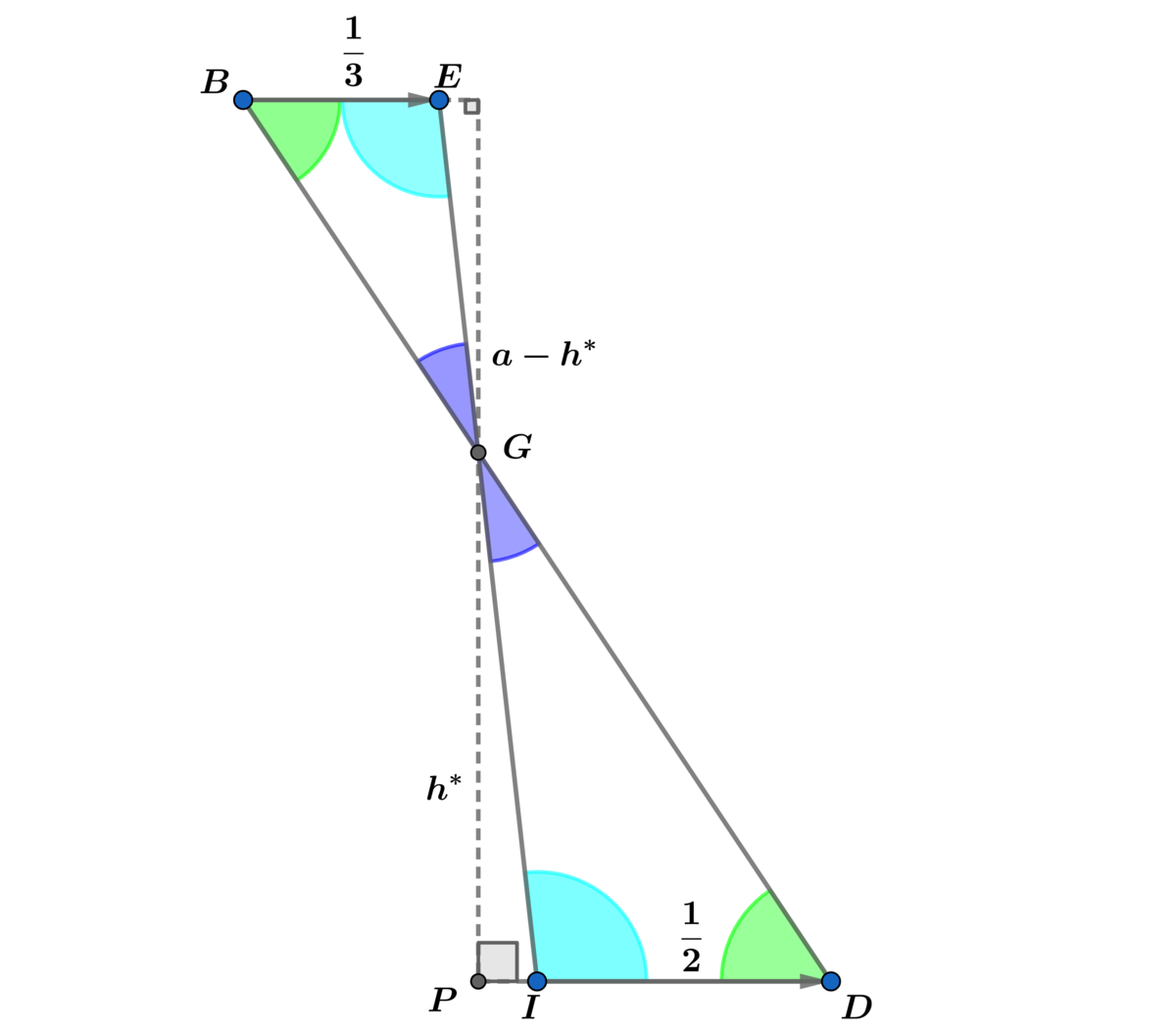
a − h ∗ h ∗ = 3 1 2 1 = 2 3 ⟹ 2 h ∗ = 3 a − 3 h ∗ ⟹ h ∗ = 5 3 a
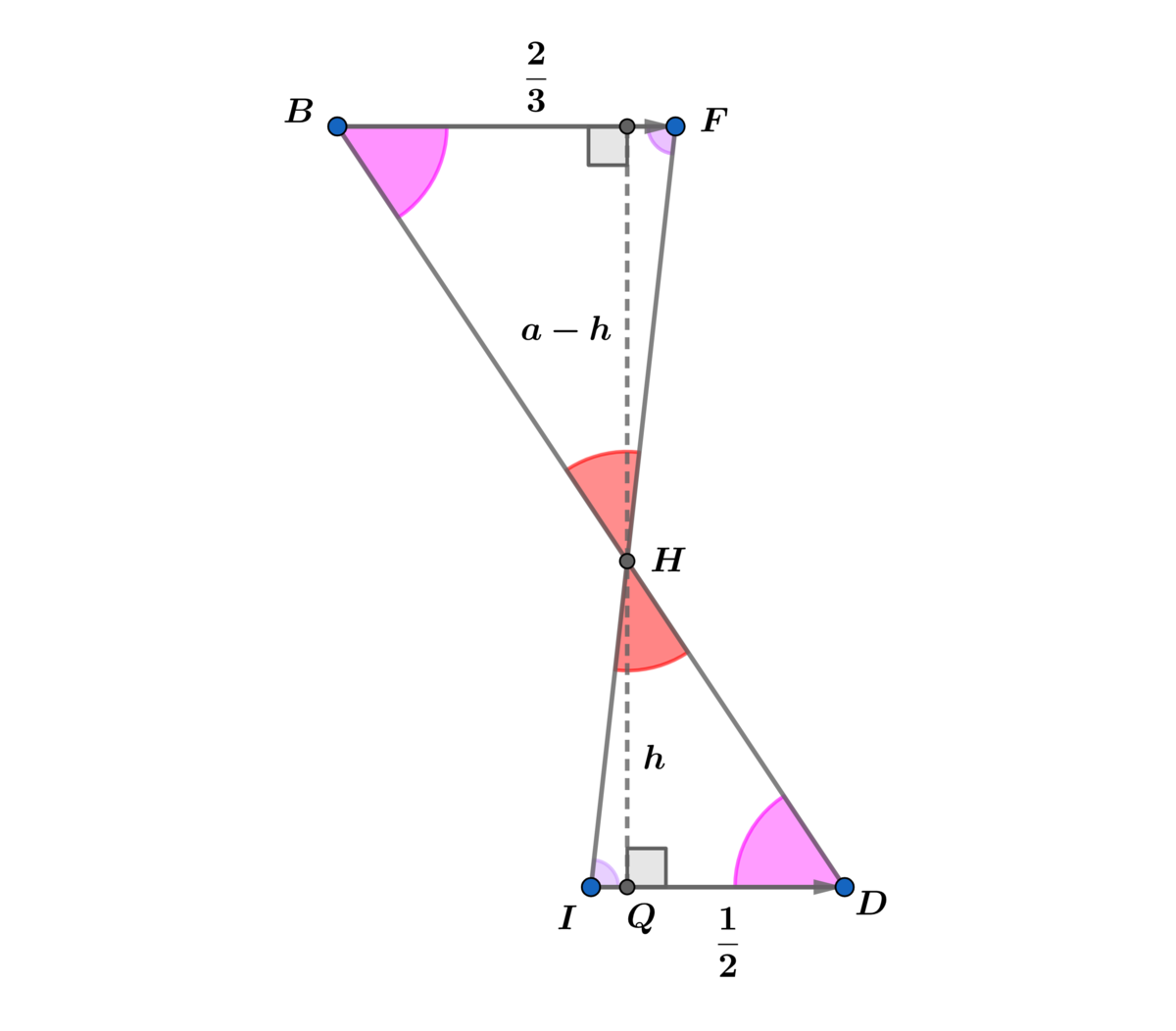
a − h h = 3 2 2 1 = 4 3 ⟹ 4 h = 3 a − 3 h ⟹ h = 7 3 a
Using △ G P D ∼ △ A B D ⟹ h ∗ a = x ∗ 1 ⟹ a x ∗ = h ∗ = 5 3 a ⟹ x ∗ = 5 3 .
Using △ H Q D ∼ △ A B D ⟹ h a = x 1 ⟹ a x = h = 7 3 a ⟹ x = 7 3
A P = 1 − 5 3 = 5 2 ⟹ P I = 2 1 − 5 2 = 1 0 1 ⟹
A △ G P I = 2 1 P I h ∗ = 2 1 ( 1 0 1 ) ( 5 3 a ) = 1 0 0 3 a
and
A △ H I D = 2 1 ( 2 1 ) h = 4 1 ( 7 3 a ) = 2 8 3 a
and
A △ G P D = 2 1 x ∗ h ∗ = 2 1 ( 5 3 ) ( 5 3 a ) = 5 0 9 a
⟹
A R = A △ G P D − ( A △ H I D + A △ G P I ) = 5 0 9 a − ( 2 8 3 a + 1 0 0 3 a ) = ( 5 0 9 − 1 7 5 2 4 ) a =
7 0 3 a ⟹ A A B C D A R = 7 0 3 = β α ⟹ α + β = 7 3 .
Below is an alternative approach using coordinate geometry:
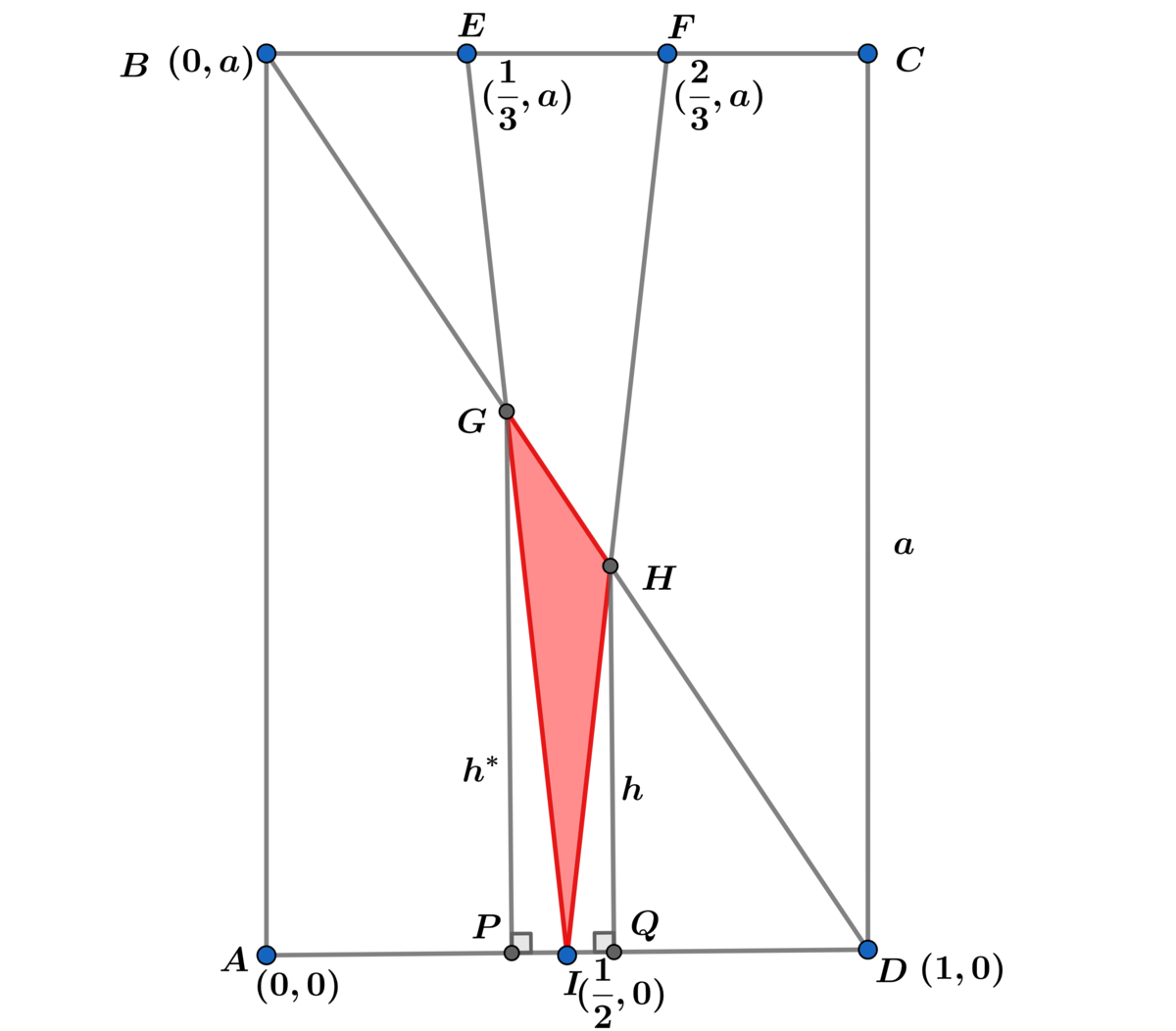
Let A A B C D = a with B C = 1 and C D = a
m F I = 6 a ⟹ y = 3 a ( 2 x − 1 )
m B D = − a ⟹ y = − a ( x − 1 )
⟹ 3 ( 2 x − 1 ) = − ( x − 1 ) ⟹ 6 x − 3 = − x + 1 ⟹ x = 7 4 ⟹
y = 7 3 a = h ⟹ H ( 7 4 , 7 3 a )
m E I = − 6 a ⟹ y = − 3 a ( 2 x − 1 )
B D y = − a ( x − 1 )
⟹ 3 a ( 2 x − 1 ) = a ( x − 1 ) ⟹ 6 x − 3 = x − 1 ⟹ x = 5 2 ⟹ y = 5 3 a = h ∗
⟹ G ( 5 2 , 5 3 a )
P I = 2 1 − 5 2 = 1 0 1 and I Q = 7 4 − 2 1 = 1 4 1
⟹ A △ H I Q = 2 1 ( 1 4 1 ) ( 7 3 a ) = 1 9 6 3 a
and
A △ G P I = 2 1 ( 1 0 1 ) ( 5 3 a ) = 1 0 0 3 a
and
A P Q H G = 2 1 ( 7 3 a + 5 3 a ) ( 1 0 1 + 1 4 1 ) = 2 3 a ( 3 5 1 2 ) ( 7 0 1 2 ) = 4 9 0 0 4 3 2 a = 1 2 2 5 1 0 8 a
⟹ A R = A P Q H G − ( A △ H I Q + A △ G P I ) = ( 1 2 2 5 1 0 8 − ( 1 9 6 3 + 1 0 0 3 ) ) a =
( 1 2 2 5 1 0 8 − 2 4 5 0 1 1 1 ) a = 7 0 3 a ⟹ A A B C D A R = 7 0 3 = β α ⟹ α + β = 7 3
.
Without the loss of generality, let the dimensions of this rectangle be h × 6 . Then plot this figure onto the Cartesian plane.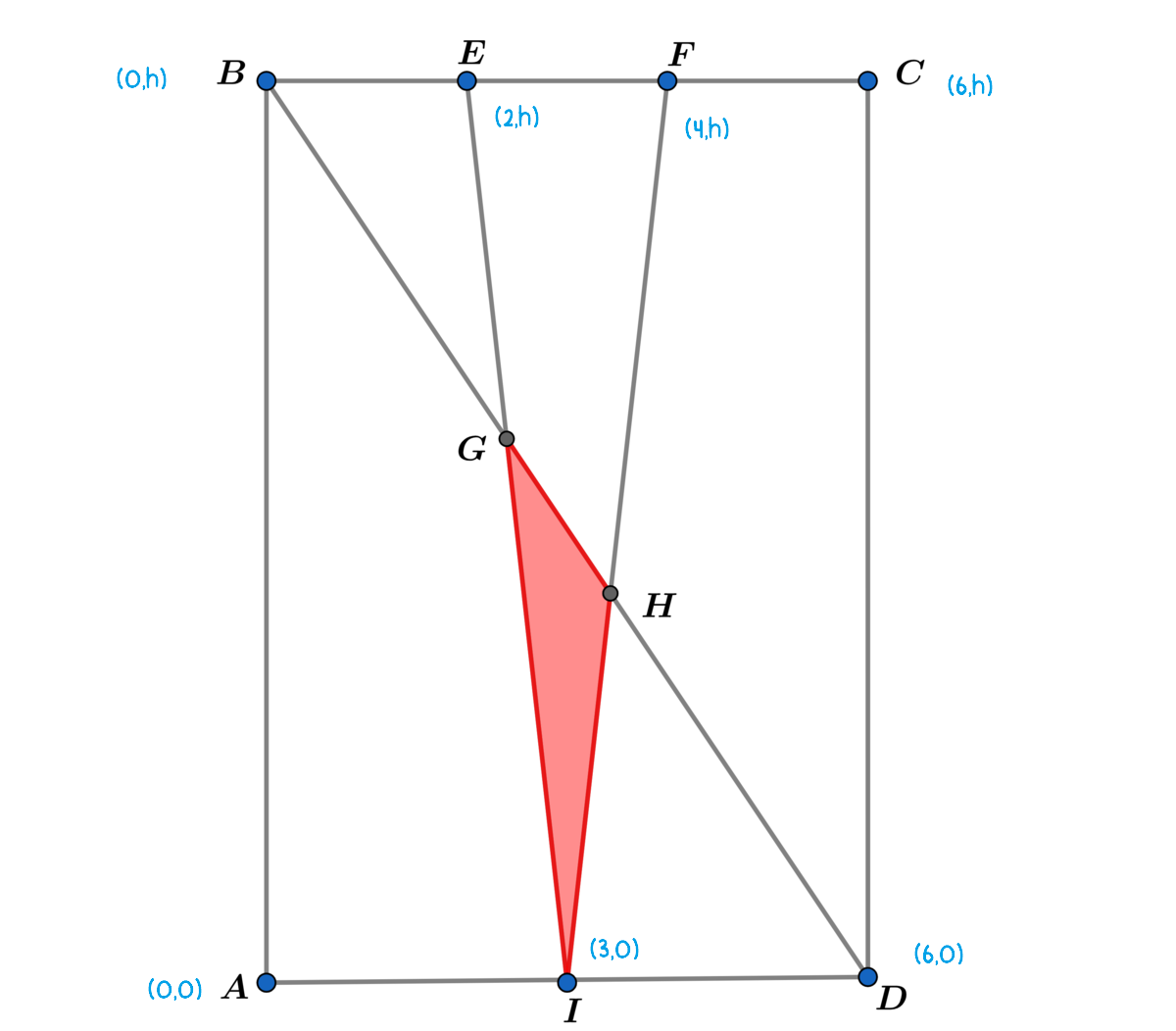 The equation of the straight line
B
D
is
x
/
6
+
y
/
h
=
1
.
The equation of the straight line
E
I
is
x
−
3
y
−
0
=
2
−
3
h
−
0
⇔
y
=
−
h
(
x
−
3
)
.
Likewise, the equation of the straight line
E
F
is
x
−
3
y
−
0
=
4
−
3
h
−
0
⇔
y
=
h
(
x
−
3
)
.
The coordinate of
G
is simply the intersection point of the straight lines
B
D
and
E
I
. In other words, we need to solve a system of equations
{
x
/
6
+
y
/
h
=
1
y
=
−
h
(
x
−
3
)
⟹
G
=
(
1
2
/
5
,
3
h
/
5
)
Analogously, we get
H
=
(
2
4
/
7
,
3
h
/
7
)
.
Using the shoelace formula, the area of the triangle
G
H
I
is:
2
1
∣
∣
∣
∣
3
0
2
4
/
7
3
h
/
5
1
2
/
5
3
h
/
7
3
0
∣
∣
∣
∣
=
2
1
[
(
5
9
h
+
3
5
3
6
h
)
−
(
3
5
7
2
h
+
7
9
h
)
]
=
3
5
9
h
Since the area of the rectangle is
6
h
, the ratio in question is
3
5
9
h
÷
6
h
=
7
0
3
. The answer is
3
+
7
0
=
7
3
.
The equation of the straight line
B
D
is
x
/
6
+
y
/
h
=
1
.
The equation of the straight line
E
I
is
x
−
3
y
−
0
=
2
−
3
h
−
0
⇔
y
=
−
h
(
x
−
3
)
.
Likewise, the equation of the straight line
E
F
is
x
−
3
y
−
0
=
4
−
3
h
−
0
⇔
y
=
h
(
x
−
3
)
.
The coordinate of
G
is simply the intersection point of the straight lines
B
D
and
E
I
. In other words, we need to solve a system of equations
{
x
/
6
+
y
/
h
=
1
y
=
−
h
(
x
−
3
)
⟹
G
=
(
1
2
/
5
,
3
h
/
5
)
Analogously, we get
H
=
(
2
4
/
7
,
3
h
/
7
)
.
Using the shoelace formula, the area of the triangle
G
H
I
is:
2
1
∣
∣
∣
∣
3
0
2
4
/
7
3
h
/
5
1
2
/
5
3
h
/
7
3
0
∣
∣
∣
∣
=
2
1
[
(
5
9
h
+
3
5
3
6
h
)
−
(
3
5
7
2
h
+
7
9
h
)
]
=
3
5
9
h
Since the area of the rectangle is
6
h
, the ratio in question is
3
5
9
h
÷
6
h
=
7
0
3
. The answer is
3
+
7
0
=
7
3
.