It's all about zeros

Number Theory Level 3

Find the trailing number of zeros of the decimal representation of $100! \times200! \times300! \times400! \times 500! .$

Notation: $!$ is the factorial notation. For example, $8! = 1\times2\times3\times\cdots\times8$ .

The answer is 370.

2 solutions

Ethan Mandelez
Mar 30, 2021

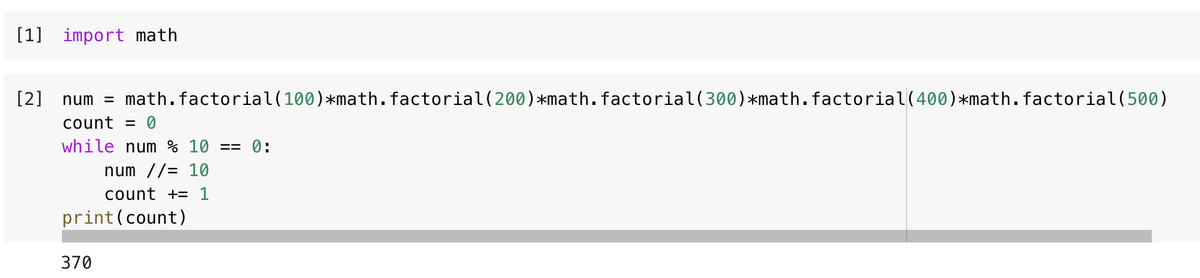
We find the number of trailing zeros in each of the factorials separately.

One could consider, how many factors of $5$ s are there in $100!$ ?

In $100!$ there are $24$ trailing zeros (i.e. There are $24$ factors of $5$ , namely $5$ , $10$ , $15$ , ..., $95$ , $100$ , however in $25$ , $50$ , $75$ and $100$ they contain another factor of $5$ ).

Similarly In $200!$ there are $49$ trailing zeros. $300!$ has $74$ trailing zeros, $400!$ has $99$ trailing zeros and $500!$ has $124$ trailing zeros.

Since they are multiplied together, we just need to add the number of trailing zeros in each factorial:

$24 + 49 + 74 + 99 + 124 = 370$ . Hence the final answer is 370

What if the digits immediately in front of the trailing zeros have a product of zero? (For example, 200 x 50 = 10000). I think you also need to show that multiplying these digits also do not end in zero.

David Vreken - 2 months, 1 week ago

Elijah Frank
Mar 31, 2021

It's all about zeros

The answer is 370.

2 solutions

0 pending reports