It's All Angles.
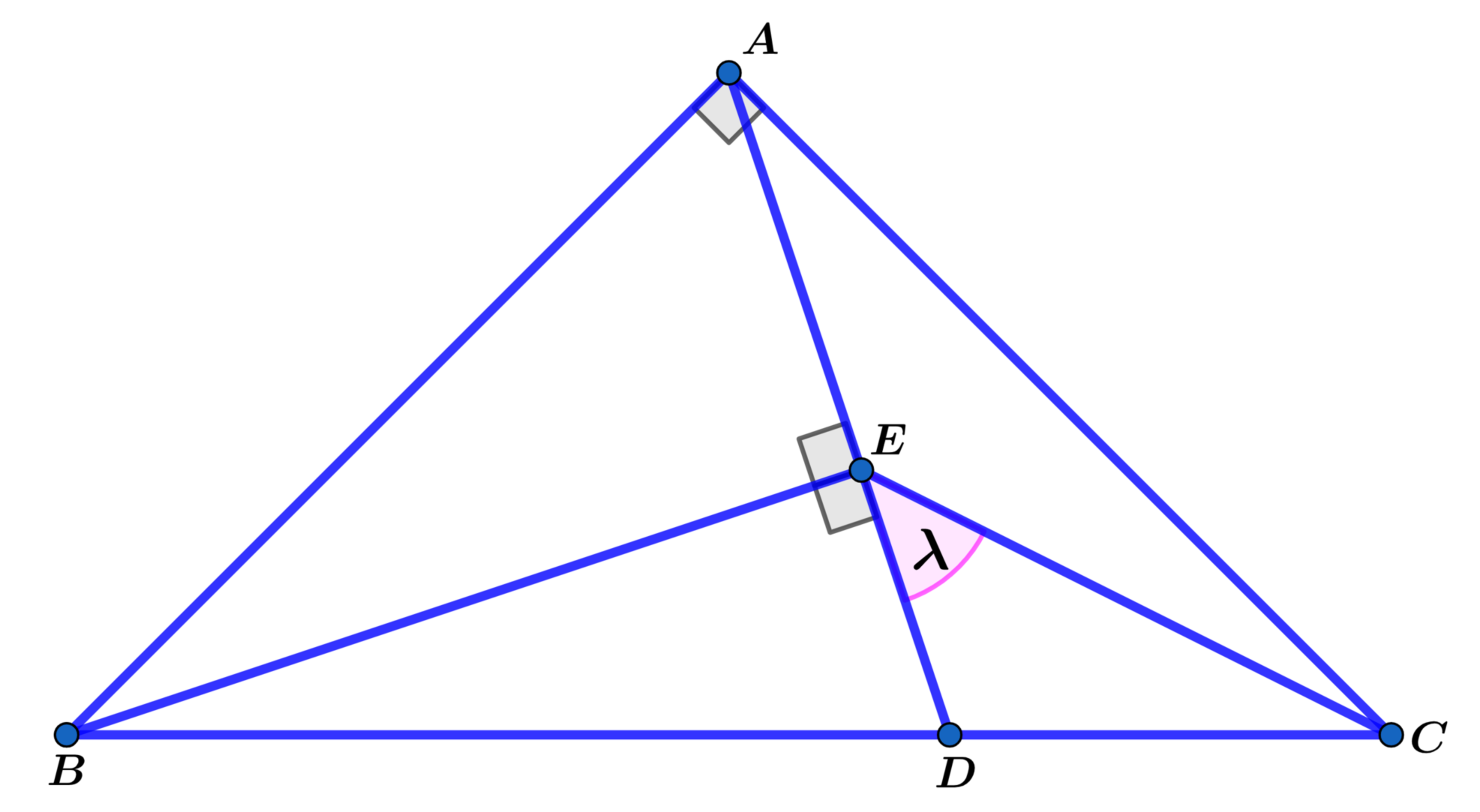
In isosceles right △ A B C , B D = 2 D C and ∠ A E B and ∠ B E D are right angles. Find angle λ (in degrees).
The answer is 45.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Another purely geometric solution, nice job!
Well done!
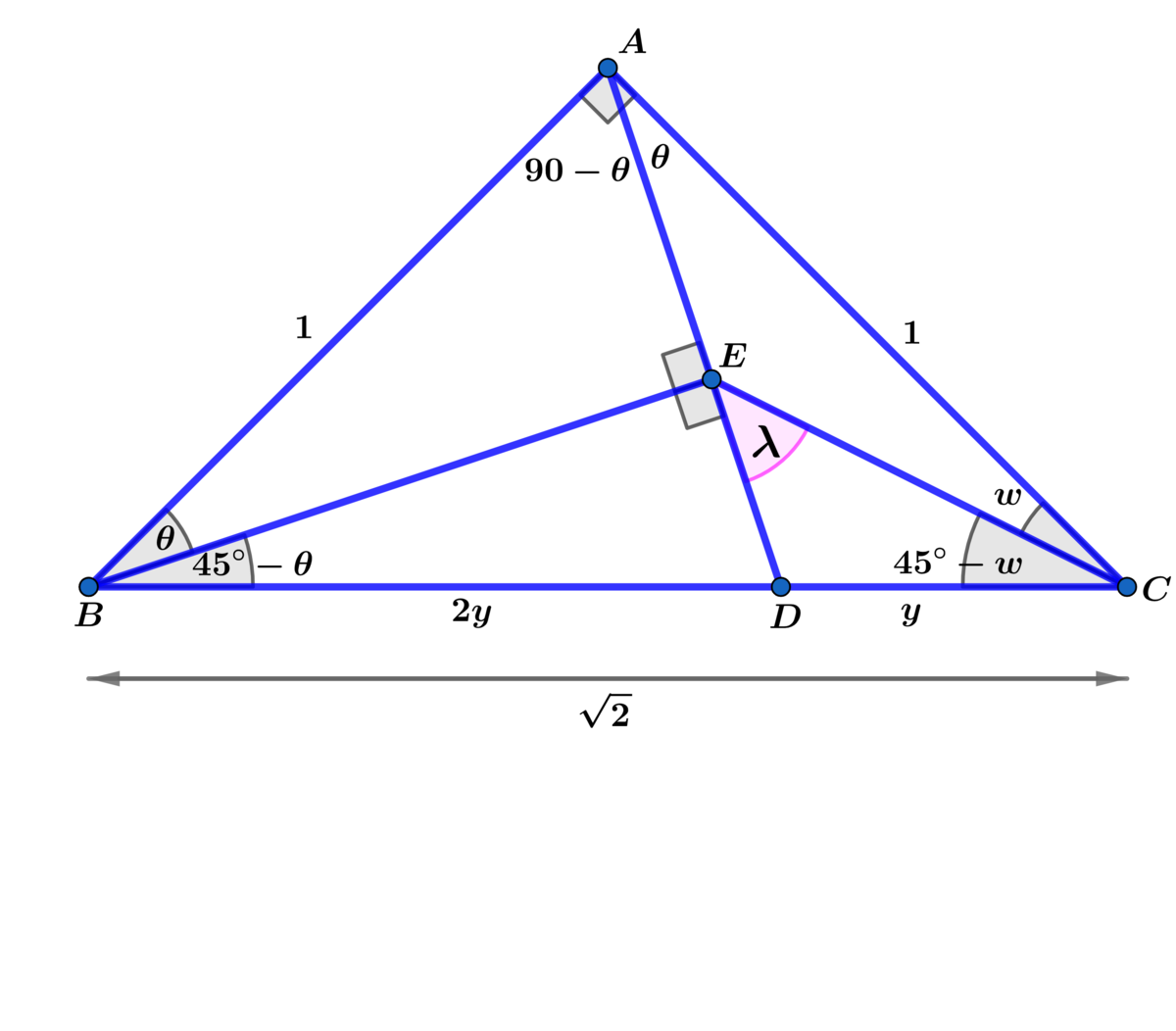
Let A B = A C = 1 ⟹ B C = 2 ⟹ .
Using the above diagram B C = 2 = 3 y ⟹ y = 3 2 ⟹ B D = 3 2 2 and using
△ B E C ⟹ 4 5 ∘ − θ + 9 0 ∘ + α + 4 5 ∘ − w = 1 8 0 ∘ ⟹ λ = θ + w .
Using the law of cosines on △ A B D with included angle 9 0 ∘ − θ ⟹
A D 2 = 1 + 9 8 − 3 4 2 ( 2 1 ) ⟹ A D = 3 5 ⟹
9 8 = 1 + 9 5 − 3 2 5 sin ( θ ) ⟹ sin ( θ ) = 5 1 = A E ⟹
B E = cos ( θ ) = 5 2 ⟹ E D = 3 5 − 5 1 = 3 5 2
Using the law of cosines on △ A E C with included angle θ ⟹
E C 2 = 1 + 5 1 − 5 4 = 5 2 ⟹ E C = 5 2 ⟹
5 1 = 1 + 5 2 − 5 2 2 cos ( w ) ⟹ cos ( w ) = 1 0 3 ⟹ sin ( w ) = 1 0 1
⟹ cos ( λ ) = cos ( θ + w ) = 5 2 1 0 3 − 5 1 1 0 1 = 1 0 5 = 2 1
⟹ λ = 4 5 ∘
Draw altitude A F intersecting B E at G , and let B F = A F = F C = 3 so that F D = 1 and D C = 2 :
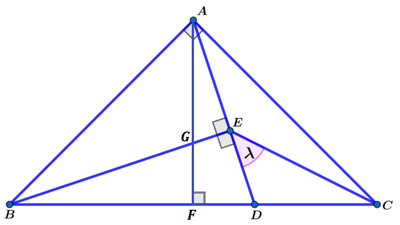
Then △ B F G ∼ △ B E D by AA similarity, and △ B E D ∼ △ A F D by AA similarity, and △ A F D ∼ △ A E G by AA similarity, so that all four triangles △ B F G ∼ △ B E D ∼ △ A F D ∼ △ A E G .
Since B F = A F and △ B F G ∼ △ A F D , △ B F G ≅ △ A F D , which means G F = F D = 1 . Then A G = A F − G F = 3 − 1 = 2 .
Let x = G E . Since △ A E G ∼ △ A F D , A E = E G ⋅ F D A F = x ⋅ 1 3 = 3 x .
Since △ A E G ∼ △ B E D , E D = B D ⋅ A G G E = 4 ⋅ 2 x = 2 x .
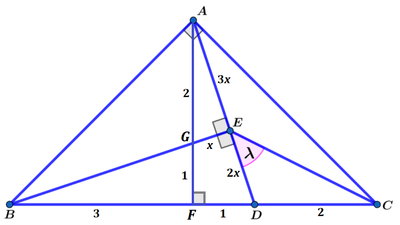
Now copy and rotate △ A F C and everything in it 9 0 ° clockwise about F :
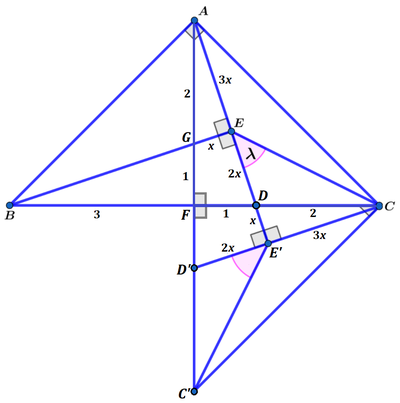
Then △ C E E ′ is an isosceles right triangle, so ∠ C E E ′ = λ = 4 5 ° .
Nice, purely geometric solution!
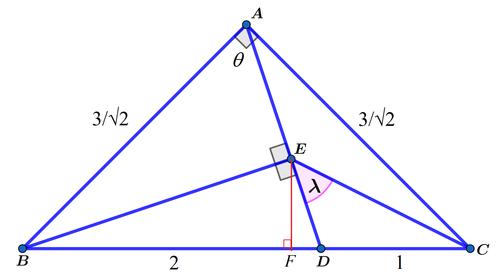
Let D C = 1 . Then B D = 2 and A B = A C = 2 3 . Let ∠ B A D = θ . Then be angle bisector theorem:
A C sin ∠ D A C A B sin ∠ B A D sin ( 9 0 ∘ − θ ) sin θ cos θ sin θ ⟹ tan θ = C D B D = 1 2 = 2 = 2 Note that A B = A C
Then sin θ = 5 2 , cos θ = 5 1 , and B E = A B sin θ = 1 0 6 . Let E F be perpendicular to B C . Then
B F E F = B E ⋅ cos ( 4 5 ∘ − ( 9 0 ∘ − θ ) ) = B E ⋅ cos ( θ − 4 5 ∘ ) = 1 0 6 ( 2 1 ⋅ 5 1 + 2 1 ⋅ 5 2 ) = 1 . 8 = B E ⋅ sin ( θ − 4 5 ∘ ) = 1 0 6 ⋅ 1 0 1 = 0 . 6
And
λ tan λ ⟹ λ = ∠ F E C − ∠ F E D = tan ( ∠ F E C − ∠ F E D ) = 1 − tan ∠ F E C ⋅ tan ∠ F E D tan ∠ F E C − tan ∠ F E D = 1 + 2 ⋅ 3 1 2 − 3 1 = 1 = 4 5 ∘ Note that tan ∠ F E C = E F F C = 0 . 6 1 . 2 = 2 and tan ∠ F E D = E F F D = 0 . 6 0 . 2 = 3 1
△ A B D and △ A B D are similar, thus, A B C M = B D D C = 2 1 This gives C M = 2 A B = 2 s , i.e. M is the midpoint of C F .
△ A B N and △ A C M are right-angled, with one pair of congruent legs ( A B = A C ) and one pair of congruent acute angles ( ∠ A B N = ∠ C A M because they are acute angles with perpendicular sides). Hence, △ A B N ≅ △ A C M thus, A N = C M , i.e. . N is the midpoint of A C .
Since ∠ N C M = ∠ N E M = 9 0 ∘ , quadrilateral N C M E is cyclic, thus, ∠ C E M = ∠ C N M
But, N C = C M = 2 s and N C M = 9 0 ∘ , thus, △ N C M is isosceles right triangle, hence, ∠ C N M = 4 5 ∘
Consequently, ∠ λ = ∠ C N M = 4 5 ∘