It's All Areas!

To find the value of $\bf a$ rearrange the octagon as shown above and inscribe it in a square.

Using the diagram above $\implies 2x^2 = (a - 1)^2 \implies x - \dfrac{a - 1}{\sqrt{2}}$

and the area of the square $A_{s} = (a + \sqrt{2}(a - 1))^2 = ((1 + \sqrt{2})a - \sqrt{2})^2 =$

$(3 + 2\sqrt{2})a^2 - 2\sqrt{2}(1 + \sqrt{2}) a + 2$

and

The area of the four right triangles is $A_{T} = 4(\dfrac{1}{2})\dfrac{(a - 1) ^2}{2} = (a - 1)^2$

The area of the octagon is

$A_{c} = A_{s} - A_{T} = (3 + 2\sqrt{2})a^2 - 2\sqrt{2}(1 + \sqrt{2}) a + 2 - (a^2 - 2a + 1) = 13 + 12\sqrt{2}$

$2(1 + \sqrt{2})a^2 - 2(1 + \sqrt{2})a - 12(1 + \sqrt{2}) = 0 \implies$

$a^2 - a - 6 = 0 \implies (a - 3)(a + 2) = 0$ and $a \geq 0 \implies a = 3 \implies a - 1 = 2.$

Now to find the radius $r$ of the circle:

Using the diagram above we have:

$4\theta + 4\beta = 360^{\circ} \implies \theta + \beta = 90^{\circ} \implies \beta = 90^{\circ} = \theta$

and

Using law of cosines $\implies 9 = 2r^2(1 - \cos(\theta))$ and $4 = 2r^2(1 - \cos(\beta)) =$

$2r^2(1 - \sin(\theta)) \implies 2r^2 = \dfrac{4}{1 - \sin(\theta)} = \dfrac{9}{1 - \cos(\theta)}$

$4 - 4\cos(\theta) = 9 - 9\sin(\theta) \implies 5 + 4\cos(\theta) = 9\sin(\theta) \implies$

$(5 + 4\cos(\theta))^2 = 81\sin^2(\theta) = 81 - 81\cos^2(\theta) \implies$

$97\cos^2(\theta) + 40\cos(\theta) - 56 = 0 \implies \cos(\theta) = \dfrac{-20 \pm 54\sqrt{2}}{97}$

$(0 < \theta < 90^{\circ}) \implies \cos(\theta) > 0 \implies \cos(\theta) = \dfrac{-20 + 54\sqrt{2}}{97}$

$\implies r = \dfrac{3}{\sqrt{2(1 - \cos(\theta))}}$ and using the above value of $\cos(\theta) \implies$

$r = \sqrt{\dfrac{97}{26 - 12\sqrt{2}}} = \implies$ the area of the circle $A = \dfrac{97}{26 - 12\sqrt{2}}\pi = \dfrac{\alpha}{\beta - \lambda\sqrt{\omega}}\pi$

$\implies \alpha + \beta + \lambda + \omega = \boxed{137}$ .

Just to explain more on @Chris Lewis ' solution for the benefits of those who may not understand.

Instead of four consecutive isosceles triangles of base length $a$ and four consecutive isosceles triangles of base length $a-1$ , we can place alternatively an $a$ -base triangle and an \(a-1)-base triangle to form the chipped-corners-square octagon as done by @Rocco Dalto . Rearranging the eight triangles of the octagon does not affect the area of the octagon \(13+12\sqrt 2\) and the circumradius $r$ , which we need to find.

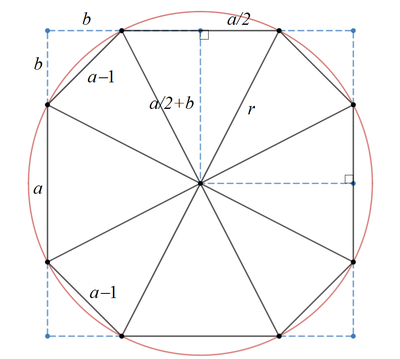
Let the leg length of the chipped off right isosceles triangles be $b$ as shown in the figure. Then the area of the octagon is:

$\begin{aligned} (a+2b)^2 - 4\cdot \frac {b^2}2 & = 13 + 12 \sqrt 2 \\ a^2 + 4a\blue b + 2\blue b^2 & = 13 + 12\sqrt 2 & \small \blue{\text{Note that }b^2 + b^2 = (a-1)^2} \\ a^2 + \frac {4a\blue{(a-1)}}\blue{\sqrt 2} + \frac {2\blue{(a-1)^2}}\blue 2 & = 13 + 12\sqrt 2 & \small \blue{\implies b = \frac {a-1}{\sqrt 2}} \\ \left(2+2\sqrt 2\right)a^2 - \left(2+2\sqrt 2\right)a + 1 & = 13 + 12 \sqrt 2 \\ a^2 - a - 6 & = 0 \\ (a-3)(a+2) & = 0 & \small \blue{\text{Since }a>0} \\ \implies a & = 3 \end{aligned}$

By Pythagorean theorem ,

$\begin{aligned} r^2 & = \left(\frac a2 + b \right)^2 + \left(\frac a2\right)^2 \\ & = \left(\frac a2 + \frac {a-1}{\sqrt 2} \right)^2 + \left(\frac a2\right)^2 \\ & = \left(\frac 32 + \sqrt 2 \right)^2 + \frac 94 \\ & = \frac 94 + 3\sqrt 2 + 2 + \frac 94 \\ & = \frac {13+6\sqrt 2}2 \\ \implies A & = \frac {13+6\sqrt 2}2 \pi = \frac {169-72}{2(13-6\sqrt 2)} \pi = \frac {97}{26-12\sqrt 2} \pi \end{aligned}$

Therefore $\alpha + \beta + \lambda + \omega = 97 + 26 + 12 + 2 = \boxed{137}$ .