It's All Areas!
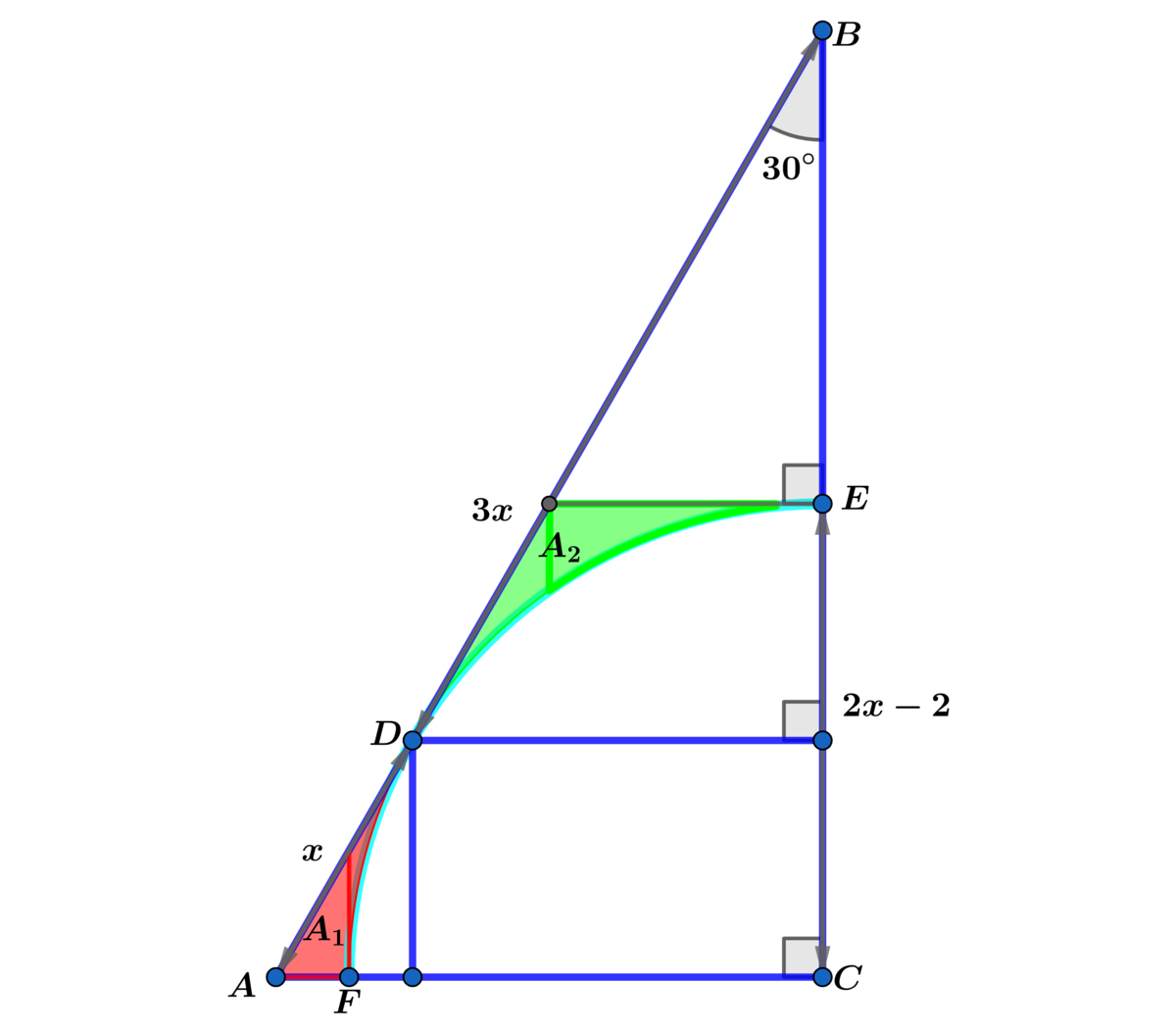
In right △ A B C , m ∠ A B C = 3 0 ∘ , A D = x , D B = 3 x and the quarter of the circle has radius C E = 2 x − 2 .
If the sum of the areas A 1 + A 2 = a ( b + c a − ( d + e a ) π ) , where a , b , c , d and e are coprime positive integer, find a + b + c + d + e .
The answer is 52.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Interestingly, H E = A D .
I found the same answer, however, I was a little bit confused by the sentence "coprime positive integers" because a and b, or b and e are not coprime integers each other.
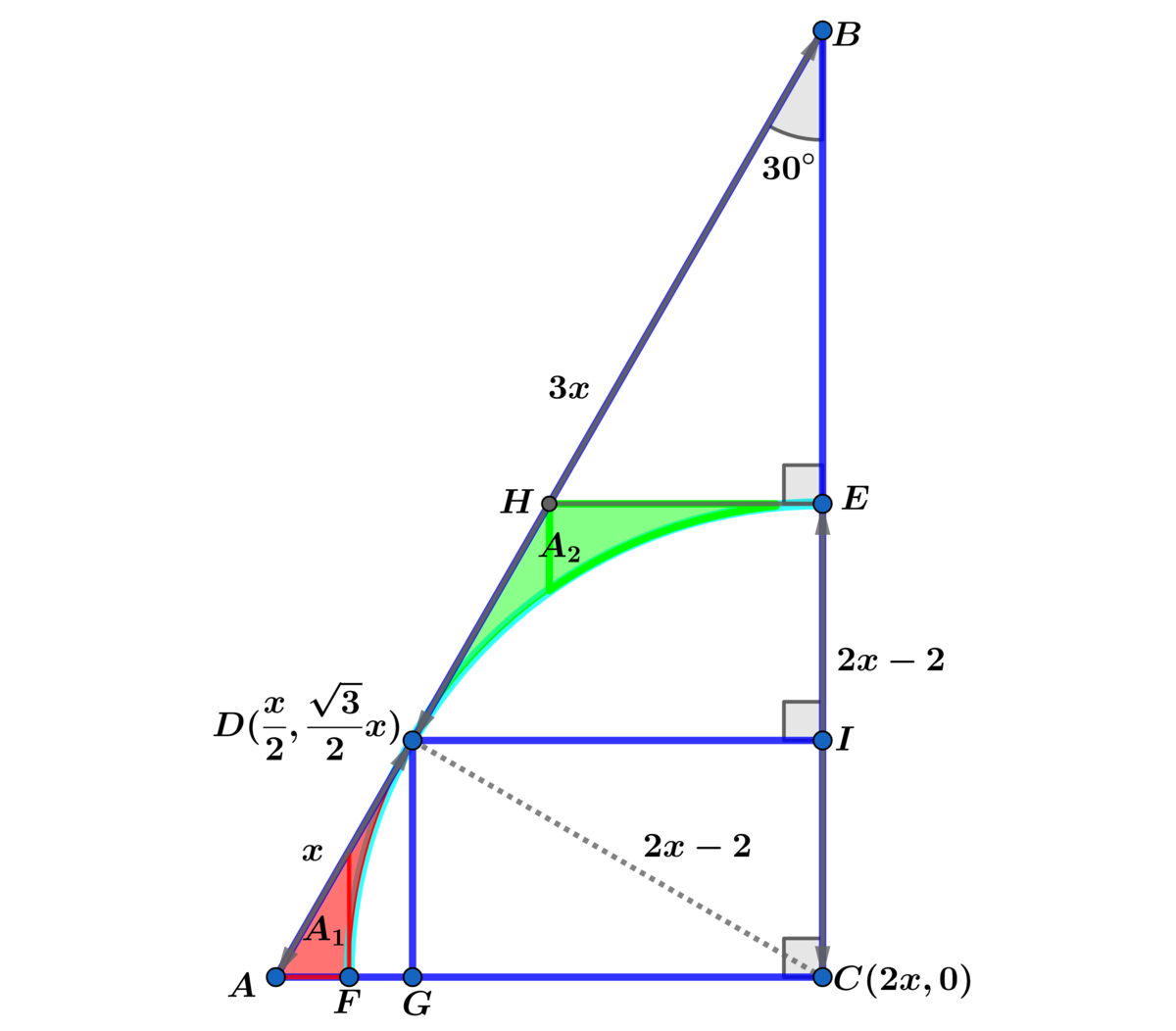
A F = 2 x − ( 2 x − 2 ) = 2 , G D = 2 3 x , A G = 2 x ⟹
( C D ) 2 = 4 ( x − 1 ) 2 = 1 6 x 2 − 3 2 x + 1 6 = ( 2 x − 2 x ) 2 + 4 3 x 2 = 1 2 x 2 ⟹ x 2 − 8 x + 4 = 0 ⟹ x = 4 ± 2 3
x = 4 − 2 3 ⟹ 2 ( x − 1 ) = 2 ( 3 − 2 3 ) < 0 ∴ choose x = 4 + 2 3
⟹ radius r = 2 x − 2 = 2 ( 3 + 2 3 )
For A 2 :
Let θ = m ∠ D C E
⟹ tan ( θ ) = 3 ⟹ θ = 3 π ⟹ A s e c t o r C D E = 2 1 θ r 2 = 2 1 ( 3 π ) ( 4 ) ( 3 + 2 3 ) 2 =
2 π ( 7 + 4 3 )
and A △ C D I = 2 1 ( 2 3 x ) ( 2 3 x ) = 8 3 3 x 2 = 8 3 3 ( 4 + 2 3 ) 2 = 2 3 3 ( 7 + 4 3 )
Let R 2 be region D E I ⟹ A R 2 = A s e c t o r C D E − A △ C D I = 2 ( 7 + 4 3 ) ( 4 π − 3 3 )
B C = 2 3 x ⟹ B E = 2 3 x − ( 2 x − 2 ) = 2 ( ( 3 − 1 ) x + 1 ) =
2 ( 2 3 + 3 ) and △ A D G ∼ △ H B E ⟹ 3 1 = 2 ( 2 3 + 3 ) H E ⟹ H E = 3 4 3 + 6 = 4 + 2 3 = x and D I = 2 3 x = 3 ( 2 + 3 ) and I E = C E − C I =
( 2 4 − 3 ) x − 2 = 3 + 2 3 ⟹ area of trapezoid
A D H E I = 2 1 ( 5 ) ( 2 + 3 ) ( 3 + 2 3 ) = 2 5 ( 1 2 + 7 3 )
⟹ A 2 = A D H E I − A R 2 = 4 8 + 2 8 3 − ( 1 4 + 8 3 ) π
For A 1 :
m ∠ F C D = 6 π ⟹ A s e c t o r C D F = 2 1 ( 6 π ) ( 4 ) ( 3 + 2 3 ) 2 = π ( 7 + 4 3 )
and A △ D G C = 2 3 3 ( 7 + 4 3 )
Let R 1 be region F D G ⟹ A R 1 = A s e c t o r C D F − A △ D G C = 2 ( 7 + 4 3 ) ( 2 π − 3 3 )
and A △ A D G = 8 3 x 2 = 2 3 ( 7 + 4 3 )
⟹ A 1 = A △ A D G − A R 1 = ( 7 + 4 3 ) ( 2 3 − π ) = 2 4 + 1 4 3 − ( 7 + 4 3 ) π
⟹ A 1 + A 2 = 7 2 + 4 2 3 − ( 2 1 + 1 2 3 ) π = 3 ( 2 4 + 1 4 3 − ( 7 + 4 3 ) π ) =
a ( b + c a − ( d + e a ) π ) ⟹ a + b + c + d + e = 5 2 .
I found the same answer, however, I was a little bit confused by the sentence "coprime positive integers" because a and b, or b and e are not coprime integers each other.
Log in to reply
Coprime means the greatest common factor of all the integers is 1. Which is the case in this problem. Your thinking of pairwise positive integers.
Let the point to the left of E be H , and let B E = y .
Since ∠ A B C = 3 0 ° and A B = 4 x , from △ A B C we have A C = 2 x and B C = 2 3 x = 2 x − 2 + y .
By the tangent-secant theorem , ( 3 x ) 2 = y ( 4 x − 4 + y ) .
These two equations solve to x = 4 + 2 3 and y = 6 + 4 3 .
That means A C = 2 x = 2 ( 4 + 2 3 ) = 8 + 4 3 and E C = 2 x − 2 = 2 ( 4 + 2 3 ) − 2 = 6 + 4 3 .
Since ∠ H B E = 3 0 ° and B E = y = 6 + 4 3 , from △ H B E we have H E = 3 3 ( 6 + 4 3 ) = 4 + 2 3 .
The sum of the areas A 1 + A 2 is the difference between the areas of trapezoid A H E C and the quarter circle, so:
A 1 + A 2 = 2 1 ( A C + H E ) ⋅ E C − 4 1 π ⋅ E C 2
A 1 + A 2 = 2 1 ( 8 + 4 3 + 4 + 2 3 ) ⋅ ( 6 + 4 3 ) − 4 1 π ⋅ ( 6 + 4 3 ) 2
A 1 + A 2 = 3 ( 2 4 + 1 4 3 − ( 7 + 4 3 ) π ) .
Therefore, a = 3 , b = 2 4 , c = 1 4 , d = 7 , e = 4 , and a + b + c + d + e = 5 2 .