It's All Areas
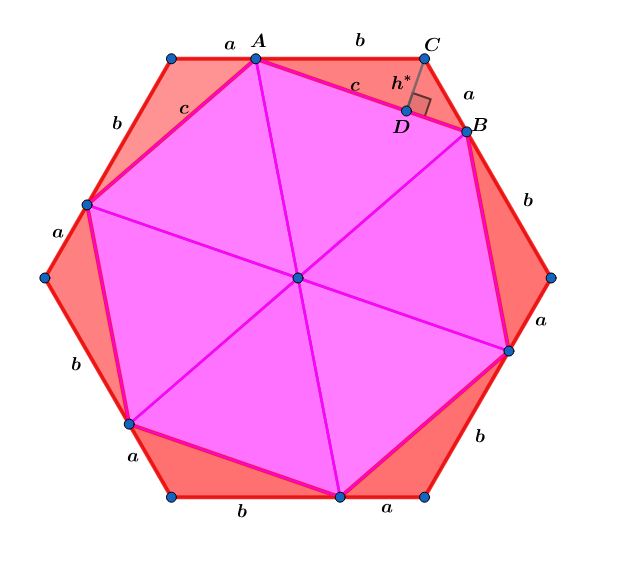
Let the diagram above be extended to a regular n -gon and A j , where ( 1 ≤ j ≤ n ) , be the area of one of the red triangles.
If n → ∞ lim j = 1 ∑ n A j = π ( a 2 + 2 a b − 1 2 b 2 ) , find b a .
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
In the triangle A B C , ∠ C = n n − 2 π = π − n 2 π .
The area of one of the red triangles is therefore A j = 2 1 a b sin C = 2 1 a b sin ( π − n 2 π ) = 2 1 a b sin n 2 π
There are n of these triangles; so the sum of their areas is 2 n a b sin n 2 π
Since sin θ ≈ θ for small θ , in the limit this becomes simply π a b
(which is interesting - I wonder how this is related to the area of an ellipse?)
Equating this to the given form, and letting x = b a , π a b x x 2 + x − 1 2 = π ( a 2 + 2 a b − 1 2 b 2 ) = x 2 + 2 x − 1 2 = 0
whose unique positive root is x = 3 .
Let m ( ∠ A C B ) = n ( n − 2 ) 1 8 0 be one of the interior angles of the larger n − g o n .
sin ( n ( n − 2 ) 1 8 0 ) = sin ( 1 8 0 − n 3 6 0 ) = sin ( n 3 6 0 ) = sin ( n 2 π ) .
Using the law of sines ⟹ sin ( n 2 π ) c = sin ( α ) a ⟹ sin ( α ) = c a sin ( n 2 π ) ⟹ h ∗ = c a b sin ( n 2 π ) ⟹ ∑ j = 1 n A j = n 2 1 ( c ) ( c a b sin ( n 2 π ) ) = 2 n a b sin ( n 2 π ) .
Using the inequality cos ( x ) < x sin ( x ) < 1 ⟹ π cos ( n π ) < 2 n sin ( n 2 π ) < π ⟹ lim n → ∞ ∑ j = 1 n A j = π a b ⟹ ∑ j = 1 n A j converges to the area of an ellipse.
lim n → ∞ ∑ j = 1 n A j = π a b = π ( a 2 + 2 a b − 1 2 b 2 ) ⟹ a 2 + a b − 1 2 b 2 = 0 ⟹ ( a − 3 b ) ( a + 4 b ) = 0 since a , b > 0 ⟹ b a = 3 .