It's All Circles!
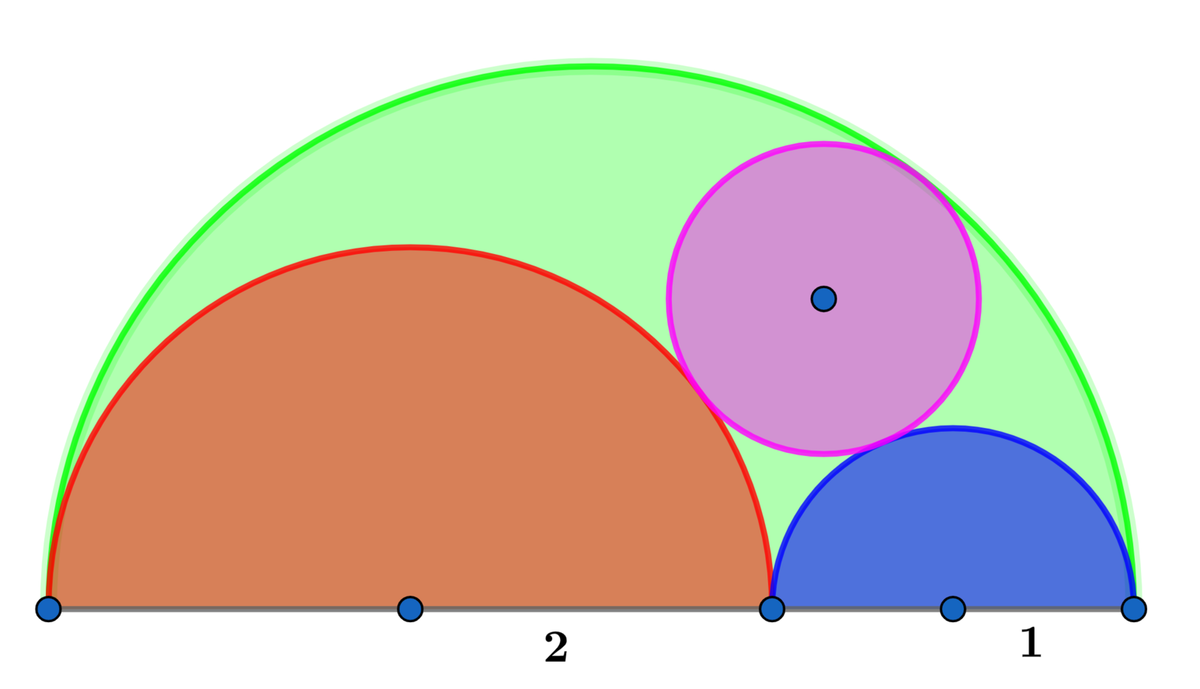
The red and the blue semicircles have radii of 2 and 1 respectively and the purple circle is tangent to the red and blue semicircles and the large semicircle.
If the area of the green region A = b a π , where a and b are coprime positive integers, find a + b .
The answer is 111.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Let the center of the large green semicircle be the origin ( 0 , 0 ) , then the center of the red semicircle is ( − 1 , 0 ) and the center of the blue semicircle is ( 2 , 0 ) . Let the center of the purple circle be ( x , y ) and its radius be r . Then we have:
⎩ ⎪ ⎨ ⎪ ⎧ ( x + 1 ) 2 + y 2 = ( 2 + r ) 2 ( x − 2 ) 2 + y 2 = ( 1 + r ) 2 x 2 + y 2 = ( 3 − r ) 2 . . . ( 1 ) . . . ( 2 ) . . . ( 3 )
From ( 1 ) − ( 2 ) : 6 x − 3 = 2 r + 3 ⟹ 6 x = 2 r + 6 . . . ( 4 ) .
From ( 1 ) − ( 3 ) : 2 x + 1 = 1 0 r − 5 ⟹ 2 x = 1 0 r − 6 . . . ( 5 ) .
From 3 × ( 5 ) − ( 4 ) : 0 = 2 8 r − 2 4 ⟹ r = 7 6 .
Therefore the area of green region A = π ( 2 3 2 − 2 2 2 − 2 1 2 − ( 7 6 ) 2 ) = 4 9 6 2 π . ⟹ a + b = 6 2 + 4 9 = 1 1 1 .
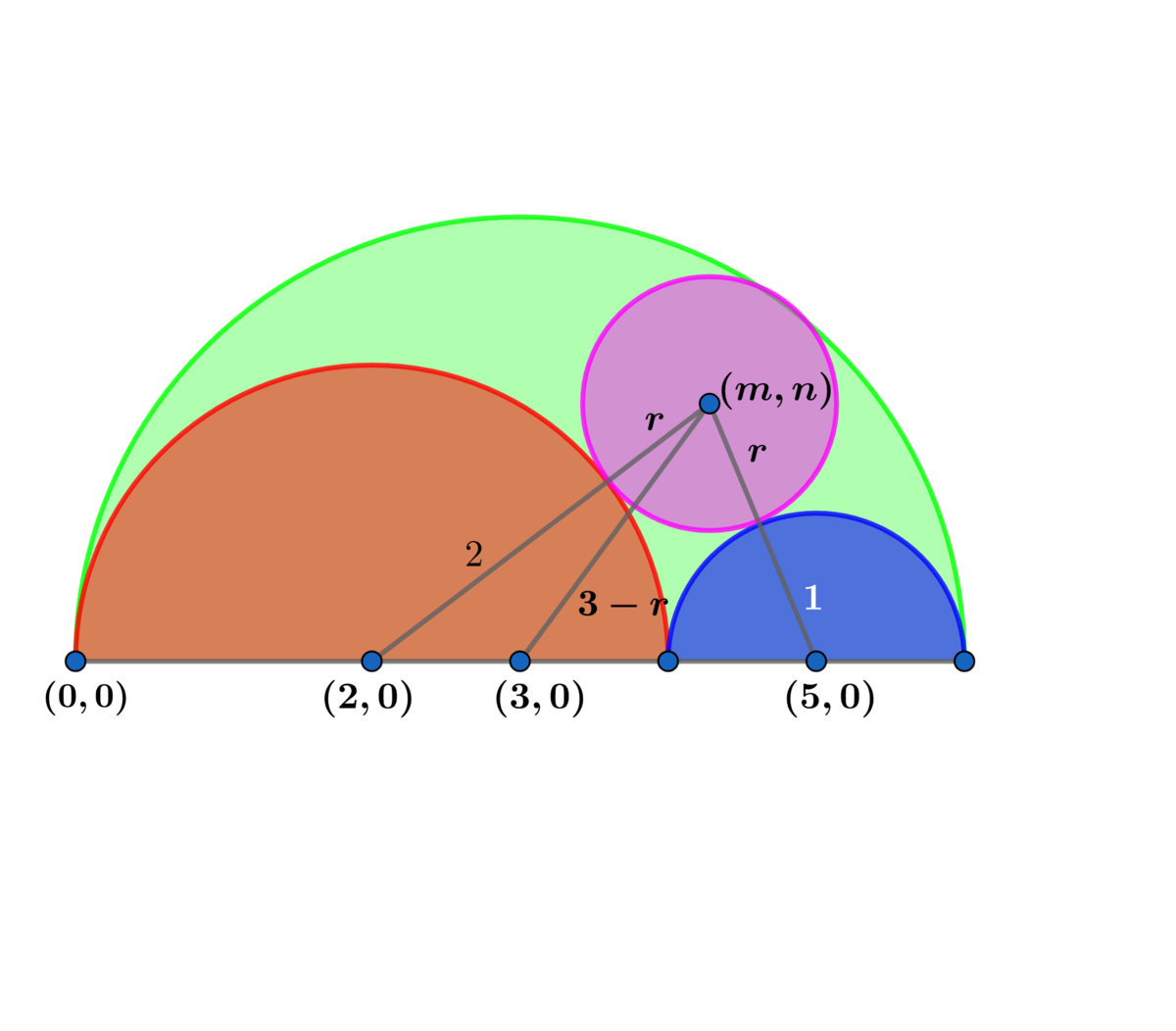
Let ( m , n ) be center of the purple circle with radius r .
( 1 ) : ( m − 2 ) 2 + n 2 = ( 2 + r ) 2 ⟹ m 2 − 4 m + 4 + n 2 = 4 + 4 r + r 2
( 2 ) : ( m − 5 ) 3 + n 2 = ( 1 + r ) 2 ⟹ m 2 − 1 0 m + 2 5 + n 2 = 1 + 2 r + r 2
( 3 ) : ( m − 3 ) 2 + n 2 = ( 3 − r ) 2 ⟹ m 2 − 6 m + 9 + n 2 = 9 − 6 r + r 2
Subtracting 2 ) from ( 1 ) we obtain 3 m − r = 1 2
Subtracting ( 3 ) from ( 1 ) we obtain m = 5 r
⟹ 1 4 r = 1 2 ⟹ r = 7 6
⟹ A = ( 2 9 − ( 2 + 2 1 + 4 9 3 6 ) ) π = ( 2 − 4 9 3 6 ) π = 4 9 6 2 π = b a π ⟹ a = b = 1 1 1 .
Label the diagram as follows, where C is the center of the large semi-circle:
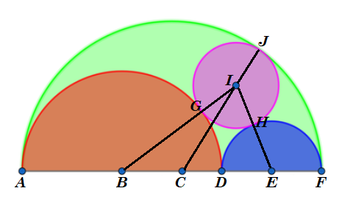
The large semi-circle has a radius of A C = C F = C J = 2 1 A F = 2 1 ( A B + B D + D E + E F ) = 2 1 ( 2 + 2 + 1 + 1 ) = 3 which means C E = C F − E F = 3 − 1 = 2 . Also, B E = B D + D E = 2 + 1 = 3 .
Let r = I G = I H = I J . Then C I = C J − I J = 3 − r , B I = B G + I G = 2 + r , and E I = E H + I H = 1 + r .
By the law of cosines on △ B E I and △ C E I , cos ∠ I E C = 2 ⋅ 3 ⋅ ( r + 1 ) 3 2 + ( r + 1 ) 2 − ( r + 2 ) 2 = 2 ⋅ 2 ⋅ ( r + 1 ) 2 2 + ( r + 1 ) 2 − ( 3 − r ) 2 , which solves to r = 7 6 .
The area of the green region is then the area of the large semi-circle minus the sum of the areas of the two smaller semi-circles and the circle, which is A = 2 3 2 π − ( 2 2 2 π + 2 1 2 π + 7 2 6 2 π ) = 4 9 6 2 π .
Therefore, a = 6 2 , b = 4 9 , and a + b = 1 1 1 .
Descartes' circle theorem is the key here.
Let the radius of the orange and the blue semicircles are r 1 = 2 , r 2 = 1 , and let R = r 1 + r 2 = 3 denote the radius of the green semicircle.
Denote the curvature of the pink circle as k 3 .
The curvatures of the blue, orange and green semicircles are k 1 = 1 , k 2 = 2 1 , k 4 = − 3 1 .
Using Descartes' circle theorem, we get ( 1 + 2 1 + k 3 − 3 1 ) 2 = 2 ( 1 2 + ( 2 1 ) 2 + k 3 2 + ( − 3 1 ) 2 )
Solving the equation above gives k 3 = 6 7 , so the radius of the pink circle is 7 6 .
The area of the green shaded region is 2 1 π ⋅ 3 2 − 2 1 π ⋅ 2 2 − 2 1 π ⋅ 1 2 − π ⋅ ( 7 6 ) 2 = 4 9 6 2 π
The answer is 6 2 + 4 9 = 1 1 1 .