It's All Geometry!
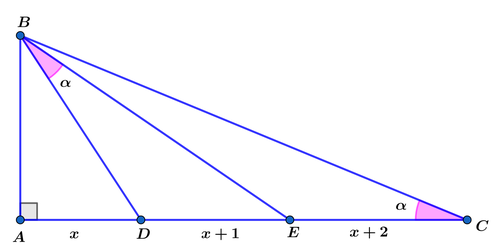
In right △ A B C above, A D = x , D E = x + 1 , E C = x + 2 and m ∠ D B E = m ∠ B C A = α . Find the value of x for which the area A △ D B E = x 2 − 1 .
The answer is 4.254994.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
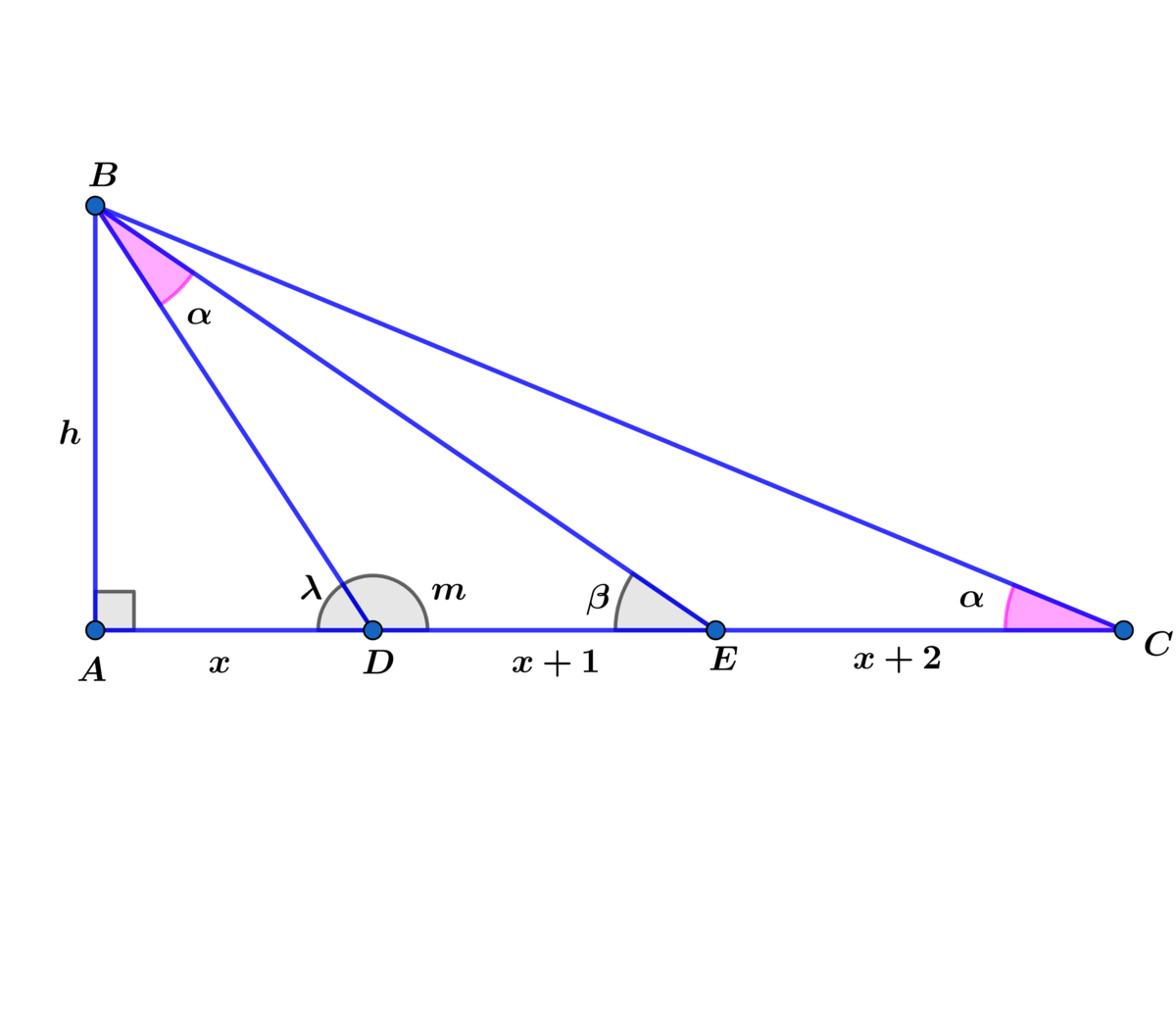
m = 1 8 0 − ( α + β ) = 1 8 0 − λ ⟹ λ = α + β
⟹ tan ( λ ) = x h = tan ( α + β ) , where tan ( β ) = 2 x + 1 h and tan ( α ) = 3 x + 3 h
⟹ x h = tan ( α + β ) = 1 − tan ( α ) tan ( β ) tan ( α ) + tan ( β ) = 1 − ( 3 x + 3 ) ( 2 x + 1 ) h 2 3 x + 3 h + 2 x + 1 h = ( 6 x 2 + 9 x + 3 − h 2 5 x + 4 ) h
⟹ x 1 = 6 x 2 + 9 x + 3 − h 2 5 x + 4 ⟹ 6 x 2 + 9 x + 3 − h 2 = 5 x 2 + 4 x
⟹ h 2 = x 2 + 5 x + 3 ⟹ h = x 2 + 5 x + 3
⟹ A △ D B E = 2 1 ( x + 1 ) ( x 2 + 5 x + 3 ) = x 2 − 1 = ( x − 1 ) ( x + 1 ) ⟹
x 2 + 5 x + 3 = 2 ( x − 1 ) ⟹ x 2 + 5 x + 3 = 4 x 2 − 8 x + 4 ⟹
3 x 2 − 1 3 x + 1 = 0 ⟹ x = 6 1 3 ± 1 5 7 and x > 1 ⟹ x = 6 1 3 + 1 5 7 ≈ 4 . 2 5 4 9 9 4 .
You don't need the constraint x > 1 because if we are given that the area is x 2 − 1 , then x > 1 follows.
Log in to reply
I did realize that since A △ D B E = x 2 − 1 ⟹ x > 1 , but I added it. I removed it.
Since A △ D B A = x 2 − 1 , ⟹ A B = 2 ( x − 1 ) so that A △ D B A = 2 1 A B ⋅ D E = 2 1 ⋅ 2 ( x − 1 ) ( x + 1 ) = x 2 − 1 . The B D = A B 2 + A D 2 = ( 2 ( x − 1 ) ) 2 + x 2 = 5 x 2 − 8 x + 4 . Note that △ B D E and △ B C D are similar, then we have:
D E B D x + 1 5 x 2 − 8 x + 4 5 x 2 − 8 x + 4 3 x 2 − 1 3 x + 1 ⟹ x = B D C D = 5 x 2 − 8 x + 4 2 x + 3 = 2 x 2 + 5 x + 3 = 0 = ⎩ ⎪ ⎨ ⎪ ⎧ 6 1 3 + 1 5 7 ≈ 4 . 2 5 4 9 9 4 0 1 4 6 1 3 − 1 5 7 ≈ 0 . 0 7 8 3 3 9 3 1 9
From A △ D B E = x 2 − 1 ⟹ x > 1 , therefore x ≈ 4 . 2 5 .
The area of Δ D B E is 2 1 D E ⋅ A B .
Since D E = x + 1 , this means that A B = 2 x − 2 .
From Δ A B C , tan α = 3 x + 3 2 x − 2
From triangles Δ A B D and Δ A B E , α = tan − 1 2 x − 2 2 x + 1 − tan − 1 2 x − 2 x
Using the tangent addition formula, and after a bit of paperwork, this becomes tan α = 6 x 2 − 7 x + 4 2 x 2 − 2
Combining these results and tidying, we get the cubic ( x − 1 ) ( 3 x 2 − 1 3 x + 1 ) = 0
The only root that makes sense in the context of the problem is x = 6 1 3 + 1 5 7 ≈ 4 . 2 5 5