It's All Geometry!
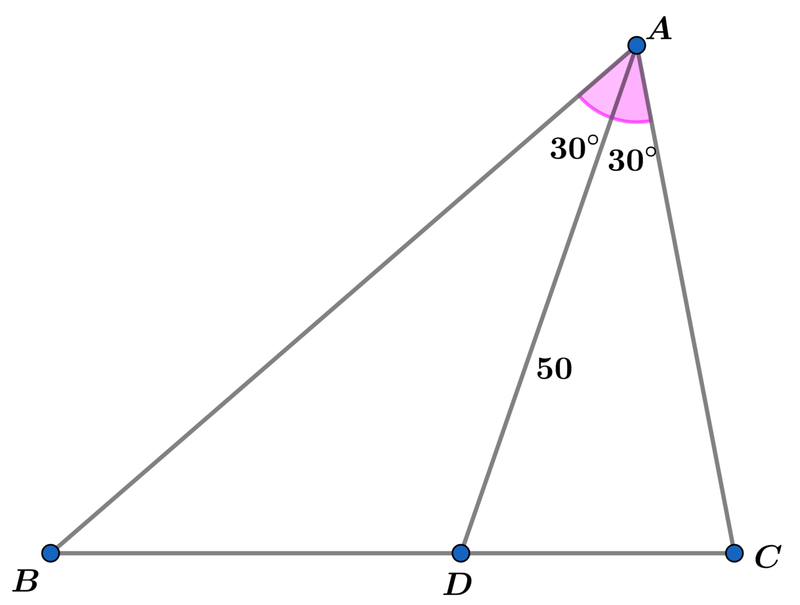
In △ A B C , A B = 2 3 A C , m ∠ B A D = m ∠ D A C = 3 0 ∘ , and A D = 5 0 . If the area of △ A B C , A △ A B C = c b b a c b , where a , b , and c are prime numbers, find a + b + c .
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
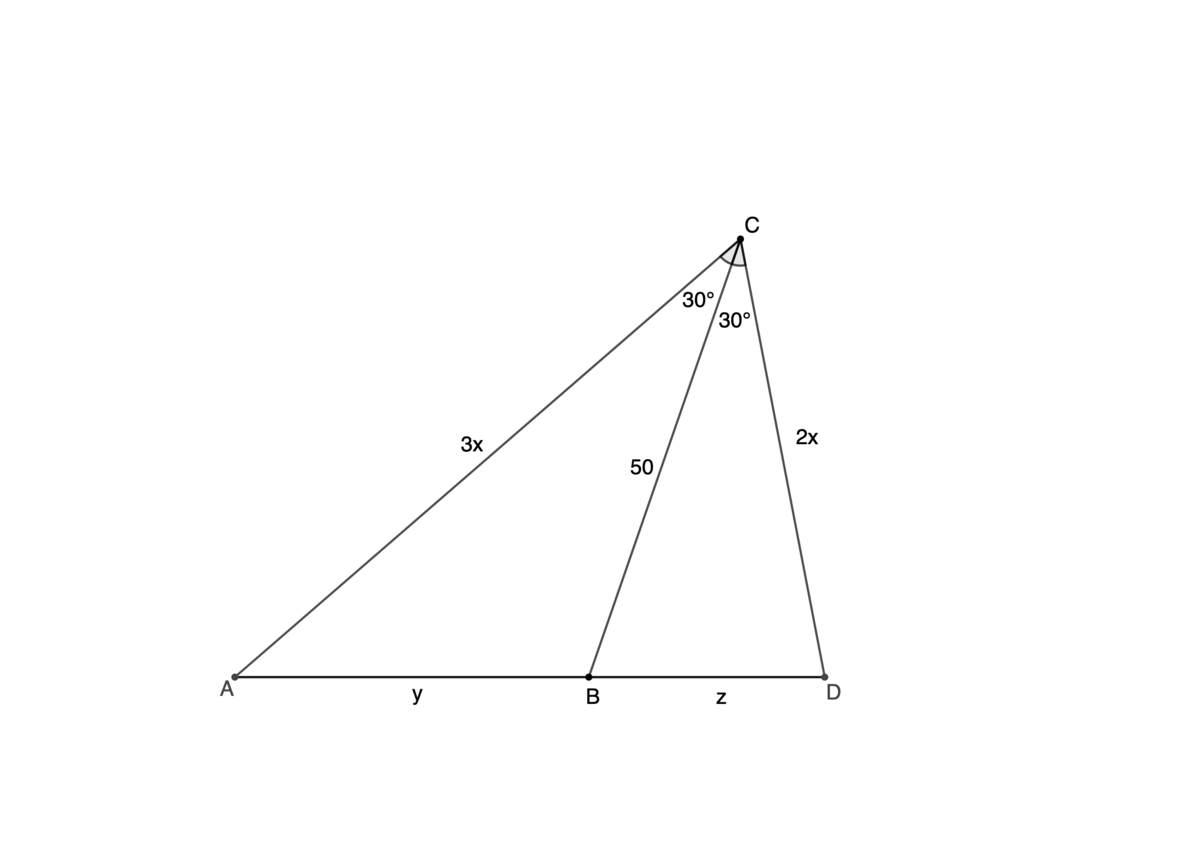
Using the cosine rule on the three triangles:
( 3 x ) 2 + 5 0 2 − y 2 = 2 ⋅ 3 x ⋅ 5 0 ⋅ cos 6 π
( 2 x ) 2 + 5 0 2 − z 2 = 2 ⋅ 2 x ⋅ 5 0 ⋅ cos 6 π
( 3 x ) 2 + ( 2 x ) 2 − ( y + z ) 2 = 2 ⋅ 3 x ⋅ 2 x ⋅ cos 3 π
Three equations three unkowns, solve for the sides and compute the area with heron's formula (see below):
△ A C D = 1 8 1 5 6 2 5 3 = 3 ⋅ 2 3 5 3 ⋅ 2 ⟹ a = 5 , b = 3 , c = 2 ⟹ a + b + c = 1 0
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
|
1 |
|
blah 1 8 1 5 6 2 5 3 = 3 ⋅ 2 3 5 3 ⋅ 2
Similar solution as @Rocco Dalto's
By sine rule ,
⎩ ⎪ ⎨ ⎪ ⎧ A D A B = sin B sin ∠ A D B = sin B sin ( 1 8 0 ∘ − ∠ A D B = sin B sin ∠ A D C A D A C = sin C sin ∠ A D C . . . ( 1 ) . . . ( 2 )
From ( 2 ) ( 1 ) :
A C A B 2 3 3 sin B ⟹ tan B = sin B sin C = sin B sin ( 1 2 0 ∘ − B ) = 2 sin ( 1 2 0 ∘ − B ) = 3 cos B + sin B = 2 3 Note that C = 1 8 0 ∘ − 6 0 ∘ − B
From ( 1 ) :
A D A B 5 0 A B 2 5 A B ⟹ A B = sin B sin ∠ A D C = sin B sin ( B + 3 0 ∘ ) = sin B 2 1 cos B + 2 3 sin B = cot B + 3 = 3 2 + 3 = 3 5 3 Note that ∠ A D C = B + 3 0 ∘
The area of △ A B C : A △ A B C = 2 A B ⋅ A C sin 6 0 ∘ = 2 3 2 A B 2 ⋅ 2 3 = ( 3 5 3 ) 2 ⋅ 2 3 1 = 6 3 5 6 . Therefore a + b + c = 5 + 2 + 3 = 1 0
Let A C = 2 x ⟹ A B = 3 x and α + λ = 1 2 0 ∘ ⟹ α = 1 2 0 ∘ − λ .
Using the law of cosines on △ A B C with included ∠ B A C ⟹ y = 7 x .
Using the law of sines on △ A B C ⟹ sin ( λ ) 3 x = sin ( 6 0 ∘ ) 7 x = 3 2 7 x ⟹
sin ( λ ) = 2 3 7 3
Using the law of sines on △ D A C ⟹ sin ( λ ) 5 0 = sin ( 3 0 ∘ ) n = 2 n ⟹
n = sin ( λ ) 2 5 = 3 5 0 3 7
Similarly using the law of sines on △ B A D ⟹ m = sin ( α ) 2 5 = sin ( 1 2 0 ∘ − λ ) 2 5 =
3 cos ( λ ) + sin ( λ ) 5 0 = 2 5 3 7 , where cos ( λ ) = 2 7 1
⟹ y = m + n = 3 1 2 5 3 7 = 7 x ⟹ x = 3 3 1 2 5 ⟹ 2 x = 3 3 2 5 0 ⟹
h = 2 x sin ( λ ) = 7 1 2 5 ⟹ A △ A B C = 2 1 y h = 2 ∗ 3 3 1 2 5 2 = 2 ∗ 3 3 5 ( 2 ∗ 3 ) =
c ∗ b b a c ∗ b ⟹ a + b + c = 1 0 .