Its all in the basics
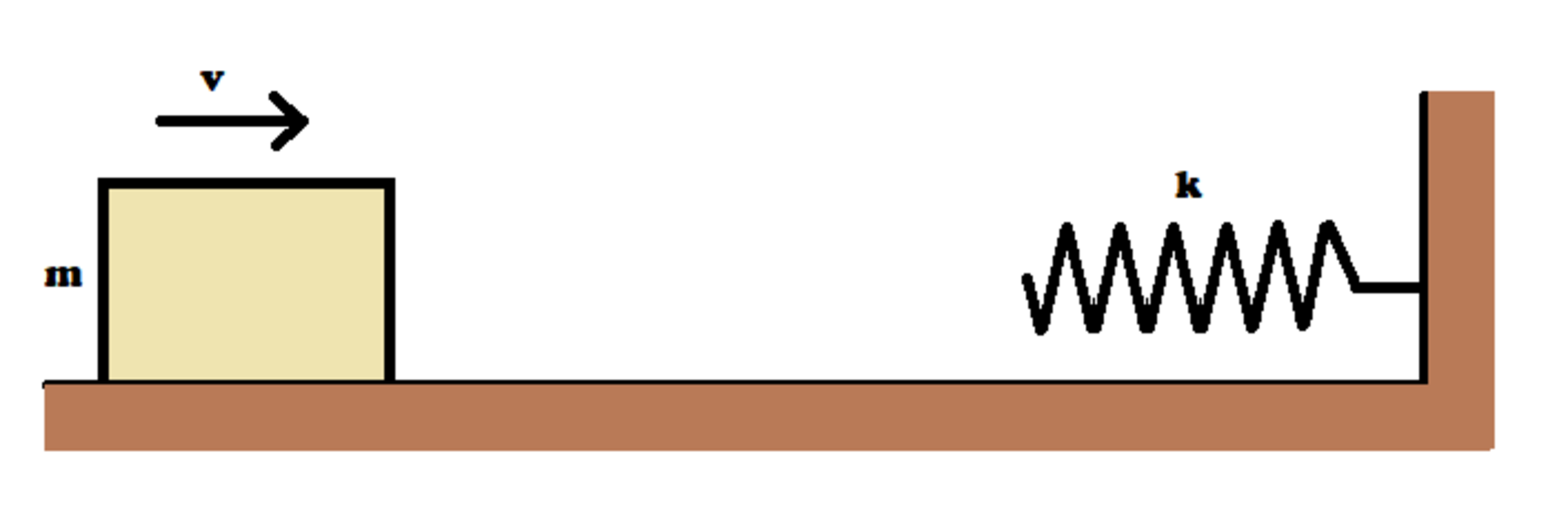
A block of mass sliding on a smooth horizontal surface with a velocity meets a long horizontal spring fixed at one end having a spring constant . Find the maximum compression of the spring. Will the velocity of the block be same as when it comes back to the original position?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
According to the work energy theorem : 2 1 m ⋅ ( v ) 2 = 2 1 k ⋅ x 2 where, k is the spring constant and x is the maximum compression in the spring. v is the initial velocity of the block. At maximum compression state the velocity of the block becomes zero . So, on solving the above for x we will get : x = v k m Coming, to the next part of the question, as the surface is friction-less you may think that the block will reach with same velocity. It is true, but the thing you should consider is that, only the magnitude of velocity is same whereas the direction is opposite . So, the block will return with − v velocity which is not same as v .