Inscribed Circles
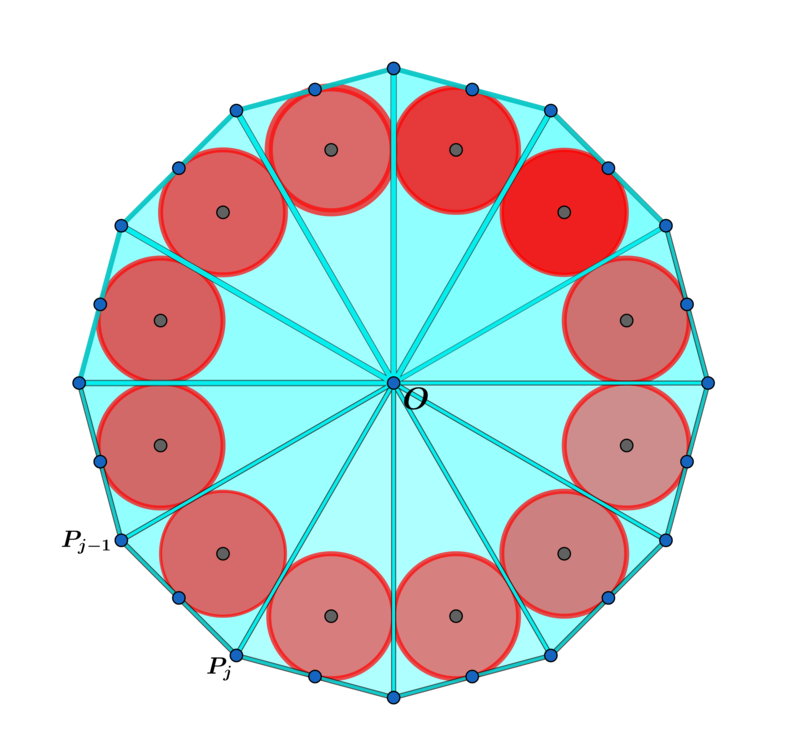
Extend the dodecagon to a regular n -gon. Let n ≥ 4 be a positive integer and 1 ≤ j ≤ n . A circle is inscribed in each congruent isosceles triangle P j − 1 O P j as shown above. Let C j ( n ) be the area of each congruent circle and T j ( n ) be the area of each congruent isosceles triangle P j − 1 O P j .
Let A ( n ) = j = 1 ∑ n C j ( n ) . For fixed j , find n → ∞ lim T j ( n ) A ( n ) to eight decimal places.
The answer is 9.86960440.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
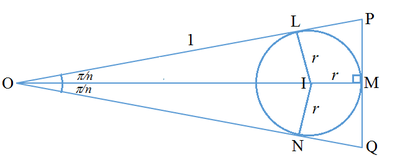
A regular n -gon is formed from n congruent central isosceles triangles where n 2 π is the measure of the angle between the equal sides. Let the side length of the equal sides be 1, then the area of the central isosceles triangle, A △ = 2 1 sin n 2 π .
Let M be the midpoint of the base of the central isosceles triangle P Q ; then ∠ P O M = ∠ Q O M = n π . Let also the center of the circle inscribed in the central isosceles triangle be I and its radius be r , and the altitudes from I to O P and O Q be I L and I N respectively. Then we have:
O M A O cos n π cos n π = O I + I M = sin n π I L + I M = sin n π r + r Note that A O = 1 and I L = I M = r
⟹ r = sin n π 1 + 1 cos n π = 2 ( 1 + sin n π ) sin n 2 π
Then the area of the incircle is A ◯ = 4 ( 1 + sin n π ) 2 π sin 2 n 2 π and the required limit:
n → ∞ lim A △ n A ◯ = n → ∞ lim 4 ( 1 + sin n π ) 2 n π sin 2 n 2 π × sin n 2 π 2 = n → ∞ lim 2 ( 1 + sin n π ) 2 n π sin n 2 π = n → ∞ lim n 2 π π 2 sin n 2 π × n → ∞ lim ( 1 + sin n π ) 2 1 = π 2 ≈ 9 . 8 6 9 6 0 4 4 0
Let O P j = 1
Notice that n → ∞ lim n T j ( n ) = π (equal to a unit circle)
And A j ( n ) = r I 2 π , r I is the inradius of △ O P j P j − 1
So r I = 2 T j ( n ) O P j + O P j − 1 + P j P j − 1 = 2 + P j P j − 1 2 T j ( n )
n → ∞ lim T j ( n ) A ( n )
= n → ∞ lim T j ( n ) n A j ( n )
= n → ∞ lim n T j ( n ) n 2 A j ( n )
= n → ∞ lim π n 2 A j ( n )
= n → ∞ lim π n 2 r I 2 π
= n → ∞ lim ( n r I ) 2
= n → ∞ lim ( 2 + P j P j − 1 n 2 T j ( n ) ) 2
= n → ∞ lim ( 2 + 0 n 2 T j ( n ) ) 2
= n → ∞ lim ( n T j ( n ) ) 2
= π 2
n → ∞ lim 2 1 sin ( n 2 π ) π n ( 2 ( sin ( n π ) + 1 ) sin ( n 2 π ) ) 2 ⟹ π 2
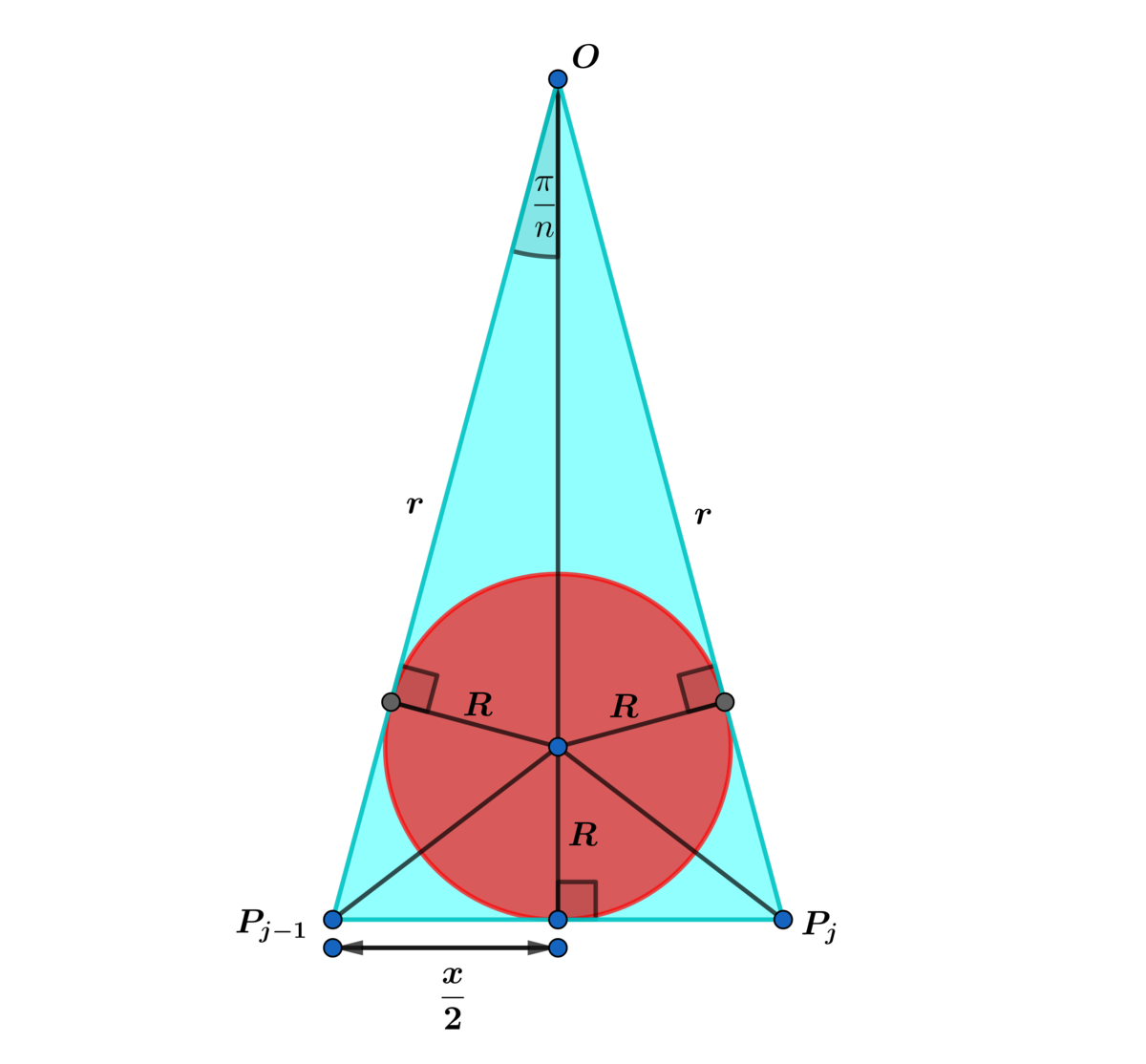
2 x = r sin ( n π ) ⟹ h = r cos ( n π ) ⟹ T j ( n ) = 2 1 sin ( n 2 π ) r 2 for each triangle P j − 1 O P j .
and,
T j ( n ) = r R + 2 1 x R = 2 R ( 2 r + x ) ⟹ R = 2 r + x 2 T j ( n ) = 2 r + 2 r sin ( n π ) ) sin ( n 2 π ) r 2 = 2 ( 1 + sin ( n π ) ) sin ( n 2 π ) r
⟹ C j ( n ) = 4 ( 1 + sin ( n π ) ) 2 π sin 2 ( n 2 π ) r 2
⟹ A ( n ) = ( 1 + sin ( n π ) ) 2 2 π ( 2 n sin 2 ( n 2 π ) r 2 )
and,
For fixed j we have: T j ( n ) A ( n ) = ( 1 + sin ( n π ) ) 2 π ( 2 n sin ( n 2 π ) ) .
lim n → ∞ ( 1 + sin ( n π ) ) 2 = 1
and,
For π lim n → ∞ 2 n sin ( n 2 π ) :
Using the inequality: cos ( x ) < x sin ( x ) < 1 ⟹ cos ( n 2 π ) < n 2 π sin ( n 2 π ) < 1 ⟹ π cos ( n 2 π ) < 2 n sin ( n 2 π ) < π
and π lim n → ∞ cos ( n 2 π ) = π ⟹ π lim n → ∞ 2 n sin ( n 2 π ) = π ∗ π = π 2
⟹ lim n → ∞ T j ( n ) A ( n ) = π 2 ≈ 9 . 8 6 9 6 0 4 4 0 .
Let's make the height of the triangles (based on the sides of the n -gon) equal to 1 for simplicity. Then the sides of the n -gon are 2 tan ( n π ) and the area of the triangles is tan ( n π ) . Consider a right triangle with its hypotenuse connecting the center of a circle to an adjacent vertex of the n -gon to see that the radius of the circles is tan ( n π ) tan ( 4 π − 2 n π ) .The limit we seek is n → ∞ lim tan ( n π ) n π tan 2 ( n π ) tan 2 ( 4 π − 2 n π ) = π n → ∞ lim n tan ( n π ) = π 2 ≈ 9 . 8 6 9 6 0 4 4 0