it's only lines and circles
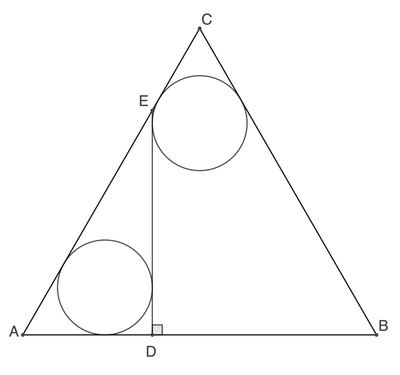
△ A B C is equilateral with unit side length. Two congruent circles are tangent to the triangle sides as well as the perpendicular D E . If the length of A D can be expressed as c a + b , where a , b , and c are integers with a being square-free, submit a + b + c .
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Fletcher Mattox , you can use \dfrac 12 for 2 1 instead of using \displaystyle in front. Similarly, \dbinom mn for ( n m ) .
Log in to reply
Thank you for taking time to improve my formatting. I value that.
Let the radius of each circle be r . Then
r ( 3 + 1 + 1 ) = 2 1 (since the length of each side of the triangle is 1 )
⟹ r = 4 + 2 3 1 = ( 3 + 1 ) 2 1
So,
∣ A D ∣ = r ( 3 + 1 ) = 3 + 1 1
= 2 3 − 1
Hence, a = 3 , b = − 1 , c = 2 and
a + b + c = 3 − 1 + 2 = 4 .
Let the radius of the circles be r . Then we note that the center of the top circle is on the median of equilateral △ A B C . Therefore we have:
tan 3 0 ∘ r + r + r 3 r + 2 r ⟹ r A D = 2 1 = 2 1 = 2 ( 2 + 3 1 = 2 2 − 3 = 2 1 − r = 2 1 − 2 2 − 3 = 2 3 − 1
Therefore a + b + c = 3 − 1 + 2 = 4 .