It's All Squares 2

$\tan(60^{\circ}) = \sqrt{3} = \dfrac{a}{x} \implies x = \dfrac{a}{\sqrt{3}}$

and

$\tan(60^{\circ}) = \sqrt{3} = \dfrac{na}{y} \implies y = \dfrac{n}{\sqrt{3}}a$

$\implies a(\dfrac{n + 1}{\sqrt{3}} + \dfrac{n(n + 1)}{2}) = 1 \implies$ $a(n + 1)(2 + \sqrt{3}n) = 2\sqrt{3}$

$\implies a = \dfrac{2\sqrt{3}}{(n + 1)(2 + \sqrt{3}n)}$

$\implies$

$A_{T} = a^2\sum_{j = 1}^{n} j^2 =a^2\dfrac{n(n + 1)(2n + 1)}{6} \implies$

$\dfrac{A_{T}}{a} = a\dfrac{n(n + 1)(2n + 1)}{6} = \dfrac{n(2n + 1)}{\sqrt{3}(2 + \sqrt{3}n)} = \dfrac{18(2\sqrt{3} - 1)}{11\sqrt{3}}$

$\implies 11n(2n + 1) = 18(2\sqrt{3} - 1)(2 + \sqrt{3}n)$

$\implies 22n^2 + 11n = 18(4\sqrt{3} - 2) + 18(6 - \sqrt{3})n \implies$

$22n^2 - (97 - 18\sqrt{3})n - (72\sqrt{3} - 36) = 0 \implies n = 4, n = -\dfrac{9(2\sqrt{3} - 1)}{22}$

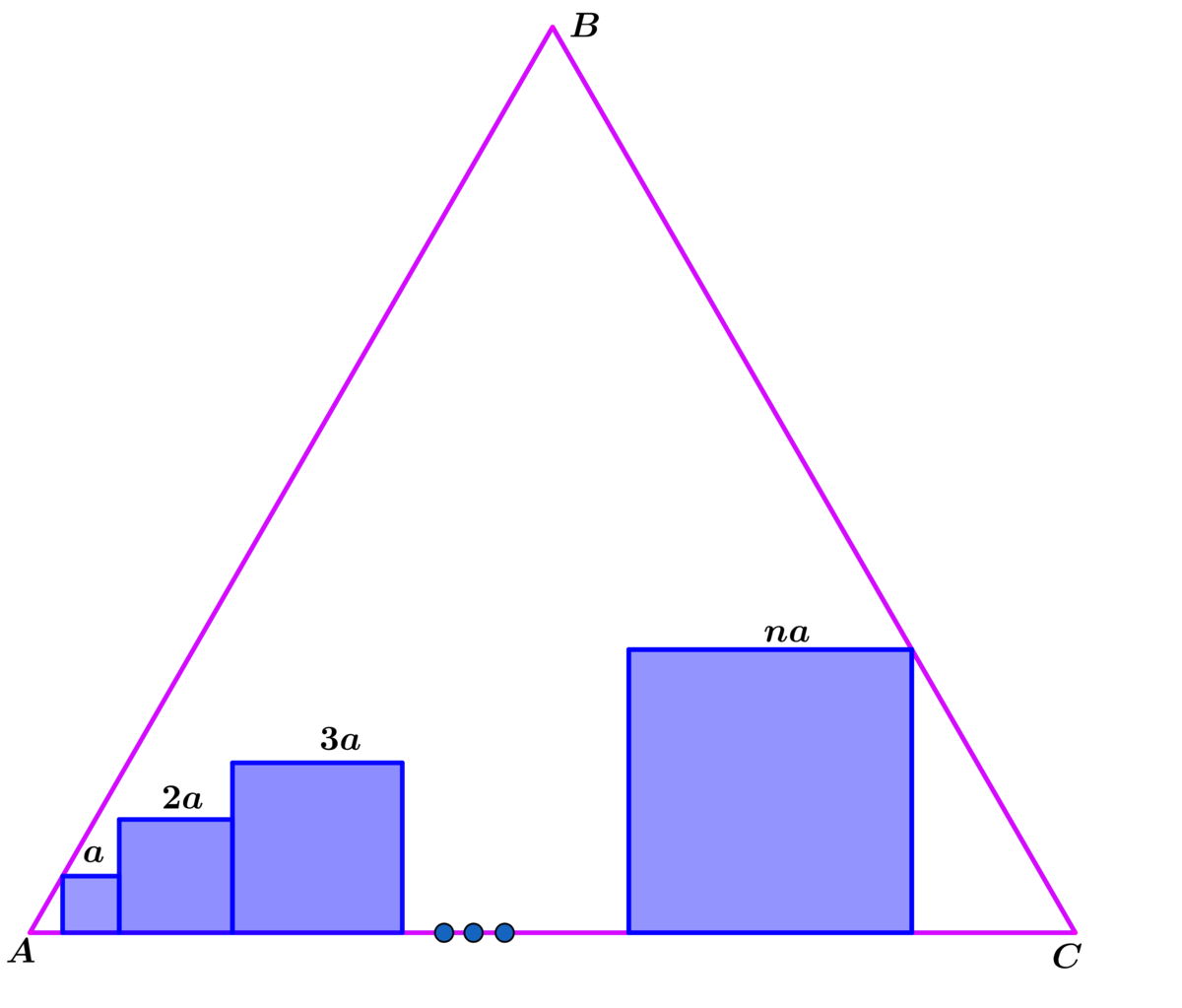
Since $n$ is a positive integer we choose $\boxed{n = 4}$

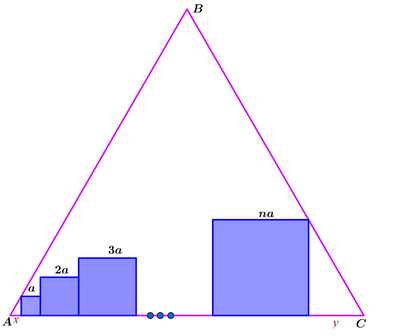
Let the two ends of line $AC$ not covered by the bases of squares be $\red x$ and $\red y$ as shown in the figure. Then $x = a \cot 60^\circ = \dfrac a{\sqrt 3}$ and $y = na \cot 60^\circ = \dfrac {na}{\sqrt 3}$ . From $AC=1$ , we have:

$\begin{aligned} \frac a{\sqrt 3} + a + 2a + 3a + \cdots + na + \frac {na}{\sqrt 3} & = 1 \\ \frac a{\sqrt 3} + \frac {n(n+1)a}2 + \frac {na}{\sqrt 3} & = 1 \\ (n+1)\left(\frac n2 + \frac 1{\sqrt 3}\right)a & = 1 \\ \frac {(n+1)(\sqrt 3n+2)a}{2\sqrt 3} & = 1 \\ \implies a & = \frac {2\sqrt 3}{(n+1)(\sqrt 3n+2)} \end{aligned}$

Now we have $A_T = a^2 + (2a)^2 + (3a)^2 + \cdots + (na)^2 = \dfrac {n(n+1)(2n+1)}6a^2$ . And

$\begin{aligned} \frac {A_T}a & = \frac {18(2\sqrt 3-1)}{11\sqrt 3} \\ \frac {n(n+1)(2n+1)}6a & = \frac {18(2\sqrt 3-1)(2\sqrt 3+1)}{11\sqrt 3(2\sqrt 3+1)} \\ \frac {n(n+1)(2n+1)}6 \cdot \frac {2\sqrt 3}{(n+1)(\sqrt 3n+2)} & = \frac {18 \cdot 11}{11(6+\sqrt 3)} \\ \frac {n(2n+1)}{\sqrt 3(\sqrt 3n+2)} & = \frac {18}{6+\sqrt 3} \\ \frac {n(2n+1)}{3n+2\sqrt 3} & = \frac {36}{12+2\sqrt 3} \\ \implies n & = \boxed 4 \end{aligned}$