It's All Squares 3 !
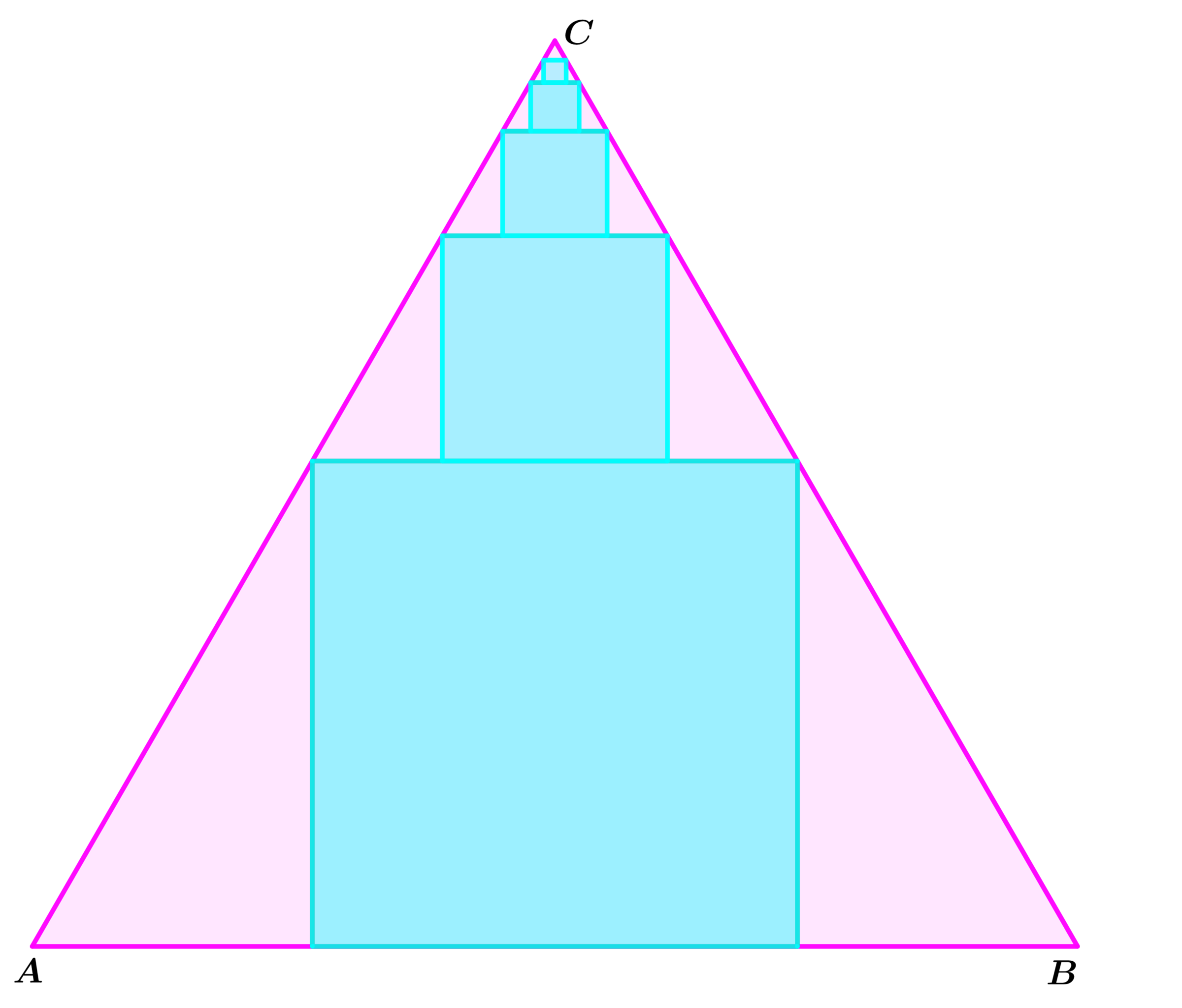
In equilateral with side length , extend the stacked inscribed squares to an infinite number of squares.
Let be a side of the initial square(largest square) and the total area of all the squares.
If , where and are coprime positive integers, find .
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 − a 1 2 a 1 = tan ( 6 0 ∘ ) = 3 ⟹ a 1 = 2 + 3 3
and
a 1 − a 2 2 a 2 = tan ( 6 0 ∘ ) = 3 ⟹ a 2 = 2 + 3 3 a 1 = ( 2 + 3 3 ) 2
a 2 − a 3 2 a 3 = 3 ⟹ a 3 = 2 + 3 3 a 2 = ( 2 + 3 3 ) 3
In General for each positive integer n we have: a n = ( 2 + 3 3 ) n
⟹
S = ∑ n = 1 ∞ a n 2 = ( 2 + 3 3 ) 2 ( 2 2 + 3 ) =
2 3 ( 2 + 3 1 ) = 2 3 ( 2 + 3 3 ) =
2 3 a 1 = h e i g h t △ A B C ∗ a 1 ⟹ a 1 S = h e i g h t △ A B C = 2 3 = β α
⟹ α + β = 5 .