It's All Squares

Level 2

The problem below is a brillant problem of the week that I slightly modified.

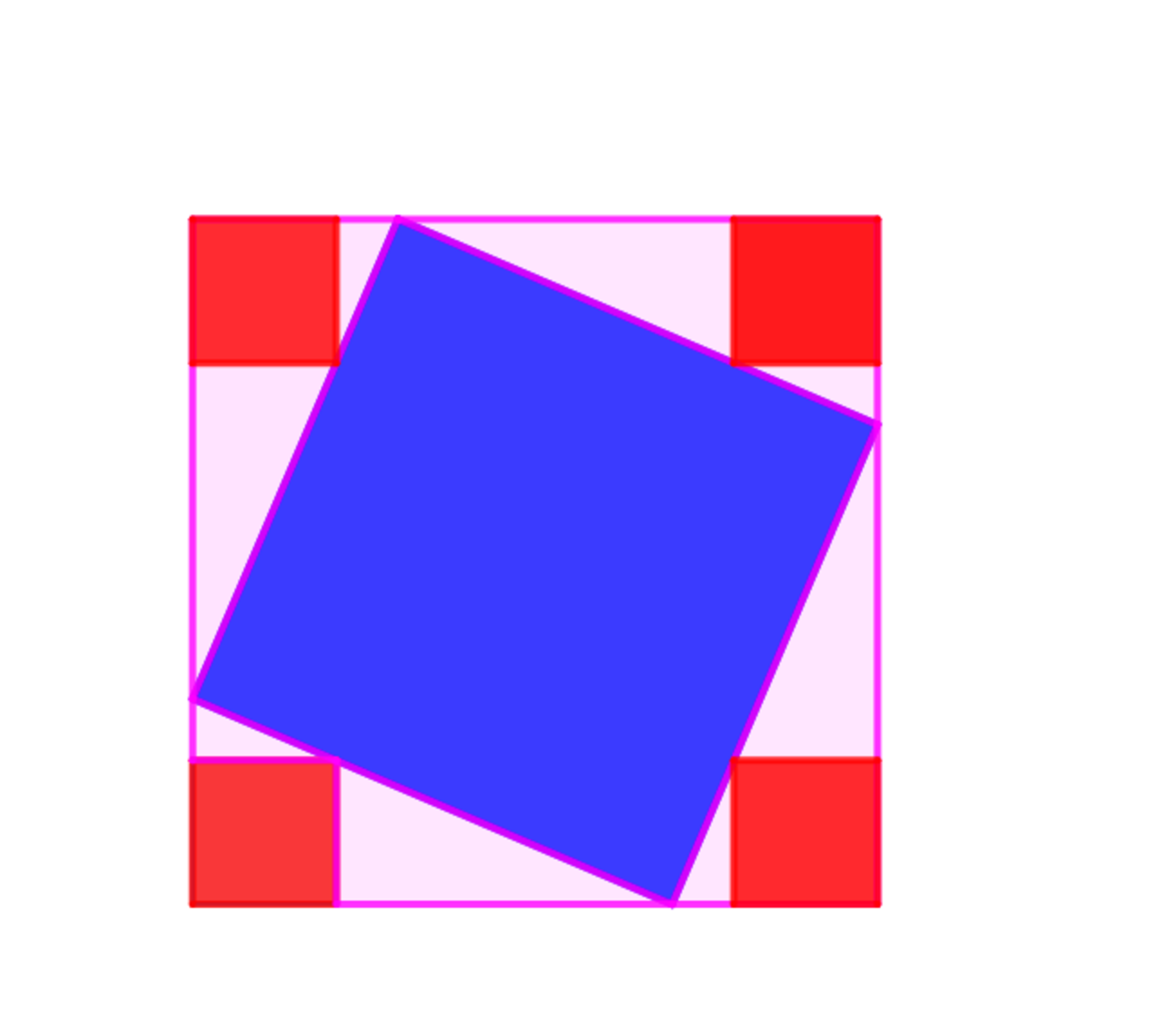
The blue square touches each side of the largest square and each of the 4 red squares at the corners of the largest square touch the blue square and the largest square is a unit square.

The unit square is the square in the Cartesian plane with corners at the four points ( 0 , 0 ) , ( 1 , 0 ) , ( 0 , 1 ) (0, 0), (1, 0), (0, 1) , and ( 1 , 1 ) (1, 1) .

Let ( 1 2 < c < 1 ) (\dfrac{1}{\sqrt{2}} < c < 1) .

If c c is a side of the blue square and the sum of the areas of the red squares are A = ∑ j = 1 4 A j = c 4 + 1 − ( 2 + 1 2 ) 2 A = \sum_{j = 1}^{4} A_{j} = c^4 + 1 - (\dfrac{\sqrt{2} + 1}{2})^2

(1): Find the value of c c .

Let ( 1 ≤ j ≤ 4 ) (1 \leq j \leq 4) .

(2): Find the coordinates ( x j , y j ) (x_{j},y_{j}) , where each of the 4 red squares at the corners of the largest square touch the blue square.

Find ∏ j = 1 4 x j + ∏ j = 1 4 y j \prod_{j = 1}^{4} x_{j} + \prod_{j = 1}^{4} y_{j} to eight decimal places.


The answer is 0.02751975.

Rocco Dalto by Rocco Dalto , 67, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Rocco Dalto
Jul 24, 2018

Let the side of the largest square have a length of 1 1 .

⟹ 1 = 2 y ( 1 − y ) + c 2 ⟹ 2 y 2 − 2 y + 1 − c 2 = 0 ⟹ y = 1 ± 2 c 2 − 1 2 \implies 1 = 2y(1 - y) + c^2 \implies 2y^2 - 2y + 1 - c^2 = 0 \implies y = \dfrac{1 \pm \sqrt{2c^2 - 1}}{2} where y 1 = 1 + 2 c 2 − 1 2 y_{1} = \dfrac{1 + \sqrt{2c^2 - 1}}{2} and y 2 = 1 − 2 c 2 − 1 2 y_{2} = \dfrac{1 - \sqrt{2c^2 - 1}}{2} and ( 1 2 < c < 1 ) (\dfrac{1}{\sqrt{2}} < c < 1) .

Using similar right triangles below we obtain:

y 1 − x x = x y 2 − x ⟹ y 1 y 2 − ( y 1 + y 2 ) x + x 2 = x 2 ⟹ \dfrac{y_{1} - x}{x} = \dfrac{x}{y_{2} - x} \implies y_{1}y_{2} - (y_{1} + y_{2})x + x^2 = x^2 \implies

x = y 1 y 2 y 1 + y 2 = 1 − c 2 2 ⟹ A = 4 ( 1 − c 2 2 ) 2 = ( 1 − c 2 ) 2 = c 4 + 1 − ( 2 + 1 2 ) 2 \boxed{x = \dfrac{y_{1}y_{2}}{y_{1} + y_{2}} = \dfrac{1 - c^2}{2}} \implies A = 4(\dfrac{1 - c^2}{2})^2 = (1 - c^2)^2 = c^4 + 1 - (\dfrac{\sqrt{2} + 1}{2})^2

⟹ 1 − 2 c 2 + c 4 = c 4 + 1 − ( 2 + 1 2 ) 2 ⟹ 2 c 2 = ( 2 + 1 2 ) 2 ⟹ c = 2 + 1 2 2 \implies 1 - 2c^2 + c^4 = c^4 + 1 - (\dfrac{\sqrt{2} + 1}{2})^2 \implies 2c^2 = (\dfrac{\sqrt{2} + 1}{2})^2 \implies \boxed{c = \dfrac{\sqrt{2} + 1}{2\sqrt{2}}} .

For each ( x j , y j ) (x_{j},y_{j}) , where ( 1 ≤ j ≤ 4 ) (1 \leq j \leq 4) :

The coordinates of the four points are: ( x , x ) , ( 1 − x , x ) , ( x , 1 − x ) , ( 1 − x , 1 − x ) ⟹ ∏ j = 1 4 x j = ( x ( 1 − x ) ) 2 = ( ( 1 − c 2 2 ) ( 1 + c 2 2 ) ) 2 = 1 16 ( 47 − 12 2 64 ) 2 (x,x), (1 - x, x), (x,1 - x),(1 - x,1 - x) \implies \prod_{j = 1}^{4} x_{j} = (x(1 - x))^2 = ((\dfrac{1 - c^2}{2})(\dfrac{1 + c^2}{2}))^2 = \dfrac{1}{16}(\dfrac{47 - 12\sqrt{2}}{64})^2

= ∏ j = 1 4 y j ⟹ ∏ j = 1 4 x j + ∏ j = 1 4 y j = 1 8 ( 47 − 12 2 64 ) 2 ≈ 0.02751975 = \prod_{j = 1}^{4} y_{j} \implies \prod_{j = 1}^{4} x_{j} + \prod_{j = 1}^{4} y_{j} = \dfrac{1}{8}(\dfrac{47 - 12\sqrt{2}}{64})^2 \approx \boxed{0.02751975} .

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...