It's All Tangents!
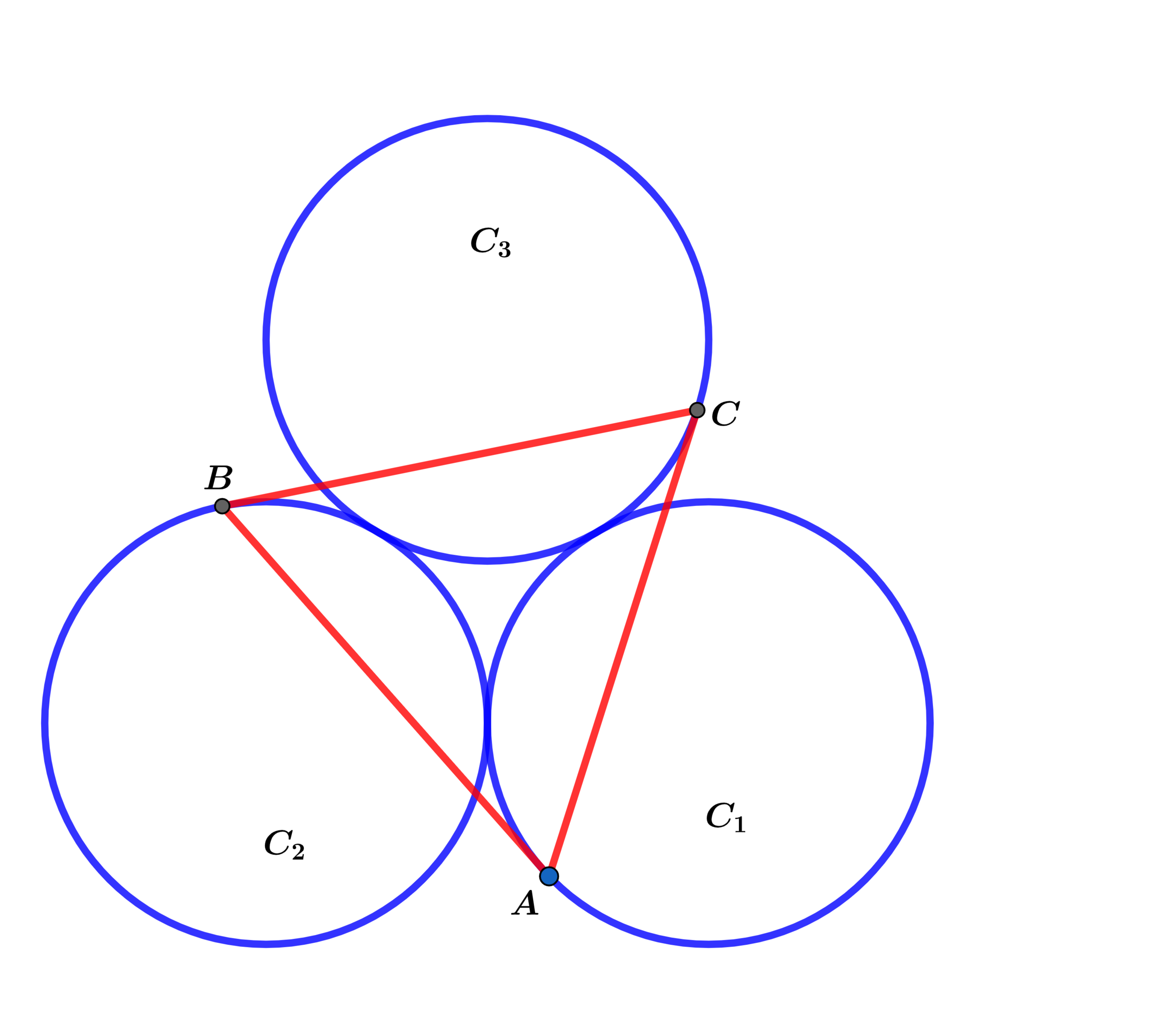
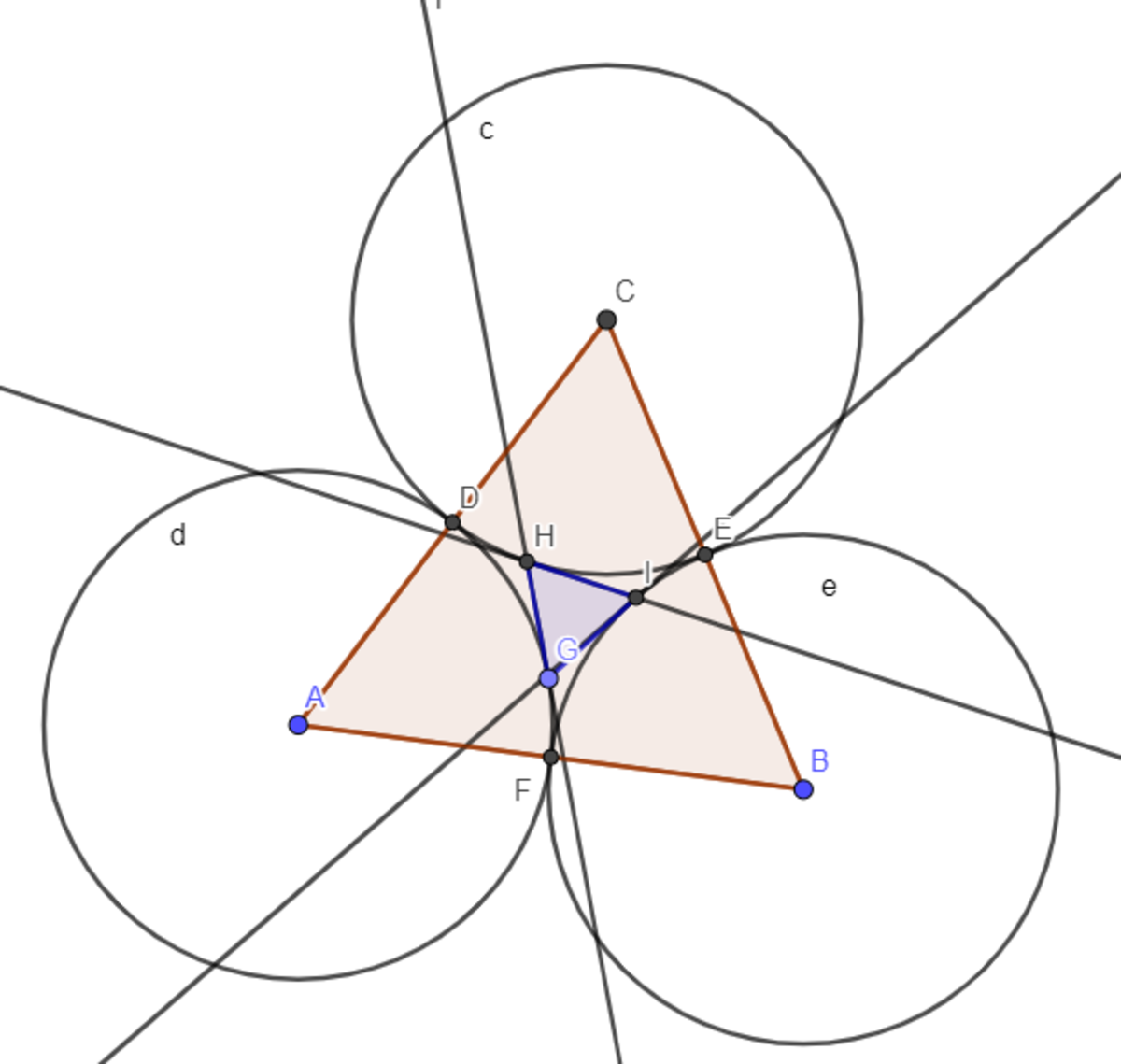
The three congruent circles C 1 , C 2 and C 3 each have radius r and are tangent to each other as shown above. A B is tangent to C 1 at point A , B C is tangent to C 2 at point B and A C is tangent to C 3 at point C and △ A B C formed is an equilateral triangle.
If r 2 A △ A B C = b a ( c + d ) , where a , b , c and d are coprime positive integers, find a + b + c + d .
The answer is 37.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Label the diagram as follows, with r = C D = D E :
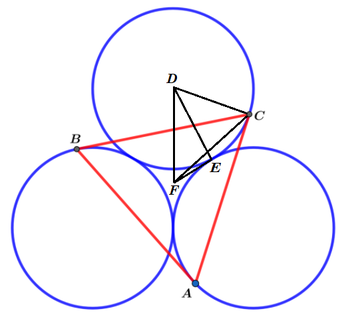
Since ∠ D F E = 6 0 ° , ∠ D E F = 9 0 ° , and D E = r , D F = sin 6 0 ° D E = 3 2 3 r .
Since ∠ F C A = 3 0 ° and ∠ D C A = 9 0 ° , ∠ D C F = ∠ D C A − ∠ F C A = 9 0 ° − 3 0 ° = 6 0 ° .
By the law of cosines on △ C D F , D F 2 = C D 2 + C F 2 − 2 ⋅ C D ⋅ C F ⋅ cos ∠ D C F , or ( 3 2 3 r ) 2 = r 2 + C F 2 − 2 ⋅ r ⋅ C F ⋅ cos 6 0 ° , which solves to C F = ( 2 1 + 6 2 1 ) r for C F > 0 .
The area of △ A B C is then A △ A B C = 3 ⋅ A △ C F A = 3 ⋅ 2 1 ⋅ C F 2 ⋅ sin 1 2 0 ° = 3 ⋅ 2 1 ⋅ ( 2 1 + 6 2 1 ) 2 r 2 ⋅ 2 3 = 8 3 ( 5 + 2 1 ) r 2 .
Therefore, a = 3 , b = 8 , c = 5 , d = 2 1 , and a + b + c + d = 3 7 .
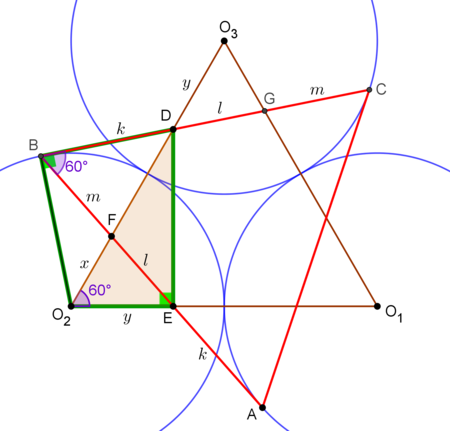 Denote by
O
1
,
O
2
and
O
3
the centers of circles
C
1
,
C
2
and
C
3
respectively. These three points form an equilateral triangle. Let
D
be the point of intersection of
B
C
and
O
2
O
3
. Let
E
be the point of intersection of
A
B
and
O
1
O
2
. Let
F
be the point of intersection of
A
B
and
O
2
O
3
. Let
G
be the point of intersection of
B
C
and
O
1
O
3
, as shown on the figure.
Denote by
O
1
,
O
2
and
O
3
the centers of circles
C
1
,
C
2
and
C
3
respectively. These three points form an equilateral triangle. Let
D
be the point of intersection of
B
C
and
O
2
O
3
. Let
E
be the point of intersection of
A
B
and
O
1
O
2
. Let
F
be the point of intersection of
A
B
and
O
2
O
3
. Let
G
be the point of intersection of
B
C
and
O
1
O
3
, as shown on the figure.
Since ∠ D B E = ∠ D O 2 E =60{}^\circ), points B , D , E and O 2 are concyclic. B C is tangent to C 2 , thus ∠ O 2 B D = 9 0 ∘ and hence, ∠ O 2 E D = 1 8 0 ∘ − ∠ O 2 B D = 9 0 ∘ .
This means that △ O 2 D E is a 9 0 ∘ - 6 0 ∘ - 3 0 ∘ triangle, therefore, O 2 D = 2 O 2 E .
Due to the threefold symmetry of the compound shape of the two equilateral triangles, segments O 2 E and O 3 D are congruent. Let O 2 E = O 3 D = y . Then O 2 D = 2 y , so we have O 2 O 3 = O 2 D + D O 3 ⇒ 2 r = 2 y + y ⇒ y = 3 2 r Using Pythagorean theorem on △ O 2 D E
D E 2 = O 2 D 2 − O 2 E 2 = ( 2 y ) 2 − y 2 = 3 y 2 ⇒ D E = y 3 ⇒ D E = 3 2 r Again, because of the symmetry, ( B D , A E ) , ( D G , E F ) and ( G C , B F ) are pairs of congruent segments. Label B D , A E by k , D G , E F by l and G C , B F by m .
By Pythagorean theorem on △ O 2 B D
B D 2 + O 2 B 2 = O 2 D 2 ⇒ k 2 + r 2 = ( 2 y ) 2 ⇒ k 2 + r 2 = 9 1 6 r 2 ⇒ k = 3 r 7 ( 1 )
From the similarity of triangles △ O 2 E F and △ B D F we get
B F O 2 F = B D O 2 E ⇒ m x = k y = ( 1 ) 3 r 7 3 2 r = 7 2 ⇒ x = 7 2 m ( 2 ) Likewise, from the similarity of triangles △ O 2 B F and △ E D F we have
E F O 2 F = D F B F = D E O 2 B ⇒ l x = 3 3 r − x m = 3 2 r 3 r = 2 3 ⇒ ⎩ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎧ x = 2 3 l ( 3 ) 0 l m = x ( 3 3 r − x ) ( 4 )
( 2 ) , ( 3 ) ⇒ x 2 = 7 3 l m ⇒ ( 4 ) x 2 = 7 3 x ( 3 4 r − x ) ⇒ x = 0 x = 7 3 ( 3 4 r − x ) which solves to x = 3 2 1 − 3 r ( 5 ) Now,
( 2 ) ⇒ ( 5 ) m = 2 7 ⋅ 3 2 1 − 3 r ⇒ m = 6 7 3 − 3 7 r ( 6 )
( 3 ) ⇒ ( 5 ) l = 3 2 ⋅ 3 2 1 − 3 r ⇒ l = 3 2 ( 7 − 3 ) r ( 7 )
Calculating the length of the side of the red triangle,
( 1 ) , ( 6 ) , ( 7 ) ⇒ B C = k + l + m = 3 7 r + 3 2 ( 7 − 3 ) r + 6 7 3 − 3 7 r ⇒ B C = 2 7 + 3 r Finally,
A △ A B C = 4 3 B C 2 = 4 3 ( 2 7 + 3 ) 2 r 2 = 8 3 ( 5 + 2 1 ) r 2 ⇒ r 2 A △ A B C = 8 3 ( 5 + 2 1 ) .
For the answer, a = 3 , b = 8 , c = 5 , d = 2 1 , thus a + b + c + d = 3 7 .
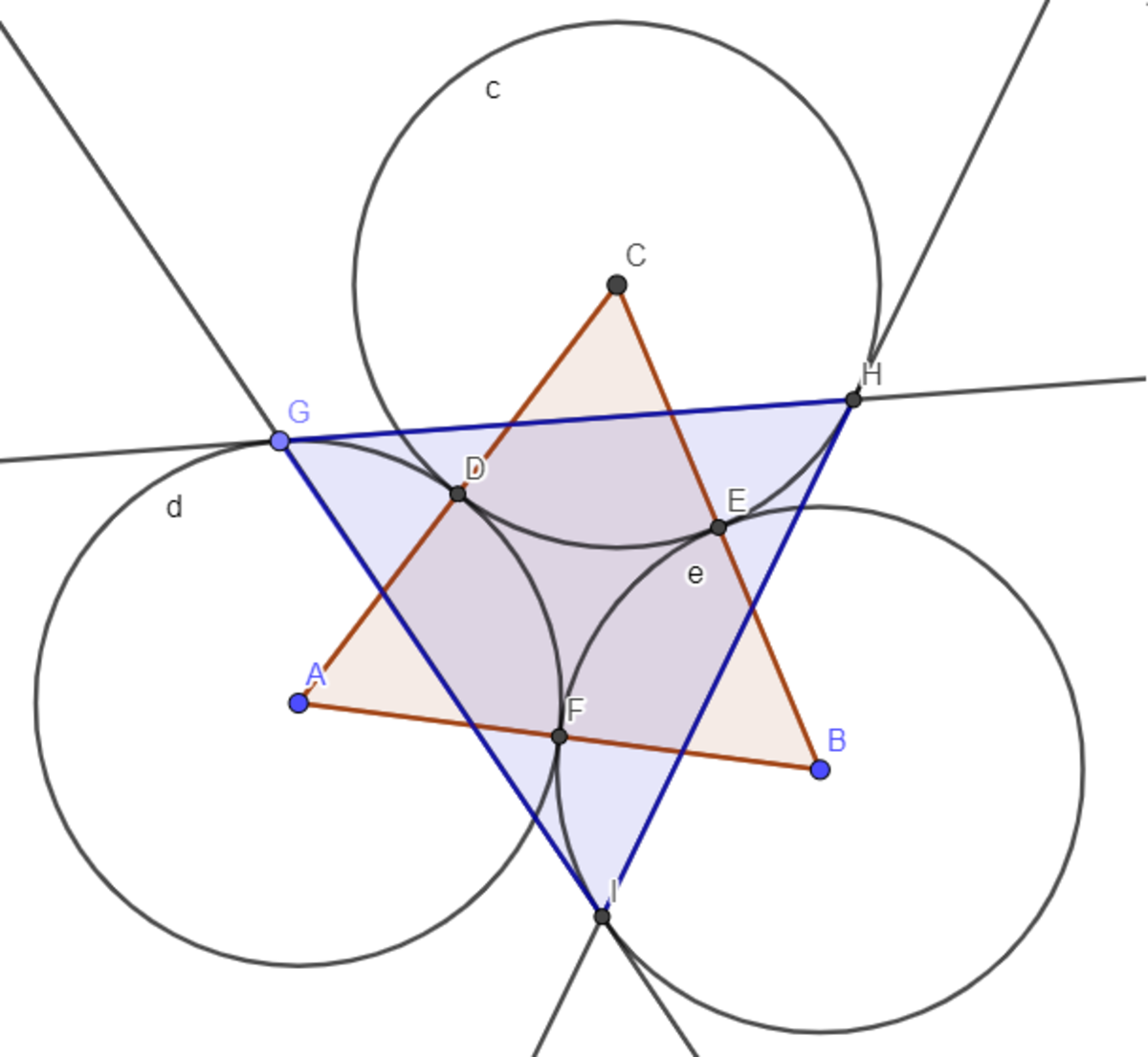
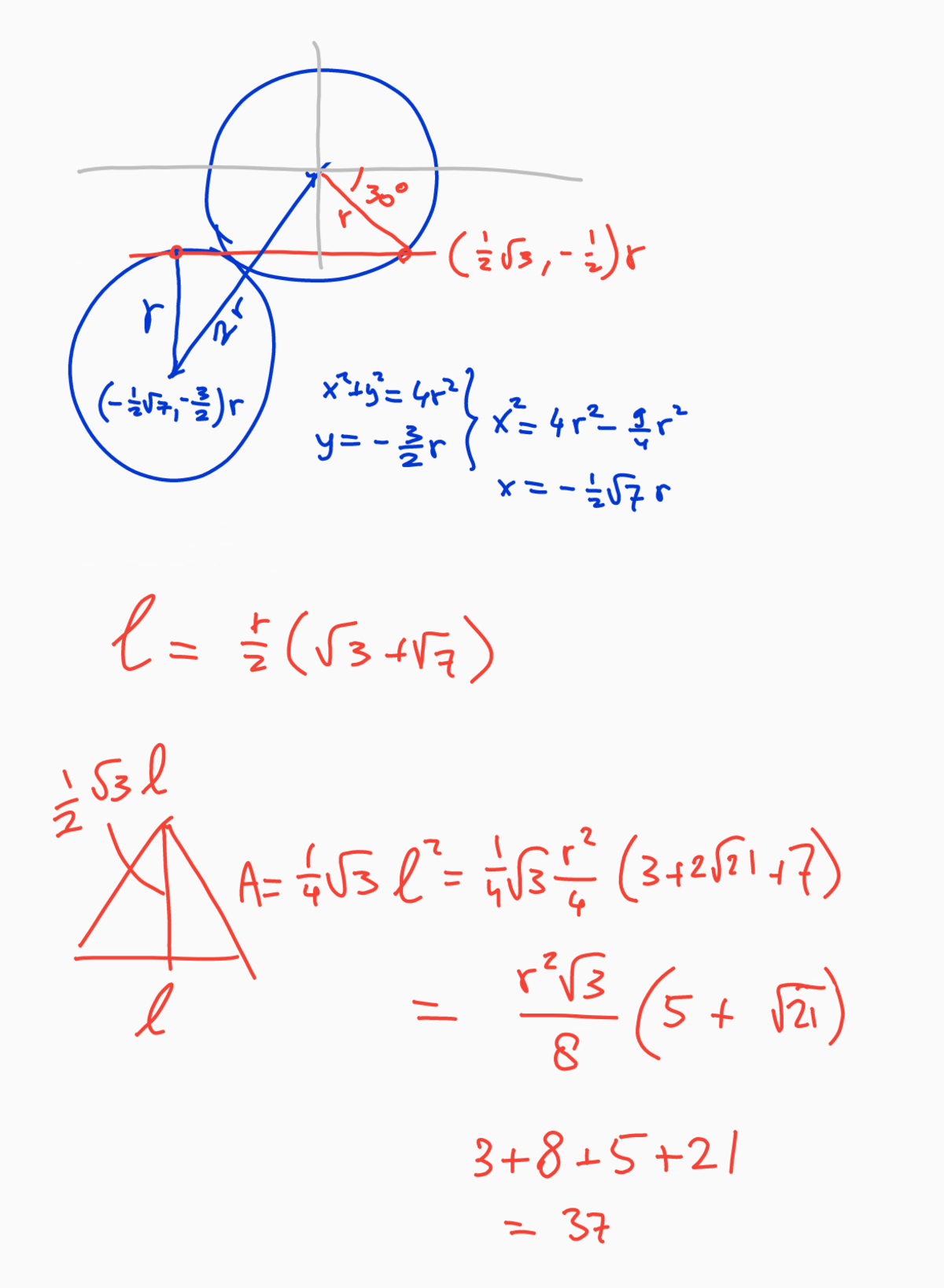
Extend radii O B and C P so that O B and C P intersect at D .
B C is tangent to circle C 2 at B ⟹ ∠ O B C and ∠ D B C are right angles ⟹ △ D B C is a right triangle and A C is tangent to circle C 3 at C ⟹ ∠ D C A is a right angle and △ A B C is an equilateral triangle ⟹ m ∠ B C A = 6 0 ∘ ⟹ m ∠ D C B = 3 0 ∘ ⟹ △ D B C is a 3 0 − 6 0 − 9 0 right triangle.
Let D B = x ⟹ B C = 3 x and C D = 2 x
C 2 and C 3 are tangent to each other as shown above ⟹ O P = 2 r and each radii O B = P C = r ⟹ P D = 2 x − r and O D = x + r .
Using the law of cosines on △ D O P formed we have:
4 r 2 = ( 2 x − r ) 2 + ( x + r ) 2 − 2 ( 2 x − r ) ( x + r ) cos ( 6 0 ∘ ) = 3 x 2 − 3 r x + 3 r 2 ⟹ 3 x 2 − 3 r x − r 2 = 0 ⟹
x = 6 3 + 2 1 r dropping the negative root
⟹ B C = 3 x = 2 3 3 + 2 1 r ⟹ the area of isosceles △ A B C is
A △ A B C = 4 3 ( 2 3 3 + 2 1 ) 2 r 2 = 8 3 ( 5 + 2 1 ) r 2 ⟹
r 2 A △ A B C = 8 3 ( 5 + 2 1 ) = b a ( c + d ) ⟹ a + b + c + d = 3 7 .