It's All Tetrahedrons 2 - Reposted
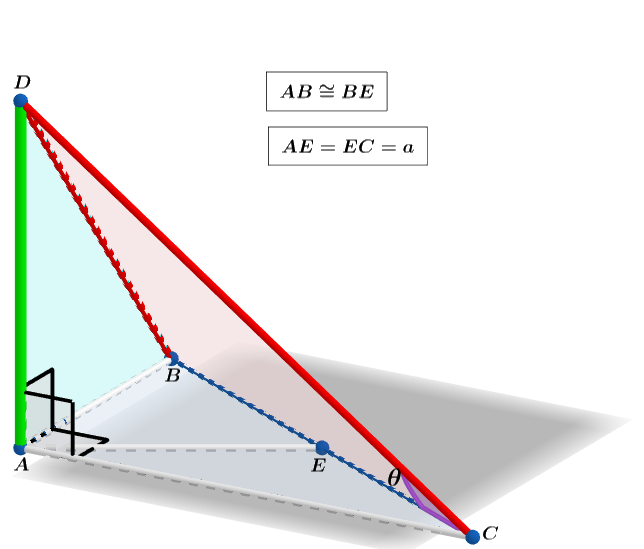
In the irregular tetrahedron above, find the that minimizes the triangular face when the volume of the tetrahedron is held constant.
The answer is 45.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
△ A E C is an isosceles triangle ⟹ E M is the perpendicular bisector of base A C ⟹ △ M E C is a right triangle and A M = M C .
Since ∠ A C B is a common angle to both right triangle A B C and M E C ⟹ △ A B C ∼ △ M E C ⟹ m 2 m = a x + a ⟹ x = a and the pythagorean theorem in △ A B C ⟹ y = 2 m = 3 a .
Let h be the height of the tetrahedron.
v = − 3 a i + a j + 0 k
u = − 3 a i + 0 j + h k
⟹ u X v = − a h i − 3 a h j − 3 a 2 k ⟹ ∣ u X v ∣ = a 4 h 2 + 3 a 2 and ∣ u ∣ = 3 a 2 + h 2
⟹ d = 3 a 2 + h 2 a 4 h 2 + 3 a 2 ⟹ A △ B C D = 2 1 a 4 h 2 + 3 a 2
Let A = 2 1 a 4 h 2 + 3 a 2
The volume V = 2 3 1 a 2 h = k ⟹ h = a 2 2 3 k ⟹ A ( a ) = a 4 8 k 2 + 3 a 6 ⟹
d a d A = a 2 4 8 k 2 + 3 a 6 6 a 6 − 4 8 k 2 = 0 a = 0 ⟹ a = 2 k 3 1 ⟹ h = 3 k 3 1
d a d A < 0 when a < 2 k 3 1 and d a d A > 0 when a > 2 k 3 1 ⟹ minimum at a = 2 k 3 1 .
Let m ∠ B C D = θ .
For cos ( θ ) :
C D = 3 k 3 1 , B C = 2 2 k 3 1 and B D = 5 k 3 1
⟹ 5 = 1 7 − 6 8 cos ( θ ) ⟹ cos ( θ ) = 2 1 ⟹ θ = 4 5 ∘ .