It's All Volumes!
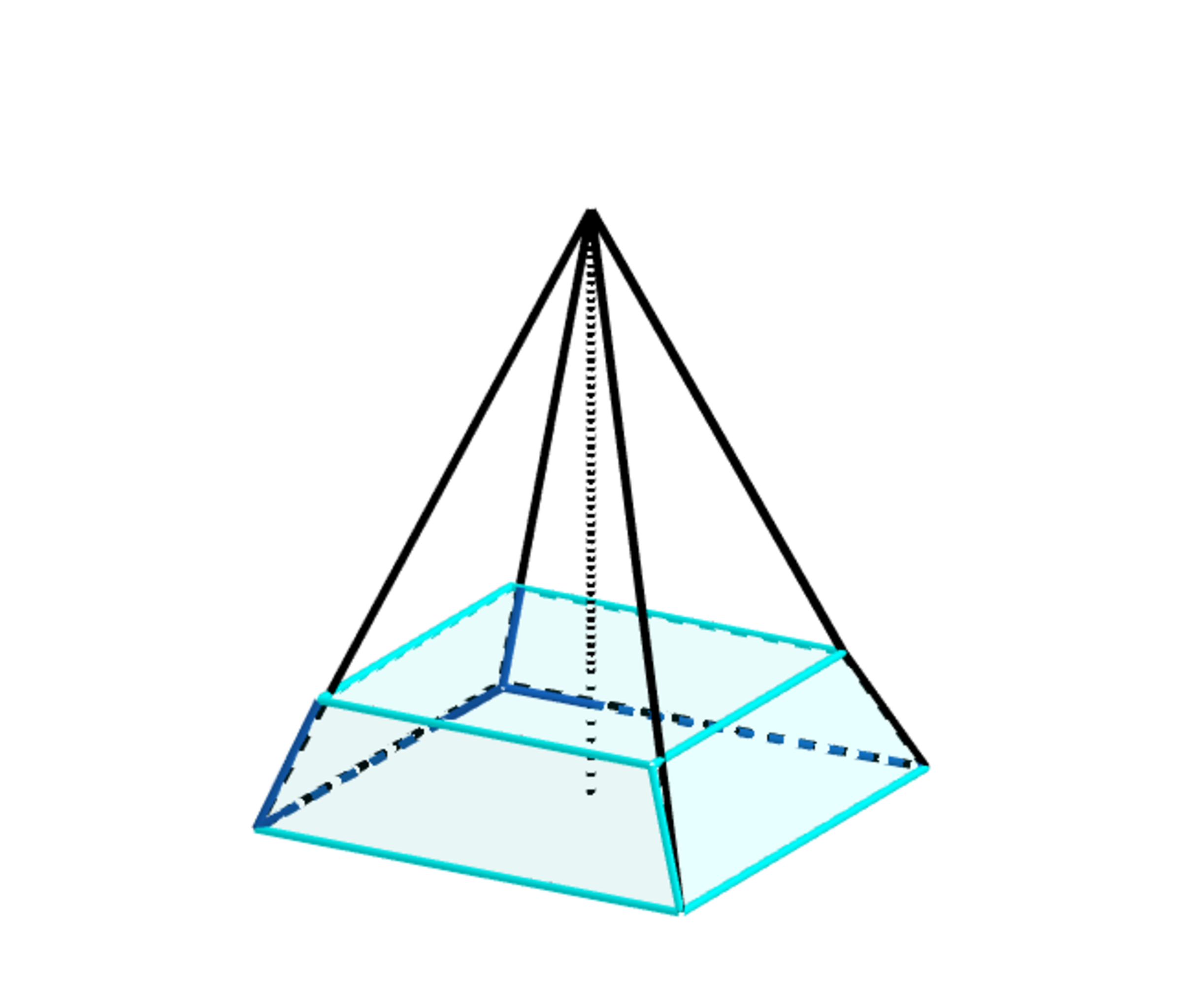
In the first diagram the filled water is cm from the vertex of the square pyramid.
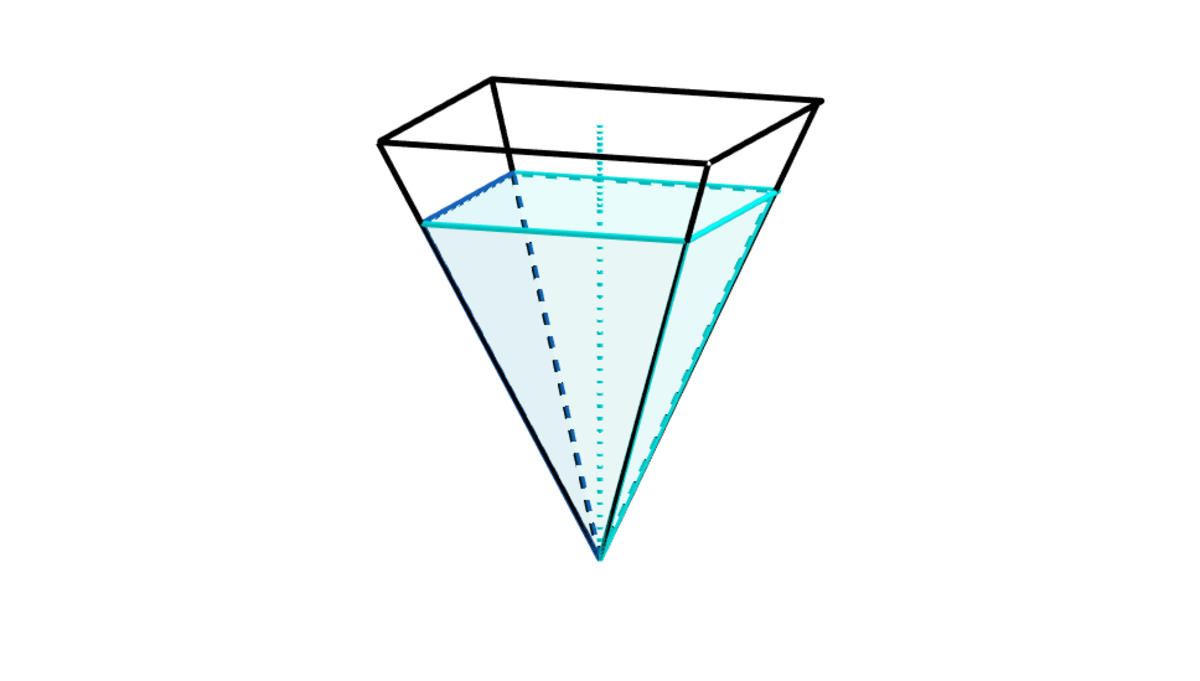
In the second diagram the square pyramid is turned upside down and the filled water is cm from the base of the square pyramid.
What is the height of the pyramid?
The answer is 10.2195.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Clearly in both cases the volume is the same.
In both diagrams below replace R Q = x by 2 x and S T = x 1 and M N = x 2 by 2 x 1 and 2 x 2 respectively.
For volume V 1 :
Using the above diagram △ P T S ∼ △ P R Q ⟹ x 1 1 6 = x 2 h ⟹ x 1 = h 8 x ⟹
V 1 = 3 1 ( x 2 − 8 ( h 2 6 4 x 2 ) ) = 3 1 x 2 ( h 2 h 3 − 5 1 2 )
For V 2 :
Using the second diagram above △ P ′ M N ∼ △ P ′ R Q ⟹ x 2 h − 2 = x h
⟹ x 2 = h ( h − 2 ) x ⟹ V 2 = 3 1 x 2 h 2 ( h − 2 ) 3
V 1 = V 2 ⟹ h 3 − 5 1 2 = h 3 − 6 h 2 + 1 2 h − 8 ⟹ h 2 − 2 h − 8 4 = 0 ⟹
h = 1 + 8 5 choosing the positive root.
∴ h = 1 + 8 5 ≈ 1 0 . 2 1 9 5 .