It's as hard as 1-2-3

A circle with center O has two points A , B on its circumference and one point P inside the circle such that A P = 1 , B P = 2 , O P = 3 , and ∠ A P B = 9 0 ∘ . If the area of the circle can be expressed as ( d a + b c ) π for positive integers a , b , c , d such that c is square-free and a , b are coprime with d , then find the value of a + b + c + d .
The answer is 83.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
17 solutions
Well, since no one else wants to prove that α is obtuse, then I will. Suppose, to the contrary that α is acute. For brevity, let β = ∠ O P B . Then we have two cases:
Case 1: α is acute, β is obtuse
 Acute Case
Acute Case
Since ∠ O P A is acute, then applying the Cosine Law on △ O P A gives us O A = O P 2 + P A 2 − 2 ( O P ) ( P A ) c o s ( α ) , and therefore O A < 1 2 + 3 2 = 1 0 .
However, we also have that β is obtuse. Therefore, applying the Cosine Law on △ O P B gives us O B > 2 2 + 3 2 = 1 3 . This is a contradiction since now we have 1 0 > O A = O B > 1 3 .
Case 2: α is acute, β is acute
 Case 2
Case 2
Since O A > 3 > 1 , then α must be the greatest angle in △ O P A . Therefore α > 6 0 ∘ . However, by similar logic we also get β > 6 0 ∘ . But this is a contradiction since in this case, α + β − 9 0 ∘ .
Either way, we see that α cannot be acute. Therefore α is obtuse. QED
https://brilliant.org/discussions/thread/can-you-help/?ref_id=498718
.
.
it is solved by default LOL
thanks for solving
Nice! This is great! :D
But u made it
Log in to reply
I made the question. However, I did not have a solution in mind, so I had to solve the question I proposed just like all of you. Along with the solution writing, double and triple checking work, and making the problem itself from the cauldron of mathematical ideas in the universe, it took a long time.
Anyways, that 1.5 hour record was easily beat by Directrix will Drive you Delirious
brilliant! Please make more! Job well done!
Is "alpha seems to be an obtuse angle" really a justification? "It seems to be" doesn't prove that "it is". Our intuition could be wrong. Even the absolutely obvious statements were proved in the Euclid's book "Elements". So you should come up with the proof of the fact to make this a perfectly valid solution.
In all seriousness though, could you tell me a proof of the alpha angle being obtuse? Thanks.
Seriously, it took me aboit 15 minutes.
I did almost same .just instead of eliminating r ,u can eliminate alpha.anyways gd sum.
i solved it exactly the same lengthy way! :P but i liked the problem~! :)
You should check out my solution and see what I did. ( Just copied your statement, if you remember. LOL )
Let M be the midpoint of the A B , whose length is 1 2 + 2 2 = 5 . Since O A = O B , therefore O M ⊥ A B . Let N denote the intersection of A P , O M .
Since △ N A M ∼ △ B A P , by their corresponding side ratio equality we have A M ∗ A B = A N ∗ A P ⇒ 2 5 5 = 1 ∗ A N = 2 5 ⇒ P N = 2 5 − 1 = 2 3 .
At this point, one may be motivated to use the laws of cosine on △ O P N since c o s ∠ O N P = − c o s ∠ A N M = − c o s ∠ A B P = − 5 2 , that is what I decided to do to find the length of O N , which is denoted by x :
O P 2 = 9 = P N 2 + x 2 − 2 x P N c o s ∠ O N P = 4 9 + x 2 + 5 6 x
Solving this quadratic gives x = 2 5 3 1 9 − 6 (of course..after omitting the negative).
By the similarity again we have N M = A M ∗ 2 = 5 , hence O M = O N + N M = 2 5 3 1 9 + 4 and now we can use the Pythagorean theorem to find the radius squared, which is 5 5 3 + 6 1 9 . Since the area of a circle is pi*radius squared, this is the expression we need, thus our answer is 5 3 + 6 + 1 9 + 5 = 8 3
Clever solution! Much shorter than my page-long solution. Kudos for the ingenuity.
Log in to reply
Thanks..a shorter solution doesn't really mean anything..although mine has less trig but I think yours is a more natural approach. Well that's why I enjoy doing geometry problems(especially proofs) because you just have so much freedom with the diagram and you can construct whatever you want(useful things of course..).
Btw your problems have been great and fun, keep them coming!
Much shorter solution. BTW, why is that triangle NAM is similar to triangle BAP?
Log in to reply
both triangles share ∠ P A B and ∠ A M N = ∠ A P B = 9 0
Well I found a solution using Pythagoras' Theorem. Here it goes
 Construction
Construction
Now we use Pythagoras' Theorem on the three right-triangles,
r 2 = y 2 + ( x + 2 ) 2 − − − ( i )
r 2 = x 2 + ( y + 1 ) 2 − − − ( i i )
x 2 + y 2 = 3 2 − − − ( i i i )
From ( i ) and ( i i ) we get 3 + 4 x = 2 y → y = 2 3 + 2 x − − − ( i v )
Using this in ( i i i ) we get a quadratic in x which is 2 0 x 2 + 2 4 x − 2 7 = 0 . Taking the positive root(since x > 0 ) we have x = 1 0 − 6 + 3 1 9 .
Also using ( i i i ) in any of ( i ) or ( i i ) we get r 2 = 1 3 + 4 x − − ( v )
So area of circle = π r 2 = ( 1 3 + 4 x ) π = ( 5 5 3 + 6 1 9 ) π .
So a + b + c + d = 5 3 + 6 + 1 9 + 5 = 8 3 .
Congratulations. Nice out of the box solution . Just to point out. Himanshu Arora's solution is the same in p r i n c i p l e .
Lets make the solution very simple but not tricky ....
For a triangle ABC you know the cosine rule-
c o s ( A ) = 2 . A B . A C A B 2 + A C 2 − B C 2
Now we will apply the cosine rule in triangle POA and in triangle POB , for angel P in both the triangles. Also note that OA and OB is radius of circle, say OA = OB = r
Applying cosine rule we have-
c o s ( ∠ O P A ) = 6 1 0 − r 2 ⇒ ∠ O P A = cos − 1 6 1 0 − r 2
c o s ( ∠ O P B ) = 1 2 1 3 − r 2 ⇒ ∠ O P B = cos − 1 1 2 1 3 − r 2
And clearly ∠ O P A + ∠ O P B = 2 3 π
If you remember cos − 1 x + cos − 1 y = cos − 1 ( x y − ( 1 − x 2 ) ( 1 − y 2 )
Now, if cos − 1 x + cos − 1 y = 2 3 π ⇒ x y − ( 1 − x 2 ) ( 1 − y 2 ) = 0 ⇒ x 2 + y 2 = 1
Here x = ∠ O P A and y = ∠ O P B , So-
(
6
1
0
−
r
2
)
2
+
(
1
2
1
3
−
r
2
)
2
=
1
⇒
5
(
r
4
)
−
1
0
6
(
r
2
)
+
4
2
5
=
0
Using Sridharacharya Formula ,
r 2 = 1 0 1 0 6 ± 2 7 3 6 ⇒ r 2 = 1 0 1 0 6 ± 1 2 1 9 ⇒ r 2 = 5 5 3 ± 6 1 9
Now its simple to compare and get that
a = 53, b = 6, c = 19, d = 5
[Ignore negative sign, as demand of question]
⇒
a
+
b
+
c
+
d
=
8
3
Assume that the given figure is true. Draw lines parallel to PA and PB through O. Mark distance of P from these lines, x and h . Make three equations, h 2 + x 2 = 9 ; ( h + 1 ) 2 + x 2 = r 2 ; h 2 + ( x + 2 ) 2 = r 2 . Solve to get the value of r 2 as 5 6 1 9 + 5 3 . And hence get 8 3 , answer
incredible
A solution using the power of a point theorem (just Euclidean Geometry, no coordinate geometry, no trigonometry).

Let O M ⊥ P A , O N ⊥ P B , P M = x , P N = y .
M is the midpoint of A A ′ , hence M A ′ = x + 1 .
Similarly, N is the midpoint of B B ′ , hence N B ′ = y + 2 .
By power of a point theorem: P A ⋅ P A ′ = P B ⋅ P B ′ ⇒ 1 ⋅ ( 2 x + 1 ) = 2 ⋅ ( 2 y + 2 ) ⇒ x = 2 y + 2 3 ( 1 )
By Pythagorean theorem on △ O N P : O N 2 + N P 2 = O P 2 ⇒ x 2 + y 2 = 9 ( 2 ) .
Combining (1) and (2) we get the quadratic equation 5 y 2 + 6 y − 4 2 7 = 0 , which gives the positive solution y = 1 0 − 6 + 3 1 9 .
Now, the power of point P is given by the formula h = O P 2 − R 2 , (where R is the radius of the circle) and is opposite to the product P B ⋅ P B ′ , hence,
O P 2 − R 2 = − P B ⋅ P B ′ ⇒ R 2 = 9 + 2 ⋅ ( 2 y + 2 ) ⇒ R 2 = 4 y + 1 3 = 4 ⋅ 1 0 − 6 + 3 1 9 + 1 3 = 5 5 3 + 6 1 9
Thus, the area of the circle is A = R 2 ⋅ π = 5 5 3 + 6 1 9 ⋅ π , so a + b + c + d = 5 3 + 6 + 1 9 + 5 = 8 3 .
Draw line O A and O B . Since O B = O A = x and angle O P A = 2 7 0 − angle O P B , the law of cosines can be used. Let angle O P A = a .
3 2 + 1 2 − 2 ( 3 ) ( 1 ) ∗ c o s ( a ) = 3 2 + 2 2 − 2 ( 3 ) ( 2 ) ∗ c o s ( 2 7 0 − a ) . This simplifies to 3 2 + 1 2 − 2 ( 3 ) ( 1 ) ∗ c o s ( a ) = 3 2 + 2 2 + 2 ( 3 ) ( 2 ) ∗ s i n ( a ) . Let A = c o s ( a ) , then s i n ( a ) = s q r t ( 1 − A 2 ) . By substitution, 9 − 6 A = 1 3 − 1 2 ∗ s q r t ( 1 − A 2 ). By solving the quadratic, we substitute the value of A into 3 2 + 1 2 − 2 ( 3 ) ( 1 ) ∗ A = x 2 to find the square of the radius. By multiplying this by π , we obtain an expression with a , b , c , and d . Then, a + b + c + d = 8 3 .
OAB is an isosceles triangle, with a OA=OB=R the radius.
Let M be the midpoint of base AB, and so OM is the altitude on the base.
Let P(0,0) in coordinate axis. So
A(0,-1), B(2,0) and M(1,-1/2).
Slope of AB is 1/2, so slope of OM is - 2. M is on OM so, OM is Y = - 2X + 3/2.
S
i
n
c
e
O
l
i
e
s
o
n
i
t
a
s
w
e
l
l
a
s
o
n
c
i
r
c
l
e
X
2
+
Y
2
=
3
2
,
⟹
X
2
+
(
−
2
X
+
3
/
2
)
2
=
9
.
S
o
l
v
i
n
g
t
h
e
q
u
a
d
r
a
t
i
c
a
n
d
g
e
t
t
i
n
g
Y
f
r
o
m
Y
=
−
2
X
+
3
/
2
,
w
e
g
e
t
,
X
=
1
0
6
±
3
1
9
a
n
d
Y
=
1
0
3
∓
6
1
9
.
O
i
s
(
X
,
Y
)
O
i
s
t
o
l
e
f
t
a
n
d
a
b
o
v
e
P
(
0
,
0
)
,
w
e
t
a
k
e
+
s
i
g
n
f
o
r
Y
,
−
f
o
r
X
.
∴
R
2
=
O
A
2
=
(
X
−
0
)
2
+
(
Y
−
[
−
1
]
)
2
=
(
1
0
6
−
3
1
9
)
2
+
(
1
0
3
+
6
1
9
+
1
)
2
=
5
5
3
+
6
1
9
∴
a
+
b
+
c
+
d
=
8
3
we know that O B = O A so what we are going to do is finding what is equivalent to each of them and do the math :D
first of all let's assume that O P A = x and O B = r and O A = r
in Triangle O B P and from the cosine law
r 2 = 1 3 − 1 2 c o s ( 2 7 0 − x ) which is equal to
r 2 = 1 3 + 1 2 s i n ( x )
in Triangle O P A and from the cosine law
r 2 = 1 0 − 6 c o s ( x )
so we can say that
1 0 − 6 c o s ( x ) − 1 3 + 1 2 s i n ( x ) = 0
3 + 6 c o s ( x ) + 1 2 s i n ( x ) = 0
we can assume that t = t a n ( 2 x )
then s i n ( x ) = 1 + t 2 2 t and c o s ( x ) = 1 + t 2 1 − t 2
so
1 + t 2 3 + 3 t 2 + 1 + t 2 6 − 6 t 2 + 1 + t 2 2 4 t = 0
− 1 − t 2 3 t 2 − 2 4 t − 9 = 0 ... we multiply both sides by − 1 − t 2
3 t 2 − 2 4 t − 9 = 0 divide by 3 to get
t 2 − 8 t − 3 = 0
we solve and we get that
t = 4 + ( 1 9 ) and x = 1 6 6 . 3 5 5 9 1 5 2 and we know that
r 2 = 1 3 + 1 2 s i n ( x ) and it will be equal to
r 2 = 5 5 3 + 6 ( 1 9 )
so the solution will be 3 5 + 6 + 1 9 + 5 = 8 3
and that is the first solution
t = 4 − ( 1 9 ) is the second solution but then x will be acute which is refused and I don't know why ! :D ... I think this problem should have two answers
We choose P to be the Origin of the plane and A , B to be ( 0 , 1 ) , ( 2 , 0 ) respectively. The mid point M of A B must be ( 1 , 2 1 )
We have O is the intersection of ( d ) - the line which passes through M and perpendicular to A B and ( P , 3 ) .
The equation of ( d ) is 2 x − y + 2 3 = 0 The equation of ( P , 3 ) is x 2 + y 2 = 9
To get the result, we calculate the squared of the radius of ( O ) that is
r 2 = O B 2 = ( x O − 2 ) 2 + y O 2 = x O 2 + y O 2 − 4 x O + 4 = 1 3 − 4 x O
due to O is the intersection
We can calculate x O by substitute y O = 2 x O + 2 3 ) in x O 2 + y O 2 = 9 , solve it and choose x O < 0 (look at the figure)
We have
x O = 1 0 6 − 3 1 9
and thus
r 2 = 1 3 − 4 x O = 5 5 3 + 6 1 9
From the figure, we note that triangle AOB is isosceles such that AO=BO=x, where x is the radius of the circle.
∴ ∠OAP+∠PAB=∠ABO. Call ∠OAP α; ∠PAB β; and ∠ABO γ.
Our working inverse equation here is:
cos^(-1)α+cos^(-1)β=cos^(-1)γ
From this, we can obtain that cos(α+β)=cosγ Also, applying the cosine law and trigonometric identity leads us to the following relations: cosα=(x^2-8)/2x,cosβ=1/√5 ; sinα=(2√(-x^4+20x^2-64))/2x, sinβ=2/√5 ; cosγ=5/(2√5 x)
But cos(α+β)=cosγ is equivalent to cosα cosβ-sinα sinβ=cosγ Plugging in the values, (x^2-8)/2x∙1/√5- (√(-x^4+20x^2-64))/2x∙ 2/√5=5/(2√5 x) (x^2-8)/(2√5 x)- (2√(-x^4+20x^2-64))/(2√5 x)=5/(2√5 x) x^2-13=-2√(-x^4+20x^2-64)
Squaring both sides, we have x^4-26x+169=4(-x^4+20x^2-64) 5x^4-106x^2+425=0 Let m be equal to x^2 such that 5m^2-106m+425=0 Getting the roots of m by applying the quadratic formula, m=(106±√(106^2-4(5)(425)))/(2(5)) Simplifying, m=(53±6√19)/5. The area of the circle can be inferred to as mπ. Therefore, a=53,b=6,c=19,d=5, and a+b+c+d=53+6+19+5= 83
Let us solve this problem with Co-ordinate Geometry let point P(0,0) A(0,-1), B(2,0) Now join AB and get the midpoint C(1,-0.5) Equation of AB: x-2y=2 Let the perpendicular line to AB is MC Equation of MC: 4x+2y=3 Now consider a circle Z with centre at P, x^2+y^2=9 Now the top intersecting point of Circle Z and MC is ( (3 (2 - Sqrt(19))/10) , (3 (1 + 2 Sqrt(19) )/10) ) Hence the intersecting point is O as "the the perpendicular line to the midpoint of any arc of a circle always passes through the centre of the circle" now we know the point O and from the question we know A & B from here we get Radius of the circle so the term [{a+bsqrt(c)}/d] is simply the term R^2 when R^2 we get [{53+6sqrt(19)}/5] so a=53, b=6, c=19, d=5 and a+b+c+d= 83
I took P to be origin and solved the equations.it will require less effort
Denote circumscribed circle of triangle by CCT, circle with center 0, radius a by (O, a). CCT(PAB) x (O, 3) = {P, E} A B = 5 , P E = A B − 2 ( A P ∗ c o s ( P A B ) ) = A B − 2 ( 1 ∗ 5 1 ) = ( 5 ) − 2 ( 1 ∗ 1 / 5 ) = 3 / 5 O E = 3 2 − ( P E / 2 ) 2 = 9 − 9 / 2 0 = 3 ∗ 1 9 / 2 0 R = ( O E + 2 / 5 ) 2 + ( 5 / 2 ) 2 = ( 3 ∗ 1 9 / 2 0 + 2 / 5 ) 2 + ( 5 / 2 ) 2 R 2 = ( 3 ∗ 1 9 / 2 0 + 2 / 5 ) 2 + ( 5 / 2 ) 2 = ( 3 ∗ 1 9 + 4 ) 2 / 2 0 + 5 / 4 = 1 7 1 + 1 6 + 2 4 1 9 + 2 5 / 2 0 = ( 5 3 + 6 1 9 ) / 5 a + b + c + d = 8 3
Synthetic one (Without Trigonometry)
Suppose that P 1 and P 2 be points on lines A P and B P respectively such that ∠ O P 1 P = 9 0 ∘ and ∠ O P 2 P = 9 0 ∘ . Denote the lenght of O P 1 and O P 2 by x and y respectively and let the radii be r , then, by simple application of pytagorean theorem, we have O P 1 2 + O P 2 2 = x 2 + y 2 = O P 2 = 9 ⋯ ( 1 ) O A 2 = r 2 = O P 1 2 + P 1 A 2 = x 2 + ( 1 + y ) 2 = x 2 + y 2 + 2 y + 1 = 1 0 + 2 y ⋯ ( 2 ) O B 2 = r 2 = O P 2 2 + P 2 B 2 = y 2 + ( 2 + x ) 2 = x 2 + y 2 + 4 x + 4 = 1 3 + 4 x ⋯ ( 3 ) So, we get x = 4 r 2 − 1 3 and y = 2 r 2 − 1 0 . Now, substitute these into ( 1 ) : 4 r 4 − 2 0 r 2 + 1 0 0 + 1 6 r 4 − 2 6 r 2 + 1 6 9 = 9
After some manipulation, the equation turns into 5 r 4 − 1 0 6 r 2 + 4 2 5 = 0 ⟶ r 2 = 1 0 1 0 6 + 1 2 1 9 = 5 5 3 + 6 1 9 So, a + b + c + d = 5 3 + 6 + 1 9 + 5 = 8 3 .
Doing\quad it\quad with\quad co-ordinate\quad geometry\quad is\quad much\quad simpler.\ Take\quad O\quad as\quad origin\quad i.e.(0,0)\ P\quad as\quad (x,y)\ A\quad as\quad (x,y-1)\ B\quad as\quad (x+2,y)\ Given\quad PO\quad =\quad 3,\quad \ \dot { .\quad . } \quad { x }^{ 2 }+{ y }^{ 2 }=9\quad ...(1)\quad \quad \quad \quad \quad \quad \quad (Distance\quad formula)\ OA=OB\quad (Radius\quad of\quad the\quad circle)\ \dot { .\quad . } \sqrt { { x }^{ 2 }+{ (y-1) }^{ 2 } } =\sqrt { (x+2)^{ 2 }+{ y }^{ 2 } } \quad (Distance\quad formula)\ Squaring\quad both\quad sides\quad and\quad solving\quad further\quad we\quad get\ 4x+2y=-3\quad ...(2)\ Substituting\quad y=\frac { -3-4x }{ 2 } \quad in\quad (1)\quad we\quad get\quad a\quad quadratic\quad eq\quad in\quad terms\quad of\quad x\ i.e.\quad 20{ x }^{ 2 }+24x-27=0\ whose\quad roots\quad are\quad \frac { -6+3\sqrt { 19 } }{ 10 } \quad and\quad \frac { -6-3\sqrt { 19 } }{ 10 } .\ Discarding\quad the\quad second\quad root\quad since\quad x\quad needs\quad to\quad be\quad positive\quad as\quad it\quad lies\quad to\quad right\quad side\quad of\quad the\quad origin\quad O.\ Now\quad we\quad know\quad Radius\quad r\quad =\quad OB.\ { r }^{ 2 }\quad =\quad (x+2)^{ 2 }+{ y }^{ 2 }\ { r }^{ 2 }\quad =\quad { x }^{ 2 }+4x+4+{ y }^{ 2 }\ { r }^{ 2 }\quad =\quad 13+4x\quad \quad \quad \quad (Since\quad { x }^{ 2 }+{ y }^{ 2 }=9)\ Taking\quad x\quad as\quad \frac { -6+3\sqrt { 19 } }{ 10 } \ { r }^{ 2 }\quad =\quad \frac { 53+6\sqrt { 19 } }{ 5 } \ Clearly\quad a=53,\quad b=6,\quad c=19,\quad d=5\ \dot { .\quad . } \quad a+b+c+d\quad =\quad 83\
Is it correct
Fixed it?
D o i n g i t w i t h c o − o r d i n a t e g e o m e t r y i s m u c h s i m p l e r . T a k e O a s o r i g i n i . e . ( 0 , 0 ) P a s ( x , y ) A a s ( x , y − 1 ) B a s ( x + 2 , y ) G i v e n P O = 3 , . . ˙ x 2 + y 2 = 9 . . . ( 1 ) ( D i s t a n c e f o r m u l a ) O A = O B ( R a d i u s o f t h e c i r c l e ) . . ˙ x 2 + ( y − 1 ) 2 = ( x + 2 ) 2 + y 2 ( D i s t a n c e f o r m u l a ) S q u a r i n g b o t h s i d e s a n d s o l v i n g f u r t h e r w e g e t 4 x + 2 y = − 3 . . . ( 2 ) S u b s t i t u t i n g y = 2 − 3 − 4 x i n ( 1 ) w e g e t a q u a d r a t i c e q i n t e r m s o f x i . e . 2 0 x 2 + 2 4 x − 2 7 = 0 w h o s e r o o t s a r e 1 0 − 6 + 3 1 9 a n d 1 0 − 6 − 3 1 9 . D i s c a r d i n g t h e s e c o n d r o o t s i n c e x n e e d s t o b e p o s i t i v e a s i t l i e s t o r i g h t s i d e o f t h e o r i g i n O . N o w w e k n o w R a d i u s r = O B . r 2 = ( x + 2 ) 2 + y 2 r 2 = x 2 + 4 x + 4 + y 2 r 2 = 1 3 + 4 x ( S i n c e x 2 + y 2 = 9 ) T a k i n g x a s 1 0 − 6 + 3 1 9 r 2 = 5 5 3 + 6 1 9 C l e a r l y a = 5 3 , b = 6 , c = 1 9 , d = 5 . . ˙ a + b + c + d = 8 3
Log in to reply
If you use O as (0,0) & denote h as the height Tr. OAB and let P be (x,y) then: x²+y²=1 and (x-√ 5)²+y²=4 which gives x=1/√ 5, y=2/√ 5 the other root being inadmissible. Further, (2/√5 -h)²+(1/√5 -√5/2)²=9 while area of the circle = Pi*(h²+5/4) = (53+6√19)Pi/5.
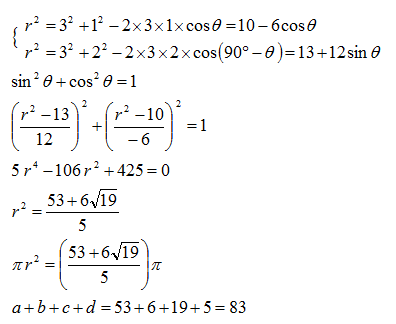
Let A O = O B = r . Also, let ∠ A P O = α .
By Law of Cosines on △ A P O , we have r 2 = 1 2 + 3 2 − 2 ⋅ 1 ⋅ 3 ⋅ cos α
Now note that ∠ B P O = 2 7 0 − α
By Law of Cosines on △ B P O , we have r 2 = 2 2 + 3 2 − 2 ⋅ 2 ⋅ 3 ⋅ cos ( 2 7 0 − α ) .
Observe that cos ( 2 7 0 − α ) = − sin α (draw it on the unit circle if you are not convinced).
Therefore, r 2 = 2 2 + 3 2 + 2 ⋅ 2 ⋅ 3 ⋅ sin ( α )
Simplify, and we have a system of equations: { r 2 = 1 0 − 6 cos α r 2 = 1 3 + 1 2 sin α
Setting the two equations equal: 1 0 − 6 cos α = 1 3 + 1 2 sin α
We want to work with either only cos α or only sin α , which makes us think of sin 2 α + cos 2 α = 1 . Thus, we aim to square both sides of the equation.
Isolating the sin α : 1 2 sin α = − 3 − 6 cos α
Dividing by 3 and squaring: 1 6 sin 2 α = 1 + 4 cos α + 4 cos 2 α
Using sin 2 α = 1 − cos 2 α : 1 6 − 1 6 cos 2 α = 1 + 4 cos α + 4 cos 2 α
Rearranging: 2 0 cos 2 α + 4 cos α − 1 5 = 0
Aha, a quadratic! Let's let cos α = x for now. 2 0 x 2 + 4 x − 1 5 = 0
Solving using the quadratic equation, we get that x = 1 0 − 1 ± 2 1 9
But which one is the correct value of x ? We know that there can only be a unique α , but there are two possible values of x .
Let's observe that type of angle α is. α seems to be an obtuse angle. Therefore, cos α < 0 , and the value we want is x = 1 0 − 1 − 2 1 9 .
So now we know that cos α = 1 0 − 1 − 2 1 9 . Looking back at what we want to find, we see that we want to find π r 2 . We already have an equation for r 2 though: r 2 = 1 0 − 6 cos α
Plugging in cos α = 1 0 − 1 − 2 1 9 gives r 2 = 1 0 − 6 ( 1 0 − 1 − 2 1 9 ) = 5 5 3 + 6 1 9 .
Thus, the area of the circle is ( 5 5 3 + 6 1 9 ) π . Clearly, a = 5 3 b = 6 c = 1 9 d = 5
Therefore, our answer is finally 5 3 + 6 + 1 9 + 5 = 8 3 and we are finally done! □
Problem maker's note: This particular problem took me roughly 1.5 hours , the longest I have ever taken, from idea to finished product, so if you like it, please show your support!