This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
14 solutions
genius solution - indeed
Log in to reply
Log in to reply
but i can give a more genius solution : Consider the above representation of the problem. The red lines connect the center of the circle to the vertices of the triangle. Notice that by circle theorems, they bisect the coloured regions, split by the radius of the triangle, into two congruent parts. then we have ; tan a = 4/x , tan b = 4/8 , tan c = 4/6
As angles in a triangle add to 180 degrees: we have 2a + 2b + 2c = 180 , then a+b + c = 90 , b+c = 90-a from above : tan (b+c) = (2/3+1/2) / ( 1 - 2/3*1/2) = 7/4 = cot a = x/4 , there fore x = 7
amazing solution !
Me toooo in d same way
even i did in same process
it should be 14+x in the third last steps and other steps to follow.
iam use arctan and arcsine but thise need time
Same Solution
Did the same way too
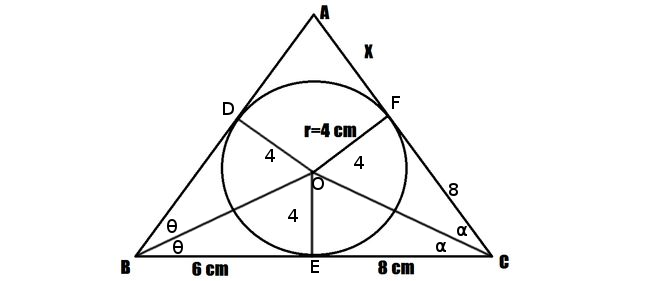 tan θ = 4/6 = 2/3
tan θ = 4/6 = 2/3
tan 2θ = 2(2/3)/(1-(2/3)^2)=12/5
implies sin 2θ = 12/13 and cos 2θ = 5/13
tan α = 4/8 = 1/2
tan 2α = 2(1/2)/(1-(1/2)^2)=4/3
implies sin 2α = 4/5 and cos 2α = 3/5
sin ∠BAC = sin (180-(2α+2θ))
=sin(2α+2θ)
=sin(2α)cos(2θ)+cos(2α)sin(2θ)
=(4/5)(5/13)+(3/5)(12/13)
=56/65
Using sine theorem:
(x+8)/sin 2θ=(6+8)/sin ∠BAC
(x+8)/(12/13)=14/(56/65)
=> x=7
Proof of my assumptions :
In triangle BDO and BEO,
DO=OE=radius=4
∠BDO=∠BEO=90° (Tangents to the circle)
BO is common in both triangles.
Therefore, triangle BDO and BEO are congruent. (RHS)
So, we can say ∠DBO=OBE=θ.
Similarly, triangle CEO and COF are congruent.
nice solution sir. i too have posted my solution with a different approach, have a look at it...
very similar to my method Illuminati confirmed....
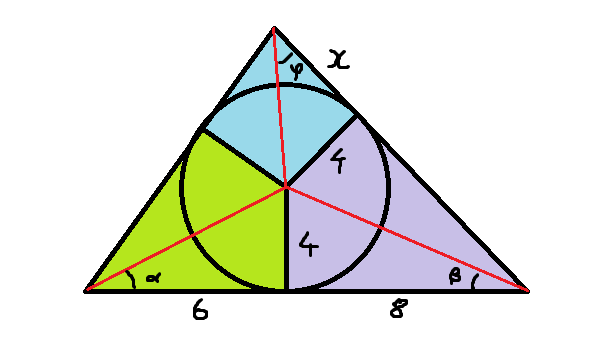
Consider the above representation of the problem. The red lines connect the center of the circle to the vertices of the triangle. Notice that by circle theorems, they bisect the coloured regions, split by the radius of the triangle, into two congruent parts.
By trigonometric functions: tan α = 4 / 6 tan β = 4 / 8 tan γ = 4 / x As angles in a triangle add to 180 degrees: 2 α + 2 β + 2 γ = 1 8 0 arctan 4 / 6 + arctan 4 / 8 + arctan 4 / x = 9 0 tan ( arctan 4 / 6 + arctan 4 / 8 + arctan 4 / x ) = u d f ( * )
I'll now use the identity tan ( a + b + c ) = 1 − tan a tan b − tan b tan c − tan c tan a tan a + tan b + tan c − tan a tan b tan c We can plug in the numbers into this identity but if we first notice that since the right hand side of (*) was undefined, the denominator of the identity must be zero so therefore 1 − tan ( arctan 4 / 6 ) tan ( arctan 4 / 8 ) − tan ( arctan 4 / 8 ) tan ( arctan 4 / x ) − tan ( arctan 4 / x ) tan ( arctan 4 / 6 ) = 0 1 = 4 / 6 ∗ 4 / 8 + 4 / 8 ∗ 4 / x + 4 / x ∗ 4 / 6 1 = 1 / 3 + 2 / x + 8 / 3 x 2 / 3 = 6 / 3 x + 8 / 3 x 2 = 1 4 / x x = 7
nice solution sir. i too have posted my solution with a different approach, have a look at it...
tan(B/2)=4/6=2/3
tanB=2tan(B/2)/(1-tan²B/2)=12/5
tan(C/2)=4/8=1/2
tanC=4/3
A+B+C=180°
tan(B+C)=tan(180°-A)=-56/33=-tanA
tan(A/2)=4/x
tanA=(8/x)(1-16/x²)=56/33
7x²-33x-112=0
x=7
nice solution sir. i too have posted my solution with a different approach, have a look at it...
The semi perimeter of the triangle is (14+x). We know ,inradius of circle inscribed in a triangle = area of triangle / semi perimeter i.e. r = area /s ........(1). Here , r= 4 , area by heroin's formula is sq rt s(s-a).(s-b).(s-c) Substituting the values in (1) and squaring nd solving we get x= 7
Nice approach. Just sayin' , what do you mean by "inradius of circle inscribed in a triangle" ??? I mean, go on read that again. Sense something?? And "heroin's formula". Seriously. You rock.
Since the sides of △ABC are tangents of the incircle, the lengths of AB, BC, CA are x+6, 14, and x+8 respectively.
So when we apply the cosine rule, we can get an equation:
(x+8)^2 = (x+6)^2 + 14^2– 2(x+6) 14 cos ∠ABC
Now note that ∠ABC = ∠ABO + ∠OBC when O is the center of incircle.
And ∠ABO = ∠OBC because tan ∠ABO = tan ∠OBC = r/6 = 4/6
So cos ∠ABC = cos 2(∠OBC )
= cos2 ∠OBC - sin2 ∠OBC = (36-16)/52 = 5/13
No plug in for cos ∠ABC = 5/13, we’ll solve for x:
(x+8)^2 = (x+6)^2 + 14^2– 2(x+6) 14 (5/13)
X2+ 16x +64 = X2+ 12x +36 + 196 – (140/13)(x+6)
(140/13)(x) + (140*6/13) = 168 – 4x
(192/13)(x) = 168 - (140*6/13)
192x = 13 (168) - (140) 6 = 1,344
X = 7
use the fact that area of the triangle can be found out by heron's formula as well adding the area of 3 triangles which comprises the whole triangle each having the height 4cm and bases as 14cm, (x+8)cm, (x+6)cm. thus equating the area of triangle ABC found in 2 methods we have : {(14+x) (x) (6) (8)}^(1/2) = ½{(4) (14) + (4 (8+x)) + (4 (6+x))} solving this equation we get the equation {(x^2) +7x-98} = 0 solving it we get x = 7.
Why have you taken two sides as x+8. And x+6. Plz tell
Log in to reply
As length of the 2 tangents drawn from the same point are equal...
see the above figure one side is 14cm and the side which is connected to the side having side as 8cm is (x+8) cm and the other is similarly (x+6) cm
Project a perpendicular line from center of the circle to member BC it will intersect with the tangent point call it Z ,,call the tangent point with member AC `N' & center of the circle 'M' ∆ czm is right angle so mc=√16+64=4√5, Angle {mcz}={mcn}=P so cos{P}=8/4√5=2÷√5 , Angle ACB=2p=U so cos{U}=2×{4÷5}-1=(3÷5). By using the law of cosin, cos(U)=3÷5=14^2+(8+X)^2-(6+X)^2/(2×14×(8+X) So 3×28×(8+X)=5×(196+64-36+4X) so 64X=448,,, X=7########
OE⊥AC,and assume the extended center lind AO⊥BC at D,then △ADC≌△AEO.we use te Pythagoras theorem can estimates the X about 7.5,so the answer is 7 or 8,so,if the X=8,must have BE⊥BC,but they don`t,so the answer must is 7
I had solve it by using the law of sines
Isn't this class 10 ncert maths?
I kind of brute forced it by using x in equations. I found the area of the triangle with Heron's Formula and used the product of the inradius and semiperimeter to get the area again. This gave me: sqrt((x+14)(x)(6)(8))=56+4x 48(x+14)(x) = 16(x+14)^2 3x = x+14 2x = 14 x = 7 I then solved this to get one real solution, x = 7.
Consider the well-known 13-14-15 triangle. Note that its inradius is well-known to be 4. Since B C = 1 4 , it follows that 1 5 = 8 + x (or 1 3 = 6 + x ) thus x = 7 .
It's not that well known
Log in to reply
Yes it is well known. In fact, if you do enough competitions, you should know for fact that the area is 84 and the innards is 4 and the circumradius is 8 1/8. If you didn't know, you could solve this problem easily enough with heron's and A=rs.
2 MINUTES IN ACAD
Area of the triangle made of the vertices B,C and incentre= 1/2x4x(6+8)=28. therefore area of the triangle ABC (delta)= 3*28= 84. As we know that, r=delta/s. now s=((6+8)+(8+x)+(x+6))/2=14+x. Delta=84, r=4 Therefore, s=14+x=84/4=21. so, x=7.
How did u come to the result that area of triangle ABC is 3*28? How can we say that area of triangle ABC is thrice the area of triangle made by vertices B & C & incentre.
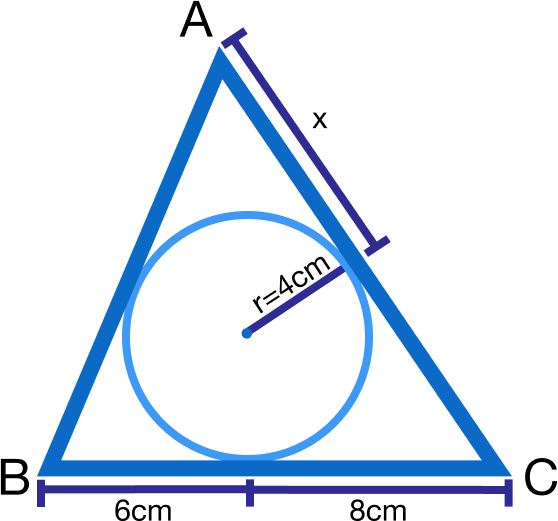
I n r a d i u s ( r ) o f a t r i a n g l e = s Δ w h e r e Δ = a r e a o f t h e t r i a n g l e a n d ( s ) i s s e m i p e r i m e t e r
⇒ r = s s ( s − a ) ( s − b ) ( s − c )
⇒ r = s ( s − a ) ( s − b ) ( s − c )
w h e r e a = 6 + 8 = 1 4 , b = x + 8 a n d c = 6 + x
A n d G i v e n t h a t i n r a d i u s o f t h e g i v e n t r i a n g l e ( r ) = 4 c m
⇒ 4 = 1 4 + x ( 1 4 + x − 1 4 ) ( 1 4 + x − ( 8 + x ) ) ( 1 4 + x ( 6 + x ) )
⇒ 1 6 = 1 4 − x ( x ) ( 6 ) ( 8 )
⇒ 2 2 4 − 1 6 x = 4 8 x
∴ x = 3 2 2 2 4 = 7