It's beautiful
3 Circles of radius 10 are tangent to each other and to a plane in 3 dimensional space. Each of the circles is inclined at 4 5 ∘ to the plane. There are 3 points where the circles touch each other. These 3 points lie on a circle parallel to the plane. The radius of this circle is A , evaluate ⌊ 1 0 A ⌋ .
The answer is 73.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Wouldn't it be 10 cos pi/4?
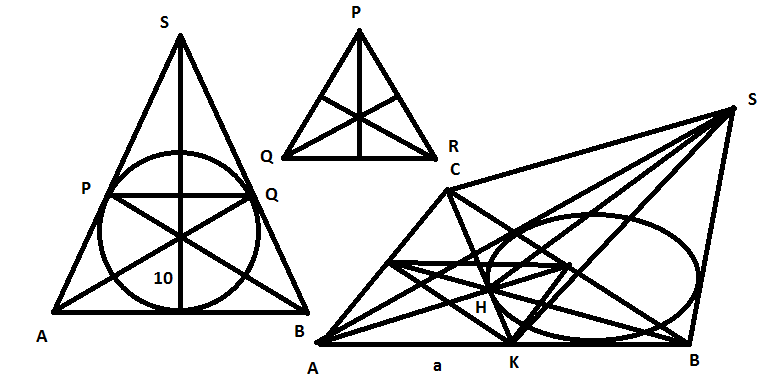 It is easy to realize that three circles are in-circles of three triangles. These triangles are three faces of the pyramid as in the diagram.
H
K
=
a
∗
6
3
∠
S
K
H
=
4
5
0
S
A
=
4
a
2
+
6
a
2
=
a
1
2
5
r
(
a
+
2
a
1
2
5
)
=
a
∗
6
a
a
=
1
0
∗
(
6
∗
(
1
+
2
∗
1
2
5
)
)
S
A
=
1
0
∗
(
6
∗
(
1
+
2
∗
1
2
5
)
)
∗
1
2
5
a
P
Q
=
S
A
S
A
−
2
a
A
=
R
P
Q
R
=
3
P
Q
=
7
.
3
[
1
0
A
]
=
7
3
It is easy to realize that three circles are in-circles of three triangles. These triangles are three faces of the pyramid as in the diagram.
H
K
=
a
∗
6
3
∠
S
K
H
=
4
5
0
S
A
=
4
a
2
+
6
a
2
=
a
1
2
5
r
(
a
+
2
a
1
2
5
)
=
a
∗
6
a
a
=
1
0
∗
(
6
∗
(
1
+
2
∗
1
2
5
)
)
S
A
=
1
0
∗
(
6
∗
(
1
+
2
∗
1
2
5
)
)
∗
1
2
5
a
P
Q
=
S
A
S
A
−
2
a
A
=
R
P
Q
R
=
3
P
Q
=
7
.
3
[
1
0
A
]
=
7
3
The given plane is the O x z plane, and the circles are placed symmetrically around the origin. One of the circles has its center at x = 0 . The coordinates of this center are ( 0 , r / 2 , c ) , where c is yet to be determined.
The points on this circle may be parametrized as ( x , y , z ) = ( r cos θ , 2 r ( 1 − sin θ ) , c − 2 r sin θ ) . The direction of the tangent to the circle at each point is ( d x , d y , d z ) ∝ ( − sin θ , 2 cos θ , 2 − cos θ ) .
Because of symmetry, we expect this circle to touch neighboring circles in the planes x / z = ± tan 6 0 ∘ = ± 3 . The tangent vectors at the point of contact must also lie in this plane, d x / d z = ± 3 . We focus on the positive side. This gives the equations 3 = z x = c − ( r 2 ) sin θ r cos θ ∴ c − 2 r sin θ = 3 r cos θ , 3 = d z d x = − ( cos θ ) / 2 − sin θ ∴ cos θ sin θ = 2 3 . Thus we find θ = inv tan 2 3 ≈ 5 0 . 7 7 ∘ ; sin θ = 5 3 , cos θ = 5 2 . The coordinates of the points where the circles touch are ( x , y , z ) = ( r cos θ , 2 r ( 1 − sin θ ) , 3 r cos θ ) = r ( 5 2 , 2 1 − 1 0 3 , 1 5 2 ) . Finally, the radius of the circle through the touching points is A = x 2 + z 2 = r 5 2 + 1 5 2 = r 1 5 8 ≈ 0 . 7 3 0 3 r . Substituting r = 1 0 we get ⌊ 1 0 A ⌋ = 7 3 .
The three circumferences are inscribed into three triangles, in particular let's consider three triangles such that they define a tetrahedron whose faces are inclined of 45° respect the base plane.
Let's call AOB one of this three triangles who contains the three circles.
Be h the tetrahedron's height.
Being the circumferences incliend of 45° the height of the triangle AOB results to be h*sqrt(2).
I've preferred handwrite the solution
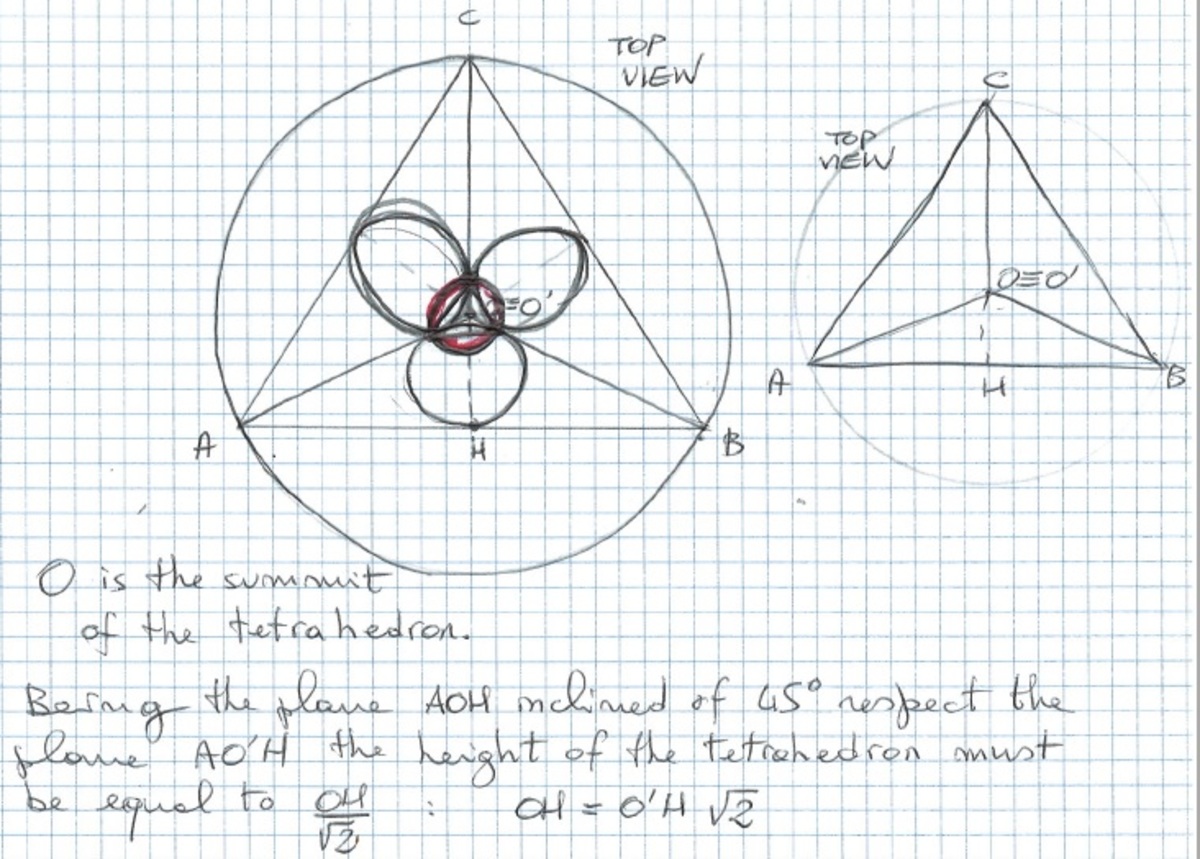
 .
.
The projection of the three circles on the plane would be three ellipses.The vertical semi axis will be contracted to The projection of the three circles on the plane would be three ellipses. The vertical semi axis will be contracted to 1 0 C o s 4 5 = 2 1 0 . E l l i p s e 1 E l l i p s e 1 is along X-axis with center at (0,0). Its equation is 2 X 2 + ( ± Y ) 2 = 1 0 0 . S l o p e o f o n e o f i t s t a n g e n t S T 3 , i s m 3 = d x d y . : − W h e r e 4 X + ( − Y ) d x d y = 0 , m 3 = d x d y = Y 2 X . Since 3 circles are placed symmetric w.r.t. vertical line of symmetry through S, tangent lines S T 2 , S T 3 , o f E l l i p s e 1 would be at an angle of 360/3=120. ∴ S l o p e o f S T 3 , i s m 3 = T a n ( 2 1 2 0 ) = 3 . B u t m 3 = Y 2 X a l s o . ∴ X = − 2 3 ∗ Y . Putting this X value of point of tangency T 3 i n e q u a t i o n f o r E l l i p s e 1 , 2 ∗ ( 2 3 ∗ Y ) 2 + Y 2 = 1 0 0 , a n d s o l v i n g w e g e t Y = 2 1 0 . ∴ T 2 T 3 = 2 ∗ Y = 4 1 0 . A l l t h r e e E l l i p s e s For the 3 ellipses, these three lines joining 2 points of tangency of an ellipse, form an equilateral triangle T 1 T 2 T 3 . The circumcircle of this triangle passes through the three points of tangency. ∴ S T 1 = R = 3 4 1 0 = 7 . 3 0 = A ∴ ⌊ 1 0 A ⌋ = 7 3
Let the plane that the circles are inclined to be the xy-plane. Circles of radius 1 0 are then projected to ellipses of semi-major axis length 1 0 and semi-minor axis length 5 2 . Set the origin to be the center of symmetry of this setup. Suppose one of these ellipses in centered at ( a , 0 ) . By symmetry, this ellipse should be tangent to the lines y = ± tan ( 6 0 ∘ ) x = ± 3 x . The ellipse can be described by the parametric equations x = a + 5 2 cos t , y = 1 0 sin t . It follows that the gradient of the tangent to a point ( x , y ) is d x d y = d t d x d t d y = − 5 0 sin t 1 0 0 cos t = − y 2 ( x − a ) . It is expected that if y = 3 x is substituted to this expression, the gradient value should be 3 : 3 = d x d y = − 3 x 2 ( x − a ) ⇒ 3 x = 2 ( a − x ) ⇒ x = 5 2 a ⇒ y = 5 2 a 3 . Substituting these values into the ellipse equation 2 ( x − a ) 2 + y 2 = 1 0 0 and solving for a gives us a = 5 3 1 0 (the negative solution gives a symmetric case. So the radius of the circle is simply A = cos ( 3 0 ∘ ) y , leading to ⌊ 1 0 A ⌋ = ⌊ 5 4 0 a ⌋ = 7 3 .
Consider the top view of the setup. The projection of a circle will be an ellipse. Since the circles are tilted at pi/4 the semi major axis will remain 10 while the semi minor axis will be 10 tan pi/4. now we have three ellipses tangent to each other and a circle passing through them as shown..jpeg?width=1200)
notice that the slope of the drawn tangent is tan pi/6. Using some basic trigonometry and calculus we can find the side of the triangle and hence the radius of the circle, which comes out to be 1 6 0 / 3