An algebra problem by A Former Brilliant Member
Find the minimum value of a a b b c c , where a , b , and c are positive real numbers such that a + b + c = 1 .
The answer is 0.333.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Elegant and compact solution.
Just enclose your formulas with "\ (" and "\ )" (without spaces between backslash "\" and brackets "()") to effect the LaTex code.
Log in to reply
I'm too lazy to use LaTex at this age :D
Log in to reply
I am 61. You need only 6 more keystrokes. I amended your problem I added 12 keystrokes for Latex. I have rephrased it to read better. It is unnatural to start a sentence in lowercase.
Which sentence? If it was so, I'm very sorry for that typing error.
Log in to reply
You original problem starts with "a, b, c are positive integers...".
Because of symmetry, a==b==c, Using the constraint a+b+c=1 and replacing b and c with a gives 3a=1 or a = 3 1 . Evaluating a a b b c c as 3 1 1 gives the minimum as 3 1 .
Your premise is not always correct. See this article .
After reviewing the article and concluding the argument had sufficient validity to warrant a reworking of this problem from the start, I did just that.
I plotted
a
a
between 0 and 1:
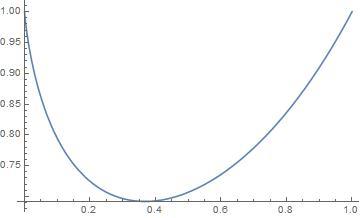
To find the minimum of a a , ∂ a ∂ a a ⇒ a a ( lo g ( a ) + 1 ) which, since the function is concave upwards, means that the minimum is at e 1 .
This can be used as an estimate of where the minimum is. The minimum can not be there exactly as e 3 > 1 .
I plotted the expression in an appropriate range, noting that because if the
a
+
b
+
c
=
1
constraint, the valid region will be triangular by the origin:
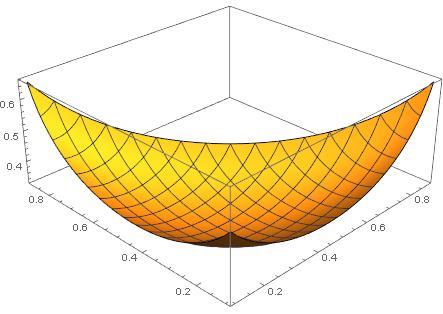
This supports my original solution.
Let us see what Wolfram Mathematica 12 has to say, Assuming [ ( a ∣ b ) ∈ R , Minimize [ { a a b b ( 1 − ( a + b ) ) 1 − ( a + b ) , 1 0 2 ≤ a ≤ 1 0 4 ∧ 1 0 2 ≤ b ≤ 1 0 4 } , { a , b } ] ] ⇒ { 3 1 , { a → 3 1 , b → 3 1 } }
Vindicated.
We note that f ( x ) = x ln x is convex. Hence by Jensen's inequality , we have:
3 a ln a + b ln b + c ln c a ln a + b ln b + c ln c ⟹ a a b b c c ≥ 3 a + b + c ln ( 3 a + b + c ) ≥ − 3 ln 3 ≥ − ln 3 ≥ 3 1 ≈ 0 . 3 3 3 And equality occurs when a = b = c = 3 1