It's easy if you know!

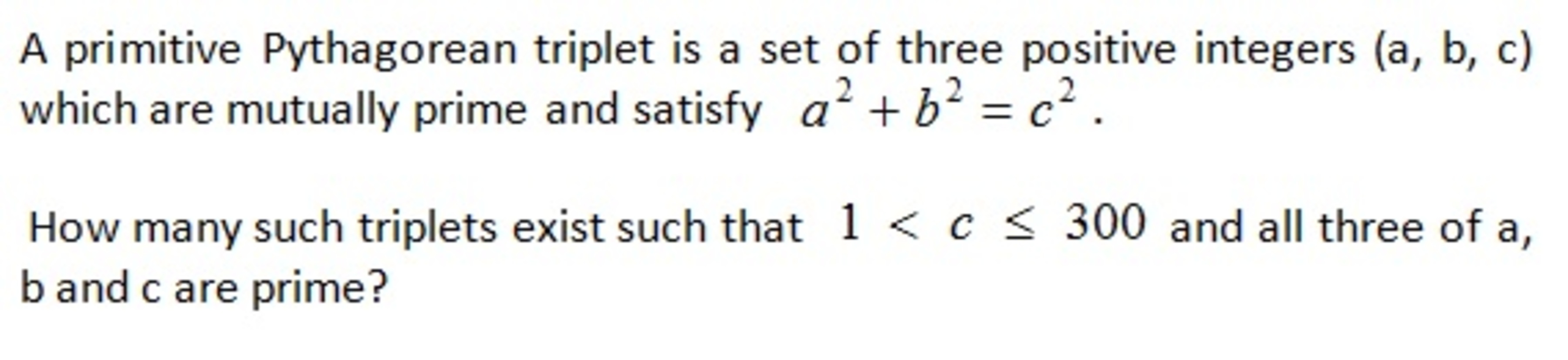
Mod 4, any square is either 0 (if the number is even) or 1 (if the number is odd). Then if $a^2+b^2=c^2$ ( $a,b,c$ all prime), exactly one or three of them must be even for the equation to hold modulo 4. That is, one or three of the primes is 2. Moreover, $c>a,b$ , so $c\neq 2$ .

Assume $a=2$ , $b,c$ are odd. Then $c^2=b^2+4$ . But $c>b$ , and since $b,c$ are odd, $c<b+1$ . Then $c^2\ge (b+2)^2=b^2+4b+4$ . Thus, $b^2+4\ge b^2+4b+4$ , implying $b\le 0$ and contradicting $b$ being prime.

Thus, there are no Pythagorean triplets consisting of three prime numbers, so the answer is $\boxed{0}$ (regardless of the given range for $c$ ).

Primitive Pythagorean triples satisfy the following conditions: $\ (a,b,c) = (2xy, \ ~ \ x^2 -y^2, \ ~ \ x^2 +y^2) \ ~ \forall y > x > 0$ $\ from \ (2xy)^2 +(x^2 -y^2)^2 = (x^2 +y^2)^2$ Now clearly $\ 2xy$ is even so at least one of a and b are even and hence not prime. Also, note that $\ 2xy = 2 \implies x=y = 1$ but this contradicts x < y and the fact that they are coprime natural numbers.