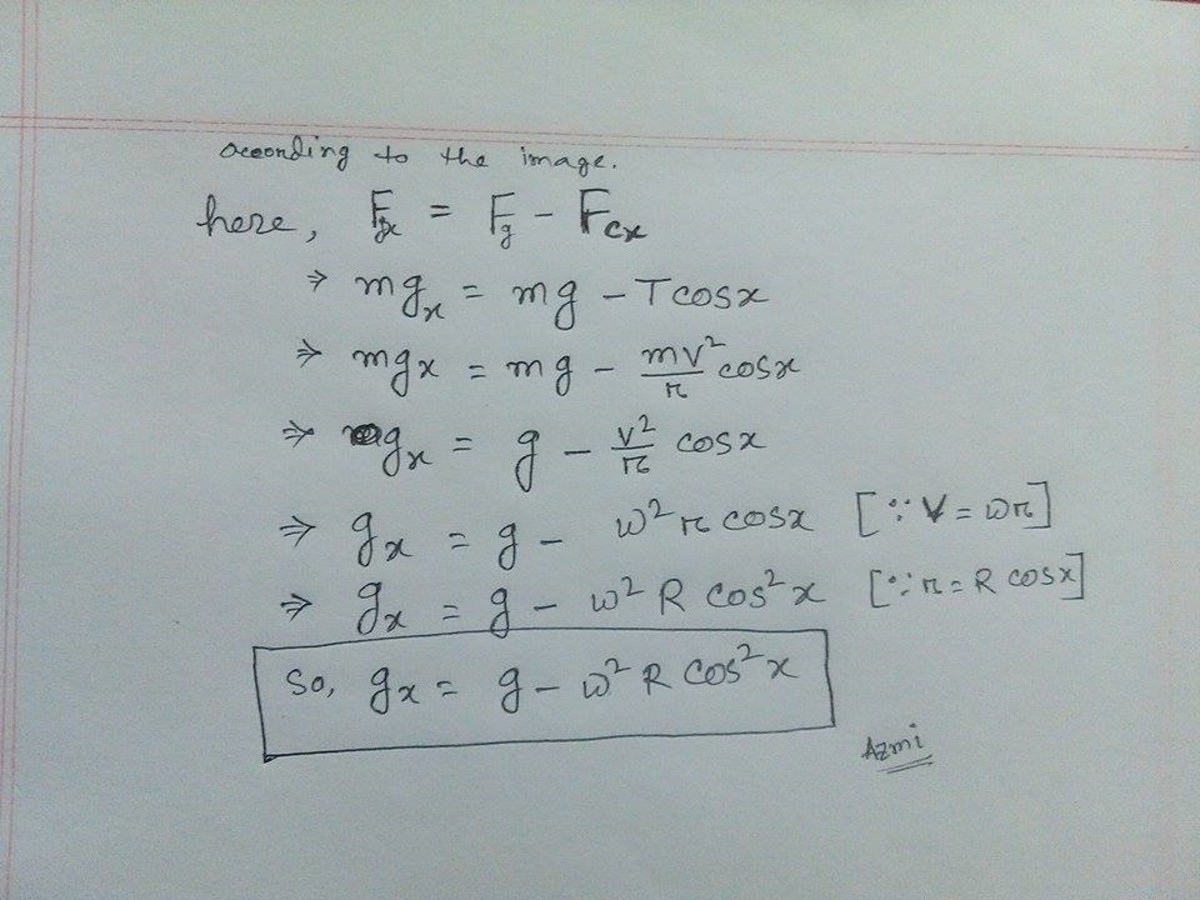Gravity Effectively Isn't Constant

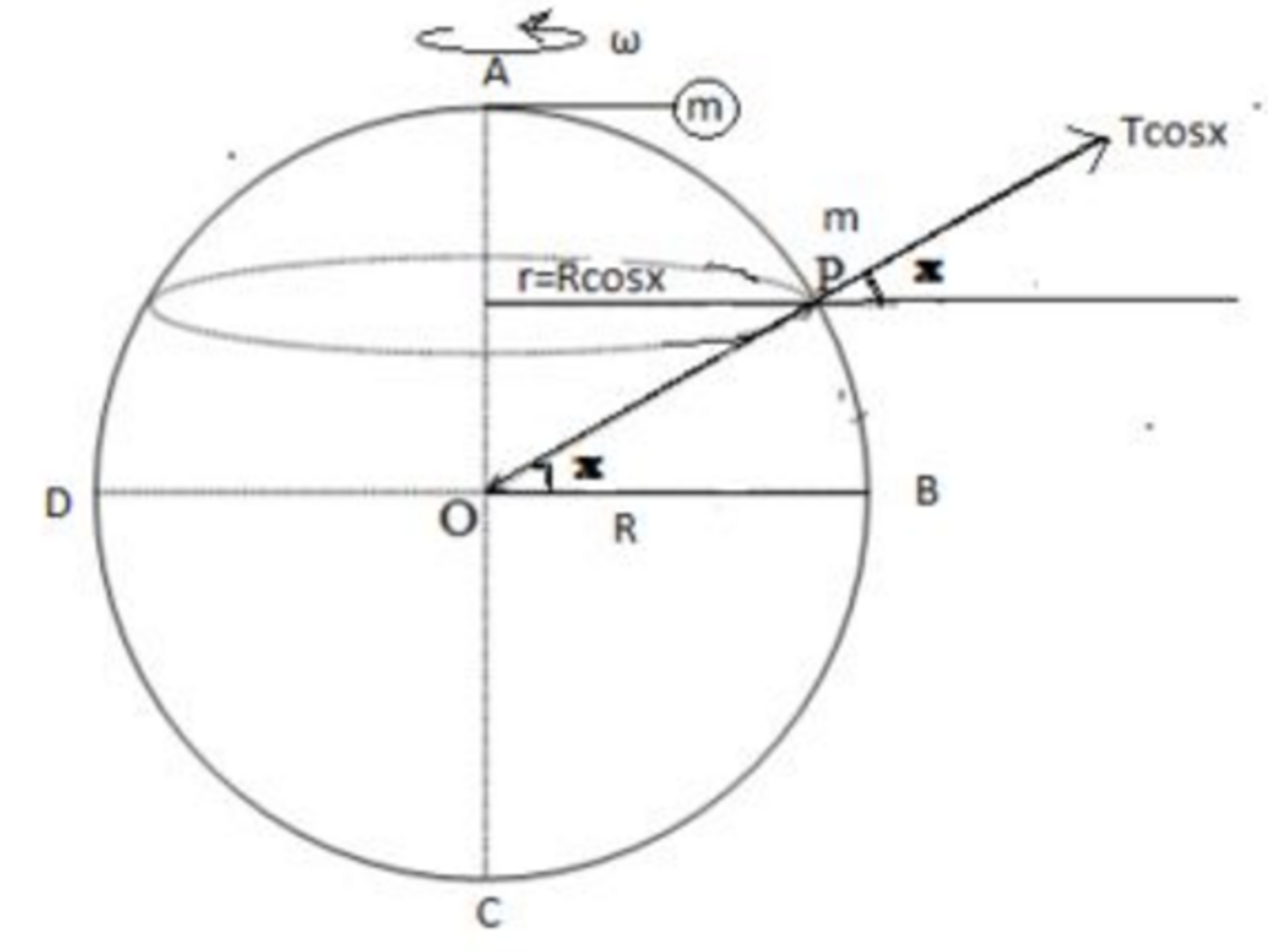
Consider a spherical planet with radius $R$ , that is rotating with angular velocity $\omega$ about it's axis. The lattitude $x$ of a point $P$ that is a height of $h$ away from the equator, is denoted as $x = \frac{h}{R}$ . Suppose that the acceleration due to gravity at the North pole is $g$ , then what is the effective acceleration ar point $P$ in terms of the latitude $x$ ?

• $T \cos x$ is the Centrifugal force along the tangent for rotation.