It's Green
The distance between any two adjacent cars at a red light is 2 meters.
As soon as the light turns green, the first car starts accelerating at 4 m / s 2 . As soon as the first car reaches a speed of 6 m / s , the second car starts accelerating at the same rate. In exactly the same fashion, each successive car starts accelerating when the car in front of it reaches 6 m / s , and accelerates at 4 m / s 2 until it reaches the speed 2 0 m / s .
When all cars have reached the same speed 2 0 m / s , how far apart are two adjacent cars (in meters)?
The answer is 32.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
13 solutions
@Arjen Vreugdenhil nice solution.
Its so nice that we get 3 tries on numerical solutions. Same reasoning but first try 30. No!? What did I overlook? Ah the 2m extra. Thanks.
Log in to reply
I forgot it too and still was wondering.... What? Until I read discussion haha. Than I was like... You fool!
How did you get 1.5s?
Log in to reply
Because you are accelerating to a velocity of 6 m/s at rate of 4m/s^2, which takes approx. one and a half seconds. So it takes the first car in line 1.5 seconds to get to the speed at which the next car in line is allowed to start accelerating.
What are the make and models of the cars? are the same? are the weights and loads the same? This question is moot.
X2 = 43.5 m at t = 6.5 s ( " X2(t) = 2t² - 6t - 2 " / " V2(t) = 4t - 6 " ) ( V2(1.5s) = 0 m/s and X2 ( 1.5) = -2 m ) What did I do wrong ?
Log in to reply
2 ⋅ ( 1 . 5 ) 2 − 6 ⋅ 1 . 5 − 2 = − 6 . 5 , not − 2 .
The correct equation would be x 2 ( t ) = 2 t 2 − 6 t + 2 . 5 , so that x 2 ( 6 . 5 ) = 2 ⋅ ( 6 . 5 ) 2 − 6 ⋅ 6 . 5 + 2 . 5 = 4 8 .
for all I know the first car can be reaching the 6m/s for the next 20 years...
If the acceleration is 4m/sec^2, then the rate of acceleration is equal to 4t. the velocity at a time t would be 2t^2. The point where the first car reaches 6m/s would be where 6=2t^2, or 3^.5. this would give a distance at the terminal speed of 20m/s of approx 36.6 meters. the answer is not an integer, or 36 or 37 should be accepted. Or is acceleration really linear?
Log in to reply
The velocity at time t would be equal to v = 4 t .
The position at time t would be equal to x = 2 t 2 .
The car reaches a velocity of 6 m/s when 6 = 4 t , or t = 1 . 5 . Your calculation 6 = 2 t 2 determines when the car reaches position 6 m.
Here is a graphical illustration of Arjen's solution. The green curve is identical to the red curve, but shifted by 1.5s and 2m.
Great graphic but you make a mistake you put the 1.5 between the sec. 5.5 and 7 but the case occurs in seconds 5 and 6.5 ✌
Log in to reply
It does not matter where I put the arrow on the graph. The displacement along the time axis between the two graphs is always 1.5s, independent of what time you are looking at.
It's easier to see from the velocity time graph. You just calculate the difference between the distance travelled by successive cars, which is the area of the repeating parallelograms =)
Log in to reply
Agreed. I drew a v,t graph myself and from there it is simple multiplication and super-intuitive. This graph is too complicated for the task... If the problem would have stated that the second car started driving when the distance was a certain amount, then this x,t graph makes more sense.
Log in to reply
Agree! Just evaluate 1.5*20=30 for the parallelogram area, +2 for the initial distance. Total distance 32m.
If the acceleration is 4m/sec^2, then the rate of acceleration is equal to 4t. the velocity at a time t would be 2t^2. The point where the first car reaches 6m/s would be where 6=2t^2, or 3^.5. this would give a distance at the terminal speed of 20m/s of approx 36.6 meters. the answer is not an integer, or 36 or 37 should be accepted. Or is acceleration really linear?
Log in to reply
Your formula for the velocity is incorrect. The velocity at time t is v = a t = ( 4 m / s 2 ) t , therefore t = v / a = 4 m / s 2 6 m / s = 1 . 5 s .
Each car starts moving 1 . 5 s after the car in front. The distance travelled & time taken during acceleration is the same for every car, but the car in front will have travelled at 2 0 m/s for 1 . 5 s before the car behind reaches top speed. This means the car in front will have travelled 3 0 m more than the car behind. adding this to the starting 2 m gap gives us the total difference of 3 2 m .
There is a problem with the answer. The problem states that distance apart is when all car reach 20m/s. Therefore the first car stops accelerating once it reaches 20m/s yet the second car continues to accelerate until it reaches 2m/s. Therefore the two cars are accelerating for the same period at the same acceration covering the same distance. The answer is 2m
Log in to reply
That would be the case if they started accelerating at the same time, but they didn't. The car behind is at 0m/s for 1.5 seconds longer than the car in front (before accelerating), and the car in front is at 20m/s for 1.5 seconds longer than the car behind (after accelerating).
Consider the graph of speed as a function of time. At this rate of acceleration, each car starts accelerating 1.5 s after the one before. The colors of the lines are the same as the cars in the problem. Therefore the blue area is the distance between the blue and the red car, if they had started together, so 30 m. As they started 2 m apart, they end up being 32 m apart.
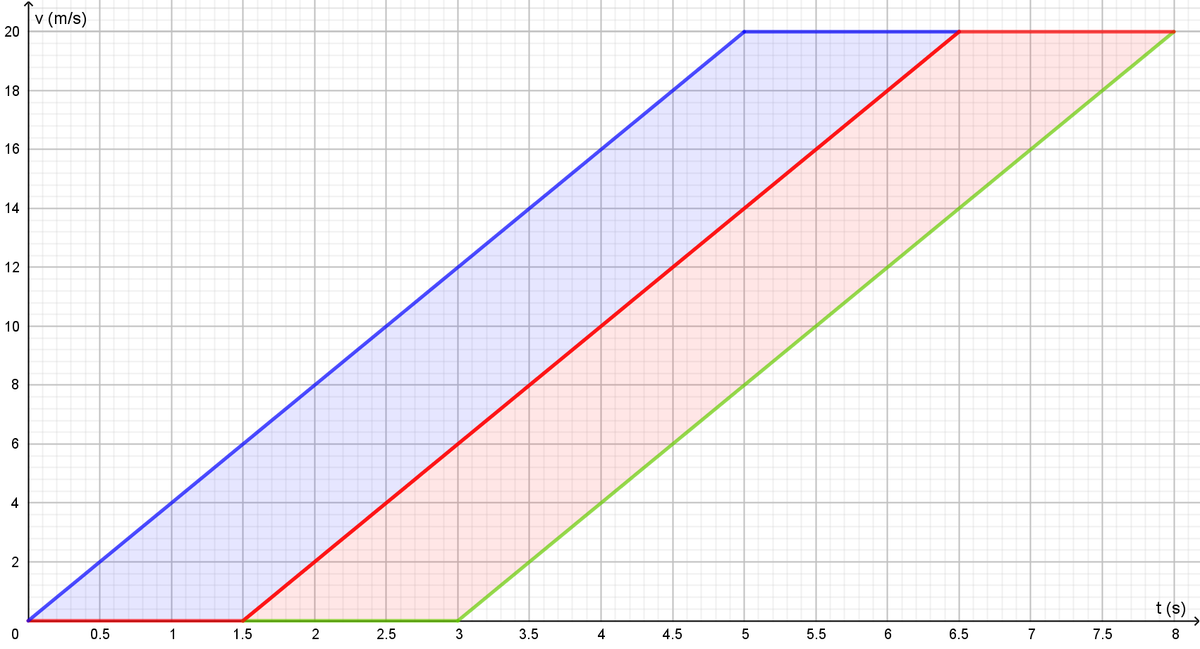
And, essential to your solution: the blue area (the part between the blue and red graph) is equal to the difference in displacement of the two cars. It is a parallelogram with base 1 . 5 s and height 2 0 m / s .
Ignore the acceleration, the cars do the same thing just offset by 1.5 seconds. When travelling at 20 m/s, 1.5 seconds translates to a 30 meter difference. They were also 2 meter apart at the start giving 2 0 m / s × 1 . 5 s + 2 m = 3 2 m
How did you get 1.5 seconds?
Log in to reply
They have reformulated the question since I answered it, but now you would get it from "car starts accelerating at 4 m/s^2. As soon as the first car reaches a speed of 6 m/s". That takes 1.5 seconds. It was more obvious before.
In a velocity-time graph, distance covered equals area under the curve. The distance-time graph for two adjacent cars looks like this:
 The second car sets off at 1.5s (when the first car has reached 6m/s). The difference in distance travelled is the green area. This has a base of 1.5s and a height of 20m/s, so an area of 30m. Add on the initial separation of 2m to get 32m.
The second car sets off at 1.5s (when the first car has reached 6m/s). The difference in distance travelled is the green area. This has a base of 1.5s and a height of 20m/s, so an area of 30m. Add on the initial separation of 2m to get 32m.
You can do it in your head: Taking the position of the first car as the origin, the first car will reach x meters from the origin in t seconds. The second car will reach x − 2 meters from the origin in t + 1 . 5 seconds. So the distance between them will be 2 0 × 1 . 5 + 2 = 3 2 .
I forgot something. It works for t in which both cars are already at the constant velocity of 20 m/s.
Evaluate [ Assuming [ t ≥ 0 ∧ t ∈ R , ∫ 0 t ∫ 0 t ( { 4 0 ≤ x < 5 ) d x d t ] − ( Assuming [ t ≥ 0 ∧ t ∈ R , ∫ 0 t ∫ 0 t ( { 4 2 3 ≤ x < 5 + 2 3 ) d x d t ] − 2 ) ] /. t → 1 0 ⇒ 3 2
The car separations:
Assuming [ t ≥ 0 ∧ t ∈ R , ∫ 0 t ∫ 0 t ( { 4 0 ≤ x < 5 ) d x d t ] ⇒ { 2 t 2 1 0 ( 2 t − 5 ) 0 < t ≤ 5 t > 5
Assuming [ t ≥ 0 ∧ t ∈ R , ∫ 0 t ∫ 0 t ( { 4 2 3 ≤ x < 5 + 2 3 ) d x d t ] − 2 ⇒ ( { 2 0 ( t − 4 ) 2 1 ( 4 t 2 − 1 2 t + 9 ) t > 2 1 3 2 3 < t ≤ 2 1 3 ) − 2
FullSimplify [ 1 0 ( 2 t − 5 ) − ( 2 0 ( t − 4 ) − 2 ) ] ⇒ 3 2
I just guessed 2^5 = 32 Not sure that can be put to practice.
The first car accelerates to 6 m / s 2 at 1.5 sec. Then the second car drives. So it takes 1.5 sec for the second car to get to 2 0 m / s 2 after the first car gets there. That means the first car can drive another 1.5 seconds of 2 0 m / s . Which is 30 meters, plus the initial 2 meters, is 32 meters.
If the acceleration is 4m/sec^2, then the rate of acceleration is equal to 4t. the velocity at a time t would be 2t^2. The point where the first car reaches 6m/s would be where 6=2t^2, or 3^.5. this would give a distance at the terminal speed of 20m/s of approx 36.6 meters. the answer is not an integer, or 36 or 37 should be accepted. Or is acceleration really linear?
At an acceleration of 4 m / s 2 each car reaches a speed of 6 m / s after 1 . 5 s and a speed of 2 0 m / s after 5 s .
So we know the last car will drive for 5 s , the middle car will drive for 5 + 1 . 5 = 6 . 5 s , and the front car will drive 5 + 2 ( 1 . 5 ) = 8 s
To calculate distance D ( t ) = { ∫ 0 t 4 t = 2 t 2 2 0 x t ≤ 5 t > x
First car traveled 1 1 0 + 4 = 1 1 4 m ; second car traveled 8 0 + 2 = 8 2 m ; last car traveled 5 0 m
Δ between cars = 3 2 m
If the acceleration is 4m/sec^2, then the rate of acceleration is equal to 4t. the velocity at a time t would be 2t^2. The point where the first car reaches 6m/s would be where 6=2t^2, or 3^.5. this would give a distance at the terminal speed of 20m/s of approx 36.6 meters. the answer is not an integer, or 36 or 37 should be accepted. Or is acceleration really linear?
The question is easier if we calculate it backwards, start considering the last car.
Buy the time the rear car accelerates to 20m/s, the front car already accelerates to 20m/s 1.5 seconds ago (6/4=1.5s), and keep constant speed at 20m/s for 1.5s.
We don't need to care the positive acceleration part, because both cars moves for same distance during their acceleration. It doesn't affect their separation.
So final distance between them is just 20*1.5+2 = 32m, where the 2m is their initial separation.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
|
1 |
|
Relevant wiki: One Dimensional Kinematics: Motion Along a Straight Line
Let t = 0 when the first car begins to move, and t ⋆ is some time after the second car reaches the maximum speed.
During this time interval, the cars move in similar ways. The only differences are that the second car begins with 1 . 5 s standing still (waiting for the first car to move), and spending 1 . 5 s less time moving at the speed limit. Therefore the difference in distance traveled is Δ x = 1 . 5 s × 2 0 m / s = 3 0 m . Add this to the original 2 m between the cars, and you find the final distance to be 3 2 m .
For those who want to make a more detailed analysis:
t 0 1 . 5 5 . 0 6 . 5 v 1 0 6 2 0 2 0 v 2 0 0 1 4 2 0 x 1 0 4 . 5 5 0 8 0 x 2 − 2 − 2 2 2 . 5 4 8 Δ t 1 . 5 3 . 5 1 . 5 6 . 5 Δ v 1 6 1 4 0 2 0 Δ v 2 0 1 4 6 2 0 Δ x 1 4 . 5 4 5 . 5 3 0 8 0 Δ x 2 0 2 4 . 5 2 5 . 5 5 0