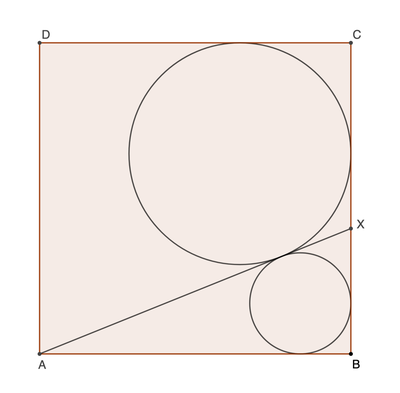
It's just circles and lines

In the figure, $K$ , $L$ are the centers of the circles, $KN\bot BC$ , $LT\bot BC$ , $LM\bot KN$ , $E$ is the common point of the two circles and $S$ is the common point of $AB$ and the circle with center $L$ .

We notice that $KM=KN-MN=R-r$ , $ML=NT=1-R-r$ , $AE=AS=1-r$ and $AK=AC-KC=\sqrt{2}-R\sqrt{2}$ .

Triangles $\triangle AKE$ and $\triangle KML$ are right triangles.

Using Pythagorean theorem on $\triangle KML$ ,

$\begin{aligned} K{{M}^{2}}+M{{L}^{2}}=K{{L}^{2}} & \Leftrightarrow {{\left( R-r \right)}^{2}}+{{\left( 1-R-r \right)}^{2}}={{\left( R+r \right)}^{2}} \\ & \Leftrightarrow {{R}^{2}}+{{r}^{2}}-2rR-2R-2r+1=0 \ \ \ \ \ (1)\\ \end{aligned}$ Using Pythagorean theorem on $\triangle AKE$ ,

$\begin{aligned} K{{E}^{2}}+A{{E}^{2}}=A{{K}^{2}} & \Leftrightarrow {{R}^{2}}+{{\left( 1-r \right)}^{2}}={{\left( \sqrt{2}-\sqrt{2}R \right)}^{2}} \\ & \Leftrightarrow {{R}^{2}}-{{r}^{2}}-4R+2r+1=0 \ \ \ \ \ (2) \\ \end{aligned}$

Subtracting $(2)$ from $(1)$ we get

$2{{r}^{2}}-2rR+2R-4r=0\Rightarrow R=\dfrac{{{r}^{2}}-2r}{r-1} \ \ \ \ \ (3)$ Substituting

$\begin{aligned} \left( 2 \right) & \overset{\left( 3 \right)}{\mathop{\Leftrightarrow }}\,{{\left( \dfrac{{{r}^{2}}-2r}{r-1} \right)}^{2}}-{{r}^{2}}-4\cdot \dfrac{{{r}^{2}}-2r}{r-1}+2r+1=0 \\ & \Leftrightarrow 4{{r}^{3}}-12{{r}^{2}}+8r-1=0 \\ & \Leftrightarrow r\approx 0.16243456\text{ or }r\approx 0.73040556\text{ or }r\approx 2.10715987 \\ \end{aligned}$ Obviously, $r$ is less than half the diagonal of the square, i.e. $r<\dfrac{\sqrt{2}}{2}\approx 0.707$ , hence $r\approx 0.16243456$ . For the answer, $\left\lfloor {{10}^{5}}r \right\rfloor =\boxed{16243}$ .

Let the radius of the larger circle be $R$ and denote the centers of the smaller and larger circle as $O_1$ and $O_2$ respectively. Also mark points $P$ and $Q$ on $BC$ such that $BP$ is tangent to the smaller circle at $P$ and $CQ$ is tangent to the larger circle at $Q$ . Note that the circles share a common point, say $T$ , on the segment $AX$ .

From the properties of tangents, $XP=XT=XQ=x$ Since $ABCD$ is a unit square, $BC=BX+CX=r+x+R+x=R+r+2x=1$ Constructing a perpendicular to $AB$ (parallel to $BC$ ), though point $O_1$ and let it intersect $O_2Q$ at $E$ . Clearly, $\triangle O_1EO_2$ is right angled at $E$ and has sides $O_1O_2=R+r$ , $O_1E=2x$ and $O_2E=R-r$ . By the Pythagorean theorem, $O_1E^2+O_2E^2=O_1O_2^2\implies (2x)^2+(R-r)^2=(R+r)^2\implies 4x^2=4Rr\implies x=\sqrt{Rr}$ Combining this with the previous relation, we have $R+r+2x=R+r+2\sqrt{Rr}=1\implies\sqrt{R}+\sqrt{r}=1$ Note that the circle centered at $O_1$ with radius $r$ is the incircle of $\triangle ABX$ . Using the formula for the inradius of a triangle, $\triangle=r\cdot s$ , $\frac{(r+x)(1)}{2}=r(1+x)\implies r+x=2r+2rx\implies x=\frac{r}{1-2r}$ Finally we have an equation in $r$ , $\sqrt{Rr}=(1-\sqrt{r})\sqrt{r}=\frac{r}{1-2r}$ Solving the above equation gives $\boxed{\lfloor{10^5r}\rfloor=16243}$

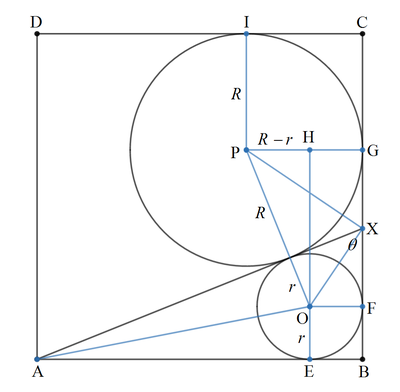
Let the centers of the small and large circles $O$ and $P$ , the radius of large circle be $R$ , and points $E$ , $F$ , $G$ , $H$ , and $I$ are feet of perpendicular. Consider $BC$ :

$\begin{aligned} BF + FG + GC & = BC \\ EO + OH + PI & = BC \\ r + \sqrt{(R+r)^2-(R-r)^2} + R & = 1 \\ r + 2\sqrt{Rr} + R & = 1 \\ (\sqrt R + \sqrt r)^2 & = 1 \\ \implies \sqrt R & = 1 - \sqrt r \end{aligned}$

Let $\angle AXB = \theta$ and consider $FG$ :

$\begin{aligned} FX + XG & = FG = OH \\ r \cot \frac \theta 2 + R \cot \left(90^\circ - \frac \theta 2\right) & = 2\sqrt{Rr} & \small \blue{\text{Let }t = \tan \frac \theta 2} \\ \frac rt + Rt & = 2\sqrt{Rr} & \small \blue{\text{Divide both sides by }\sqrt{Rr}} \\ \frac 1t \sqrt{\frac rR} + t \sqrt{\frac Rr} & = 2 \\ \sqrt{\frac r{Rt^2}} - 2 + \sqrt{\frac {Rt^2}r} & = 0 & \small \blue{\text{Let }\alpha^2 = \sqrt{\frac r{Rt^2}}} \\ \alpha^2 - 2 + \frac 1{\alpha^2} & = 0 \\ \left(\alpha - \frac 1\alpha \right)^2 & = 0 \\ \implies \alpha & = 1 \\ \implies \sqrt{\frac r{Rt^2}} & = 1 \\ \implies t & = \frac {\sqrt r}{1-\sqrt r} \end{aligned}$

Consider $AB$ :

$\begin{aligned} AE + EB & = AB \\ r \cot \frac {\angle XAB}2 + OF & = 1 \\ r\cot \left(45^\circ - \frac \theta 2\right) + r & = 1 \\ r \left(\frac {1+\blue t}{1-\blue t} \right) + r & = 1 & \small \blue{\text{Substitute }t = \frac {\sqrt r}{1-\sqrt r}} \\ \frac r{1-2\sqrt r} + r & = 1 \\ 2r\sqrt r - 2r - 2\sqrt r + 1 & = 0 \\ \implies r & \approx 0.162434565 \\ \implies \lfloor 10^5 r \rfloor & = \boxed{16243} \end{aligned}$

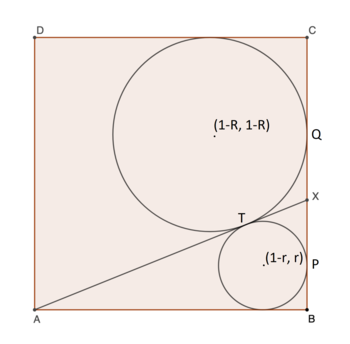
I solved using coordinate geometry. Let's take the origin at point $A$ . If the radius of the big circle is $R$ , and the radius of the small circle is $r$ , then the center of the big circle is $(1 - R, 1 - R)$ , and the center of the small circle is $(1 - r, r)$ . Also from the fact that tangents to a circle have the same length, it follows that segments $PX , TX, QX$ all have the same length, and since the side length of the square is $1$ , then that length is $\dfrac{1}{2} (1 - R - r )$ , hence point $X$ is $(1, \dfrac{1}{2} (1 + r - R) )$ . The first relation we can write is that of the distance between the centers of the two circles being equal to $R + r$ . Hence,

$(R + r)^2 = \Delta x^2 + \Delta y^2 = (R - r)^2 + (1 - R - r)^2$

The second equation expresses the fact the line segment joining the two centers is perpendicular to the tangent $AX$ , hence, has a slope that is the negative of the reciprocal of its slope:

$\dfrac{1 - R - r}{R - r} = \dfrac{-2}{1 + r - R }$

Simplifying the first equation yields,

$r^2 - R^2 - 2 r + 4 R - 1 = 0 \hspace{24pt}(1)$

The second equation becomes

$r^2 + R^2 - 2 R r - 2 r - 2 R + 1 = 0 \hspace{24pt}(2)$

Equations $(1) , (2)$ have three solutions for $(r, R)$ :

$1. \hspace{6pt} (0.162434565, 0.356371131)$

$2. \hspace{6pt} (2.107159872, 0.203947946)$

$3. \hspace{6pt} (0.730405564, 3.439680923)$

from which only the first one is valid while the other two are extraneous. Hence, the answer is $\lfloor 10^5 (0.162434565) \rfloor = \boxed{16243}$