It's Magic!
A magician holds one fair 6-sided die in his left hand and two in his right.
What is the probability that the number on the dice in his left hand is greater than the sum of the dice in his right?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
I don't understand this. This is what I did:
@Pi Han Goh , @David Vreken , @Chew-Seong Cheong, @Brilliant Mathematics , Please help!
Log in to reply
You're assuming that for k = 2 , 3 , … , 1 2 , the probability Pr [ sum of the two dice = k ] are equal, which is not true.
For example, Pr [ sum of the two dice = 2 ] = 6 1 × 6 1 ; whereas Pr [ sum of the two dice = 3 ] = 6 1 × 6 1 × 2
You can still use your spreadsheet but include the number of ways to get the RH value in each cell (for example, there's 1 way to get 2, 2 ways to get 3, 3 ways to 4, etc.). Then the "favourable" cells would add up to 20, the total would add up to 216, and the probability would be 20/216 = 5/54.
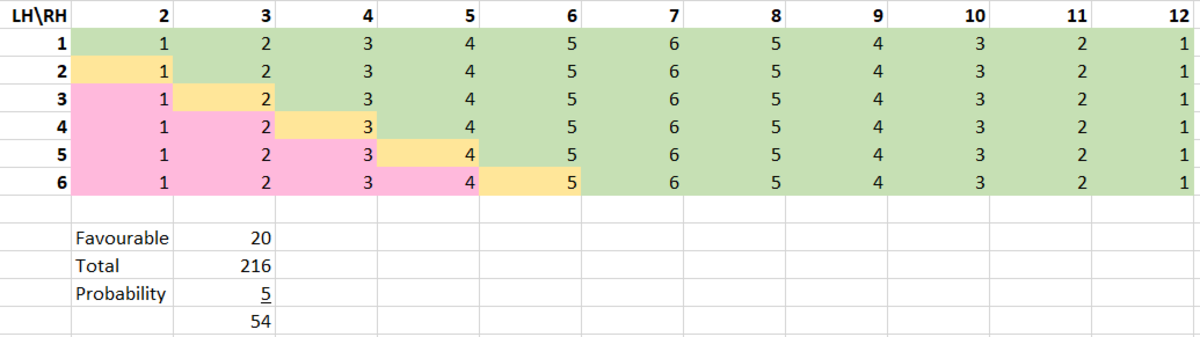
Total possible outcomes when rolling 3 dice = 6 3 = 216.
Observe that for the single die to be greater than the sum of the other two, the single die must be at least 3.
Single die : 3; Two other dice sum to be less than 3: [(1,1)] - 1 desired outcome
Single die : 4; Two other dice sum to be less than 4: [(1,1) (2,1) (1,2)] - 3 desired outcomes
Single die : 5; Two other dice sum to be less than 5: [(1,1) (2,1) (1,2) (3,1) (1,3) (2,2)] - 6 desired outcomes
Single die : 6; Two other dice sum to be less than 6: [(1,1) (2,1) (1,2) (3,1) (1,3) (2,2) (2,3) (3,2) (1,4) (4,1)] - 10 desired outcomes
Desired outcomes: 1 + 3 + 6 + 10 = 20
So the probability = 2 1 6 2 0 = 5 4 5