It's Mathematics Olympiad! - 3
For what values of the variable x does the inequality hold : ( 1 − 1 + 2 x ) 2 4 x 2 ≤ 2 x + 9 If a and b are minimum and maximum possible values of x , submit a + b .
S o u r c e : I n t e r n a t i o n a l M a t h e m a t i c s O l y m p i a d 1 9 6 0 P r o b l e m 2 (Not the real version of the question)
The answer is 5.125.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Since 1 + 2 x ≥ 0 , the minimum value of x is − 2 1 .
In order to eliminate the square root in the denominator, let x = 2 a 2 − 1 and x ≥ − 2 1 ⟹ a ≥ 0 .
So, we have, ( 1 − 1 + 2 ( 2 a 2 − 1 ) ) 2 4 ( 2 a 2 − 1 ) 2 ( 1 − a ) 2 ( a 2 − 1 ) 2 ( a + 1 ) 2 a 2 + 2 a + 1 a ∴ x ≤ 2 ( 2 a 2 − 1 ) + 9 ≤ a 2 + 8 ≤ a 2 + 8 ≤ a 2 + 8 ≤ 2 7 ≤ 2 ( 2 7 ) 2 − 1 = 8 4 5 Therefore, a = − 2 1 , b = 8 4 5 ⟹ a + b = 8 4 1
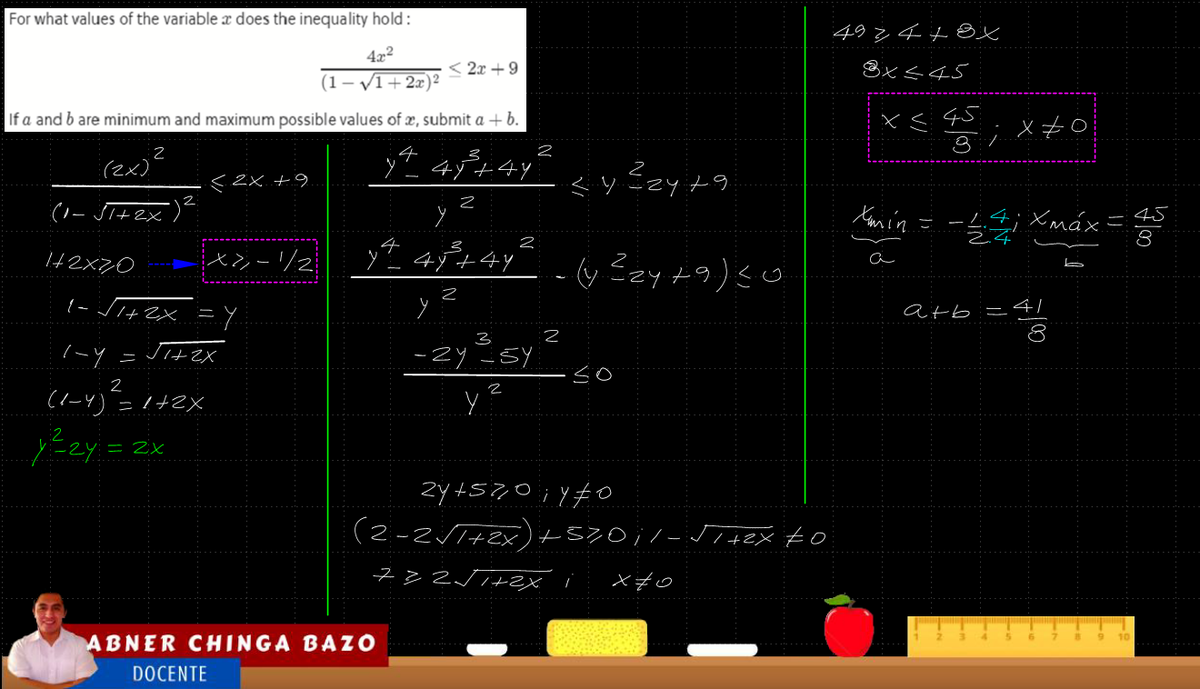
To solve this easily, rationalize LHS.
( 1 − 2 x + 1 ) 2 4 x 2 ⋅ ( 1 + 2 x + 1 ) 2 ( 1 + 2 x + 1 ) 2 ≤ 2 x + 9 ⟹ ( 1 + 2 x + 1 ) 2 ≤ 2 x + 9
Hence,
0 ≤ 2 x + 1 ≤ 2 7 ⟹ x ∈ [ − 2 1 , 8 4 5 ]